
Neural Network と数学は切っても切り離せないものですが、おそらくほとんどの人はそれが怖いのでしょう。 ディープラーニングについて、「これは私には理解できないほどの数学だ」、「本当にどれだけの企業がディープラーニングを使っているのだろう」といった怪しげな発言を耳にすることがあまりに多いのです。
でも、よく考えてみれば、それほど難しいことではありません。 私を信じてください。 アルゴリズムがなぜある動作をするのかを理解するには、舞台裏で何が起こっているのかを理解することが不可欠です。 複雑な機械学習アルゴリズムは、今日、私たちのために都合よくパッケージ化されており、関数を呼び出すだけで利用できます。 活性化関数の導関数は、あまり目立たない概念なので、私たちはしばしば無視しがちである。 しかし、強力なアルゴリズムの基礎となるものであり、理解するために少し余分に努力すれば、必ず報われる。
背景
Neural Network は、学習プロセスを触媒するために、隠れ層と出力層でさまざまな活性化関数を使用します。 一般的に使用される活性化関数には、Sigmoid および tanH 関数が含まれます。 最も人気のある活性化関数はReLU(Rectified Linear Unit)で、消失勾配の問題を効果的に克服することができるからです。 活性化関数の詳細については、また別の機会に紹介したいと思います。
なぜ活性化関数の微分が重要なのですか。
ご存知のように、ニューラルネットワークは2つのステップで駆動します。
シグモイド関数
シグモイド関数は S 字型の曲線を特徴とし、しばしばロジスティック関数の特殊ケースとして言及されます。 出力として確率を予測しなければならないような場合に最も有用である。
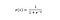
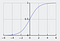
シグモイド関数は0と1の間にある値を出力します(確率を予測することを考えると当然です)。
シグモイド微分
この基本的な構成要素は、ニューラルネットワークを訓練するのに役立ち、次のような形式を取ります。


さっそくですが。 では、さっそく微分をやってみましょう。
アプローチ1

アプローチ2:
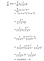
なぜ、このバージョンの派生物を使用するのでしょうか?
前方伝搬ステップでは、シグモイド関数 (σ(x)) を計算し、その値を手元に置いておきます。 バックプロパゲーションステップで導関数を計算するときに、上記の式にσ(x)の値を差し込むだけでOKです!
以上です!(`・ω・´) 読んでくれてありがとう!
。