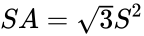学術雑誌については、Tetrahedron (journal)を参照。
| 正四面体 | |
|---|---|
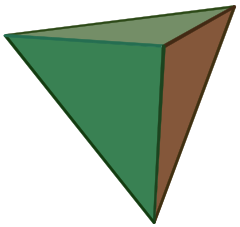 (回転モデルはこちら) |
|
| タイプ | プラトニック固体 |
| 要素 | |
| 辺による面 | 4{3} |
| シュレフリ記号 | {3,3}とs{2,2} |
| ワイゾフ記号 | 3 | 2 3 | 2 2 2 |
| コクサー-ダイニン | |
| 対称 | Td または (*332) |
| U01, C15, W1 | |
| 特性 | 正凸正三面体 |
| 二面角 | 70度。528779° = arccos(1/3) |
 3.3.3 (頂点図形) |
 Self-dual (dual polyhedron) |
 Net |
|
Tetrahedron (plural: tetrahedra) とは三角形の面4つで、3つがそれぞれの頂点を結んでできた多面体である。 正四面体は4つの三角形が正三角形であるもので、プラトニック立体の1つである。
四面体はピラミッドの1種であり、平たい多角形の底面と底面と共通点を結ぶ三角形の面を持つ多面体である。 四面体の場合、底面は三角形(4つの面のどれでも底面とみなすことができる)なので、四面体は三角ピラミッドやダイゴナルデルタ面体とも呼ばれる。
正四面体の公式
体積は
表面積は
Template.Templateを参照。Commonscat
- F. M. Jackson and Weisstein, Eric W., “Tetrahedron” from MathWorld.
- Weisstein, Eric W., “Tetrahedron” from MathWorld.
- Weisstein, Eric W., “Tetrahedron” from MathWorld.
- The Uniform Polyhedra
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Piero della Francesca’s formula for tetrahedron volume at MathPages
- Free paper models of a Tetrahedron and many other polyhedra
- An Amazing, 空間を埋め尽くす非正規の四面体。カレイドサイクルとして知られる「四面体の回転リング」の説明もあります。
- Tetrahedron Core Network 四面体構造を応用した弾力的な部分メッシュデータネットワーク
- 任意の四面体の慣性テンソルをその頂点座標で明示する厳密式
- The inertia tensor of a tetrahedron
Tetrahedron.The Uniform Polyhedra.The Tetrahedron, “Tetrahedron “From “Math World.Trial” from Math World.Trial インタラクティブな多面体モデル