El proporcional es sólo una forma de reaccionar ante un error en el sistema. El problema del control proporcional es que no puede detectar tendencias y ajustarse a ellas. Este es el trabajo del control integral.
Hay otra gráfica de ejemplo del error en un sistema a lo largo del tiempo a la izquierda de la figura 6. De nuevo, podría ser la distancia de un robot a un objeto, o podría ser el nivel de fluido en un tanque, o la temperatura en un horno de fábrica. Tal vez el objetivo que sigue el robot se aleja del mismo a una velocidad que el robot no alcanza. Puede que la junta de la puerta del horno esté desgastada o que la extracción de líquido del depósito sea inusualmente grande. Independientemente de la causa, como el control proporcional no está diseñado para reaccionar a las tendencias, no puede detectar y corregir el problema. Ahí es donde entra en escena el control integral.
El integral mide el área entre los valores de error y el eje de tiempo. Si el error no vuelve a cero, el área del error se hace cada vez más grande. El lado derecho de la Figura 6 muestra cómo la salida integral puede reaccionar a este tipo de tendencia. A medida que aumenta el área entre la curva de error y el eje del tiempo, la salida aumenta proporcionalmente a esta área. Como resultado, la salida impulsa al actuador cada vez más fuerte para corregir el error.
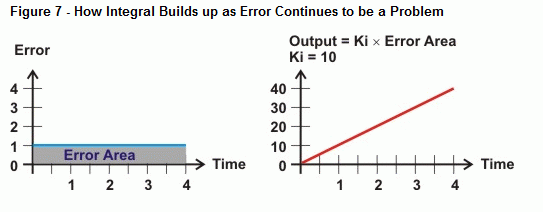
Entonces, ¿qué sucede cuando el error no es una línea recta, como la curva mostrada en la Figura 8? Eso es lo que determina la operación de cálculo de la integración, el área entre una curva y un eje. En el caso del control integral, a medida que pasa más tiempo con un error, el área bajo la curva crece, y también lo hace el valor que el cálculo integral utilizará para conducir contra el error del sistema. Si la curva de error cae por debajo del eje de tiempo, la acumulación de área negativa se resta de la acumulación de área positiva. Cuando se sintoniza correctamente, el control integral puede ayudar al sistema a afinar en un error de cero.
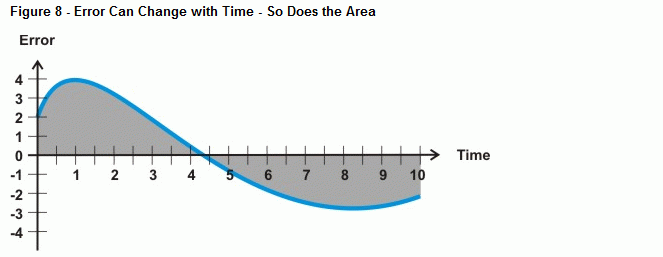
El BASIC Stamp puede aproximar el error bajo la curva con integración numérica. La figura 9 muestra cómo se puede aproximar el error bajo una curva sumando el área de un montón de pequeños rectángulos entre la curva de error y el eje del tiempo. El área de cada caja es el error multiplicado por el tiempo entre las mediciones. Sumando todas las áreas de las cajas, se obtiene una aproximación del área bajo la curva.
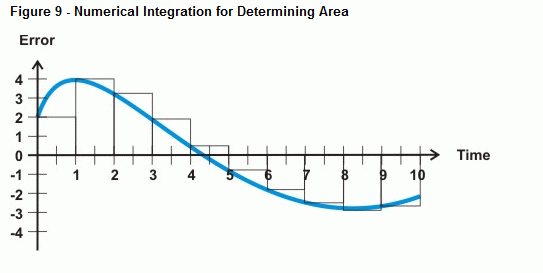
Si las mediciones están espaciadas uniformemente, se puede llamar a la anchura de cada caja un valor de 1. Esto hace que la matemática sea mucho más simple que tratar de tener en cuenta 20 ms entre las muestras, 5 minutos entre las muestras, o cualquiera que sea su tasa de muestreo. En lugar de multiplicar el error por el incremento de tiempo entre las muestras y luego añadir al siguiente error multiplicado por el tiempo, usted puede simplemente multiplicar cada muestra de error por un tiempo de 1. El resultado es que usted puede simplemente mantener un total continuo de las mediciones de error para su cálculo integral. Aquí hay un ejemplo de cómo hacer esto con PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
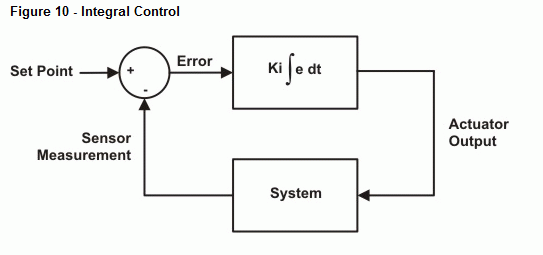
El siguiente programa de ejemplo realiza la integración numérica en la señal de error y ajusta la salida en consecuencia. Al igual que con el control proporcional, hay una constante que escala la salida de integración al valor deseado. Para simplificar, usaremos 10 de nuevo para Ki. La figura 10 muestra un diagrama de bloques del lazo de control. El término Kp ∫ edt se refiere a Kp multiplicado por la integral del error en el tiempo. En otras palabras, Kp multiplicado por el área acumulada entre la curva de error y el eje del tiempo.
Programa de ejemplo – IntegralAlgorithm.bs2
- Ingrese, guarde y ejecute IntegralAlgorithm.bs2.
- Ingrese esta secuencia de valores en el panel de la ventana de transmisión del Debug Terminal: 3 3 3 3 3 3 3 3 3. Observe cómo la salida de integral se hace más grande cada vez que se repite el 3. Ese es el trabajo de la integral, detectar tendencias y aumentar el impulso para corregirlo según sea necesario.
- Ahora prueba esta secuencia: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. El área bajo esta curva es 0 ya que el área negativa es igual al área positiva. Eso es también lo que el cálculo integral llegará cuando haya terminado de introducir la secuencia.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Cómo funciona IntegralAlgorithm.bs2
Este programa es un ProportionalAlgorithm.bs2 modificado para realizar el cálculo integral en su lugar. Ahora hay dos tipos diferentes de errores de los que hay que hacer un seguimiento, por lo que la matriz de variables de error se amplió a dos elementos. La variable error(0) registra el error actual, y error(1) registra el error acumulado. Las constantes Current CON 0 y Accumulator CON 1 hacen que la contabilidad sea un poco más sensata con error(current) y error(accumulator).
El otro cambio que se hizo es que el error se acumula y la salida integral se calcula con estas dos sentencias:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Tu turno – Sujetando la salida integral
Como te habrás dado cuenta al introducir repetidamente 3 en la Terminal de Depuración, la salida de la unidad integral puede realmente empezar a escaparse. Puede utilizar los operadores MIN y MAX para evitar que el control integral se exceda con la salida. Repitamos la actividad de offset del servo y limitemos la salida de 650 a 850.
- Cambia la sentencia drive = i por drive = i + Offset MIN 650 MAX 850.
- Ejecuta el programa y verifica que la salida integral se limita a valores entre 650 y 850. Pruebe a introducir repetidamente 2 y luego -2.