Curentul alternativ, sau curent alternativ, este numit astfel deoarece curentul alternează sau se întoarce și se întoarce între două polarități. Cu alte cuvinte, curentul (și, în consecință, tensiunea) este o funcție a timpului. Acest lucru este fundamental diferit de curentul continuu, care este fix în polaritate și, în general, constant în timp. O sursă de tensiune continuă de laborator, de exemplu, menține în mod ideal o tensiune fixă la bornele sale și nu variază în timp. În schimb, pe măsură ce o formă de undă de curent alternativ se balansează înainte și înapoi în timp, forma sa poate prezenta variații largi, variind de la traseele simple și regulate ale standardelor de laborator, cum ar fi undele sinusoidale, undele triunghiulare și undele pătrate, până la formele de undă mult mai complexe și ondulatorii produse de instrumentele muzicale și de vocea umană.
Unda sinusoidală este cea mai simplă undă care poate fi creată. Ea reprezintă mișcarea unui vector simplu care se rotește cu o viteză constantă, cum ar fi deplasarea verticală a acului secundar al unui ceas. Un exemplu este prezentat în figura \(\PageIndex{1}\). Pe axa orizontală este reprezentat timpul. Aceasta crește pe măsură ce ne deplasăm de la stânga la dreapta (de exemplu, dacă punctul A se află la dreapta punctului B, atunci A apare mai târziu în timp decât B). Axa verticală este reprezentată aici în general ca un procent din maxim, dar în mod normal ar fi o măsură de tensiune, curent, presiune acustică sau altele asemenea.
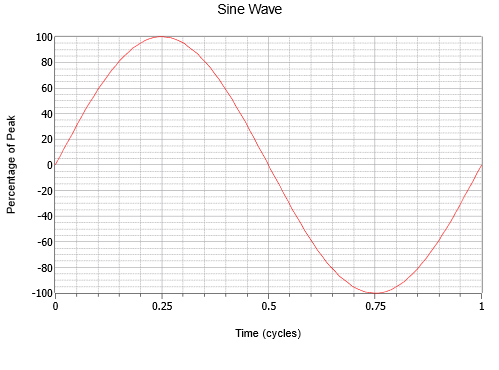
Figura \(\PageIndex{1}\): O undă sinusoidală.
Observați variația lină care începe de la zero, crește până la un vârf pozitiv la un sfert din parcurs, scade înapoi la zero la jumătatea parcursului, continuă până la un vârf negativ la trei sferturi din parcurs și apoi crește din nou până unde a început. Acest proces se repetă apoi. Fiecare repetare se numește ciclu. În figura \(\PageIndex{1}\), este prezentat un ciclu complet.
Undele sinusoidale prezintă simetrie de sfert de undă. Adică, fiecare sfert (în timp) al undei este identic cu oricare altul dacă pur și simplu îl întoarceți în jurul axei orizontale și/sau îl rotiți în poziție verticală în jurul vârfului său. Timpul necesar pentru a parcurge un ciclu se numește perioadă și este notat cu simbolul \(T\) (pentru Timp). Reciprocul perioadei este frecvența, \(f\).
\
Frecvența indică câte cicluri există într-o secundă. Pentru a-l onora pe unul dintre cercetătorii din secolul al XIX-lea în acest domeniu, în loc să numim unitatea „cicluri pe secundă”, folosim Hertz, numit după Heinrich Hertz și prescurtat Hz. În figura \(\(\PageIndex{2}\) sunt reprezentate trei unde sinusoidale cu frecvențe diferite; unda inițială (verde), o undă la o frecvență dublă (albastru) și o a treia la jumătate din frecvență sau la o perioadă dublă (roșu).
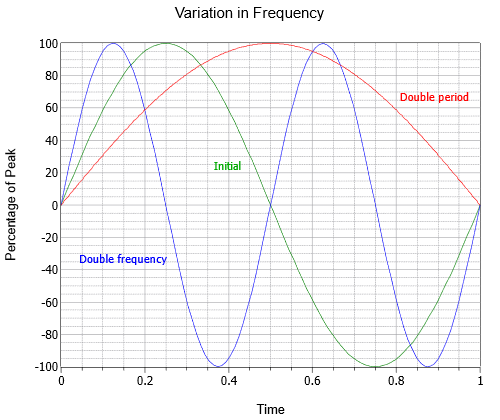
Figura \(\PageIndex{2}\): Variația frecvenței undei sinusoidale.
Amplitudinea (verticală) undei poate fi exprimată ca o mărime de vârf, care reprezintă variația de la linia zero centrală până la valoarea cea mai pozitivă. Amplitudinea poate fi exprimată, de asemenea, ca valoare de la vârf la vârf; distanța de la valoarea cea mai negativă la cea mai pozitivă. Pentru o undă sinusoidală, aceasta va fi întotdeauna de două ori valoarea de vârf, deși s-ar putea să nu fie cazul pentru alte unde care pot fi asimetrice. O serie de trei unde sinusoidale cu amplitudini diferite este prezentată în figura \(\PageIndex{3}\). Alături de cea inițială (verde) sunt versiunile de amplitudine dublă (albastru) și de jumătate de amplitudine (roșu).
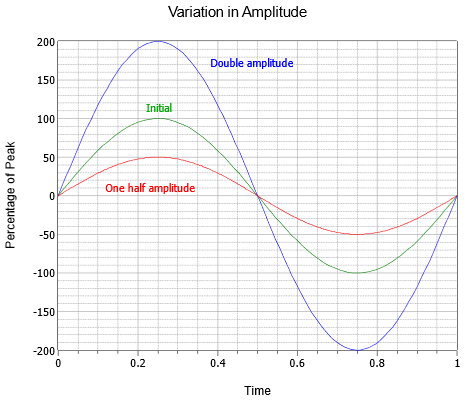
Figura \(\PageIndex{3}\): Variația amplitudinii undei sinusoidale.
Combinând acești parametri, considerați forma de undă de tensiune prezentată în figura \(\PageIndex{4}\). Aici vedem două cicluri ale unei forme de undă de tensiune alternativă.
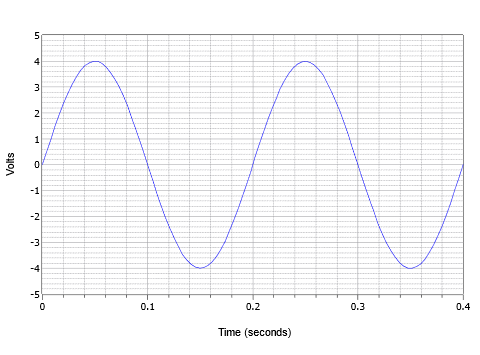
Figura \(\PageIndex{4}\): Exemplu de undă sinusoidală de bază.
Valoarea de vârf este de 4 volți, iar valoarea de vârf la vârf este de 8 volți (abreviată de obicei ca „8 V pp”). Perioada unui ciclu este de 0,2 secunde, sau \(T = 200\) milisecunde. Mai mult, frecvența, \(f = 1/200\) milisecunde, sau 5 Hz (5 cicluri într-o secundă).
Formele de undă CA pot fi, de asemenea, combinate cu un decalaj de curent continuu. Adăugarea unui nivel pozitiv de curent continuu deplasează unda în sus pe verticală, în timp ce un nivel negativ de curent continuu deplasează unda în jos pe verticală. Acest lucru nu modifică frecvența sau porțiunea de curent alternativ a amplitudinii (deși vârfurile absolute s-ar deplasa cu valoarea de curent continuu). Figura \(\PageIndex{5}\) arată efectul diferitelor decalaje de curent continuu. Deasupra undei inițiale (verde) se află o undă de altfel identică cu un decalaj pozitiv de curent continuu egal cu 20% din valoarea de vârf originală (albastru). Sub unda originală se află o a treia undă (roșie) care prezintă un decalaj negativ de curent continuu egal cu jumătate din valoarea de vârf a undei originale.
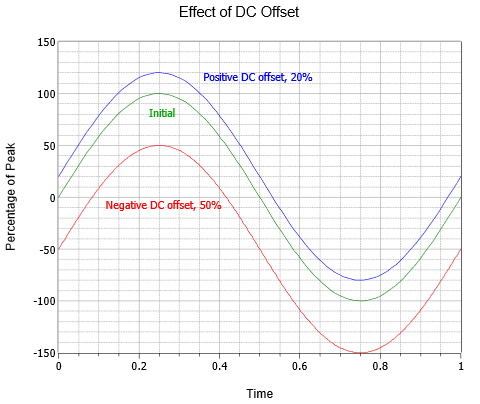
Figura \(\PageIndex{5}\): Variația decalajului DC al undei sinusoidale.
În plus, este posibil ca o undă sinusoidală să fie decalată în timp în comparație cu o altă undă sinusoidală sau cu o referință. Deși este posibil să se indice această deplasare ca timp absolut, este mai frecvent să se facă acest lucru ca o deplasare de fază, adică timpul exprimat ca o parte a perioadei în grade. De exemplu, dacă o sinusoidă este înaintea alteia cu un sfert din perioadă, se spune că este în avans cu 90\(^{\circ}\) (adică 1/4 din 360\(^{\circ}\)). Dacă este în urmă cu ½ din perioadă, se spune că este în urmă cu 180\(^{\circ}\) (adică mai târziu în timp cu 1/2 ciclu). Un alt mod de a afirma acest lucru este că formele de undă anterioare încep mai devreme în timp și astfel sunt desenate la stânga referinței, în timp ce formele de undă întârziate încep mai târziu în timp și sunt desenate la dreapta.
Figura \(\PageIndex{6}\) ilustrează efectul defazajului. Observați că în acest grafic, \(t = 0\) a fost mutat în centrul axei orizontale. Curba din mijloc reprezintă unda inițială, sau de referință (verde). În stânga (roșu) este o undă care precede unda inițială cu o optime de ciclu, sau 45\(^{\circ}\). În dreapta (albastru), este o undă întârziată cu jumătate de ciclu, sau -22,5\(^{\circ}\).
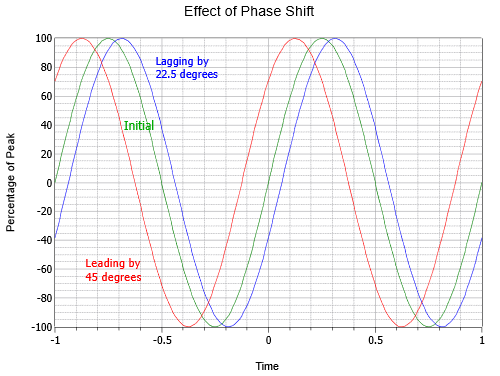
Figura \(\PageIndex{6}\): Variația de fază a undei sinusoidale.
Combinarea elementelor de mai sus ne permite să dezvoltăm un format general pentru o undă sinusoidală (tensiune prezentată):
\
Unde
\(v(t)\) este tensiunea la un anumit moment \(t\),
\(V_{DC}\) este decalajul de curent continuu, dacă există,
\(V_{P}\) este valoarea de vârf,
\(f\) este frecvența,
\(\theta\) este defazajul (+ dacă este în față și trasată spre stânga, – dacă este în urmă și trasată spre dreapta).
Pentru un exemplu rapid și practic, forma de undă prezentată în figura \(\PageIndex{4}\) are o amplitudine de 4 volți de vârf, o frecvență de 5 Hz și nici un decalaj de curent continuu sau defazaj. Astfel, expresia sa este \(v(t) = 4 \sin (2 \pi 5 t)\)
Pentru a calcula o deplasare de fază, determinați mai întâi diferența de timp dintre forma de undă și referință, pe care o vom numi \(\Delta t\). Referința poate fi un punct fix în timp (de exemplu, \(t = 0\)) sau o altă formă de undă. În general, modul simplu de a face acest lucru este de a măsura diferența la trecerile pe zero, presupunând că nu există un decalaj de curent continuu. Dacă există un decalaj, efectuați măsurarea în locul în care a fost deplasată trecerea la zero (de exemplu, la nivelul decalajului de curent continuu). Odată găsită diferența, împărțiți-o la perioadă pentru a reprezenta decalajul ca o fracțiune de perioadă. Deoarece un ciclu reprezintă o rotație a vectorului, sau 360 de grade, înmulțiți pur și simplu fracția cu 360 de grade pentru a afla defazajul în grade. Exprimat sub forma unei formule:
\
Rețineți, dacă unda este decalată spre stânga, atunci este în față și pozitivă, în timp ce o decalare spre dreapta este întârziată sau întârziată în timp și, prin urmare, negativă.
Exemplu \(\PageIndex{1}\)
Scrieți expresia pentru forma de undă prezentată în figura \(\PageIndex{7}\).
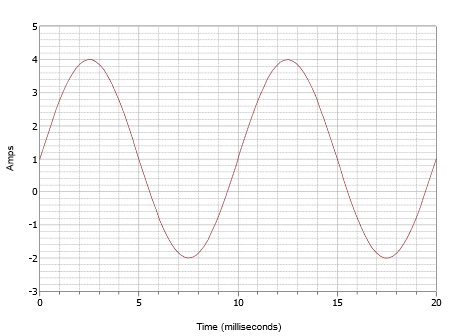
Figura \(\PageIndex{7}\): Forma de undă pentru exemplul \(\PageIndex{1}\).
Această formă de undă poate arăta superficial ca cea din figura \(\PageIndex{4}\) dar nu vă lăsați păcăliți de acest lucru. În primul rând, scara de timp este diferită. Pentru această formă de undă, un ciclu se termină în 10 milisecunde. Prin urmare, frecvența este
\
\
\
A doua problemă este decalajul DC. Observați că vârful pozitiv apare la 4 amperi, în timp ce vârful negativ apare la -2 amperi. Acest lucru indică o valoare de vârf la vârf de 6 amperi. Fără un offset, vârful pozitiv ar fi la 3 amperi, prin urmare există un offset DC de +1 amper. Centrul vertical al formei de undă este deplasat în sus de la 0 amperi la +1 amperi. Acest punct se află la t = 0, prin urmare, nu există defazaj. Expresia rezultată este:
\
Exemplu \(\PageIndex{2}\)
Scrieți expresia pentru forma de undă prezentată în Figura \(\PageIndex{8}\).
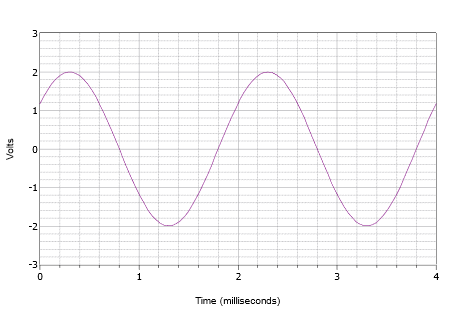
Figura \(\PageIndex{8}\): Forma de undă pentru exemplul \(\PageIndex{2}\).
În primul rând, vârful pozitiv este de 2 volți, iar valoarea de vârf la vârf este de 4 volți. Prin urmare, nu există niciun decalaj DC. Centrul vertical al undei nu începe la \(t = 0\), deci trebuie să existe un defazaj. Valoarea la \(t = 0\) este de 1,2 volți. Unda atinge aceeași amplitudine la \(t = 2\) milisecunde și începe să repete un alt ciclu. În consecință, perioada trebuie să fie de 2 milisecunde. Frecvența este reciproca acestei valori, și deci \(f = 500\) Hz.
Forma de undă este deplasată spre stânga, ceea ce indică o defazaj pozitiv sau de conducere. Dacă examinăm al doilea ciclu, vedem că atinge zero volți la 1,8 milisecunde. Prin urmare, deplasarea este de 0,2 milisecunde. Exprimată în grade, aceasta este:
\
\
\
Expresia finală este:
\
Exemplu \(\PageIndex{3}\)
Desenați forma de undă corespunzătoare expresiei următoare.
\
În primul rând, observați că decalajul de -3 volți împinge vârful pozitiv în jos de la 5 volți la 2 volți, iar vârful negativ în jos de la -5 volți la -8 volți. Frecvența de 40 kHz dictează o perioadă de:
\
\
\
Deplasarea de fază de -72\(^{\circ}\) reprezintă 72/360, sau 0,2 cicluri. Aceasta corespunde unei întârzieri în timp (decalată spre dreapta, deoarece este negativă) de 0,2 ori 25 \(\mu\)s, sau 5 \(\mu\)s.
Începând, este adesea mai bine să construiți graficul printr-o serie de pași discreți decât să încercați să desenați totul dintr-o singură dată. Mai întâi, desenați o undă sinusoidală cu o amplitudine de vârf de 5 volți și o perioadă de 25 \(\mu\)s. Acum, împingeți forma de undă cu 3 volți în jos, astfel încât vârful pozitiv să fie de numai 2 volți, iar vârful negativ să fie la -8 volți. În cele din urmă, împingeți forma de undă nou decalată spre dreapta cu 5 \(\mu\)s. Rezultatul este prezentat în figura \(\PageIndex{9}\).
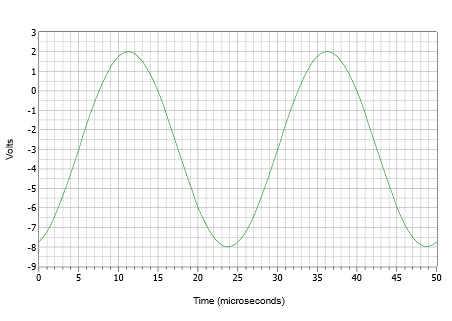
Figura \(\PageIndex{9}\): Forma de undă pentru exemplul \(\PageIndex{3}\).
1.2.1: Măsurători de laborator
În laborator, un generator de funcții este utilizat pentru a genera sinusuri și alte forme de undă. Aceste dispozitive vor permite un control precis atât asupra amplitudinii, cât și asupra frecvenței undei, împreună cu adăugarea unui offset de curent continuu, dacă se dorește. Un exemplu este prezentat în figura \(\PageIndex{10}\). Instrumentul de măsurare corespunzător este osciloscopul, sau doar osciloscopul, pe scurt.

Figura \(\PageIndex{10}\): Generator de semnal de laborator.
Osciloscopul este probabil cel mai util și versatil dispozitiv de măsurare din laborator. În mod obișnuit, acestea dispun de două sau patru canale de intrare, deși sunt posibile mai multe. Fiecare canal de intrare are propria ajustare a sensibilității și toate canalele au o referință de timp comună. Afișajul desenează formele de undă în același mod ca cele observate în figurile \(\PageIndex{1}\) – \(\PageIndex{9}\). De asemenea, pot trasa o tensiune față de alta (modul X – Y). Osciloscoapele moderne au caracteristici suplimentare, cum ar fi măsurarea automată a frecvenței, amplitudinii, defazajului etc., măsurători bazate pe cursor și posibilitatea de a salva imaginile afișate ca fișiere grafice. Un exemplu de osciloscop digital cu patru canale este prezentat în figura \(\PageIndex{11}\).

Figura \(\PageIndex{11}\): Un osciloscop digital.
1.2.2: Simboluri schematice
În ceea ce privește schemele, simbolurile pentru sursele de tensiune și curent alternativ sunt prezentate în figura \(\PageIndex{12}\). Marcajele de polaritate și direcție nu sunt absolute; la urma urmei, acestea sunt surse de curent alternativ a căror polaritate și direcții se schimbă înainte și înapoi. În schimb, marcajele sunt folosite pentru a stabili o referință de sincronizare, în special în circuitele care utilizează surse multiple.
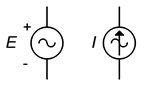
Figura \(\PageIndex{12}\): Simboluri schematice pentru sursa de tensiune de curent alternativ (stânga) și sursa de curent (dreapta).
Merită să ne amintim că negarea unei surse este același lucru cu inversarea polarității acesteia. Acest lucru era valabil pentru sursele de curent continuu și rămâne valabil pentru sursele de curent alternativ. Acest lucru este ilustrat în figura \(\PageIndex{13}\). Uneori, inversarea sau negarea sursei va face ca analiza să fie puțin mai evidentă sau mai ușor de vizualizat.
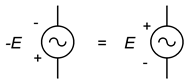
Figura \(\PageIndex{13}\): Echivalența polaritate/semnătură.
Exemplu \(\PageIndex{4}\)
Să presupunem că un osciloscop afișează două unde așa cum este descris în figura \(\PageIndex{14}\). Determinați defazajul formei de undă mai mică cu vârf de 20 de volți (albastru) în raport cu forma de undă mai mare cu vârf de 25 de volți (roșu).
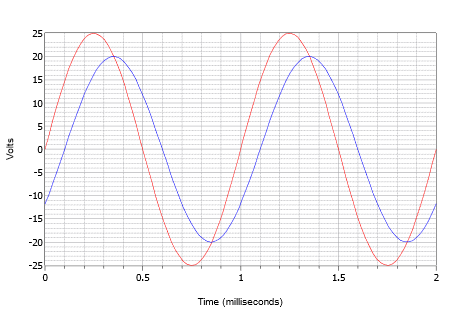
Figura \(\PageIndex{14}\): Formele de undă pentru exemplul \(\PageIndex{4}\).
În primul rând, observați că niciuna dintre unde nu prezintă un decalaj de curent continuu. Dacă una sau ambele ar avea un decalaj, unda (undele) ar trebui să fie deplasată (deplasate) pe verticală pentru ca punctele lor normale de trecere pe zero să fie la același nivel. Măsurând oricare dintre unde, se constată că perioada este de 1 milisecundă. Deplasarea temporală poate fi găsită cel mai ușor la oricare dintre punctele de trecere la zero (există patru locații din care se poate alege). Întârzierea este o abatere mică, sau 0,1 milisecunde, undele mai mici fiind întârziate în timp, sau întârziate față de unda mai mare. Acest lucru indică o defazaj negativ.
\
\
\
1.2.3: Sine și cosinusuri
Există o mână de defazaje specifice care merită o privire mai atentă. Dacă o undă sinusoidală este inversată, adică răsturnată cu susul în jos, nu se poate distinge de o undă sinusoidală care a fost decalată fie cu +180, fie cu -180 grade. Cu alte cuvinte, o astfel de undă poate fi scrisă în trei moduri diferite: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\), sau \(\sin (2 \pi ft + 180^{\circ})\). În plus, dacă o undă sinusoidală este decalată cu +90 de grade (adică înainte și la stânga), aceasta poate fi denumită și undă cosinusoidală. Astfel, \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). În cele din urmă, dacă o undă sinusoidală este decalată cu -90 de grade (adică întârziată și la dreapta), aceasta poate fi numită undă cosinusoidală negativă sau inversată. Astfel, \(\sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). Relațiile dintre aceste patru unde sunt ilustrate în figura \(\PageIndex{15}\).
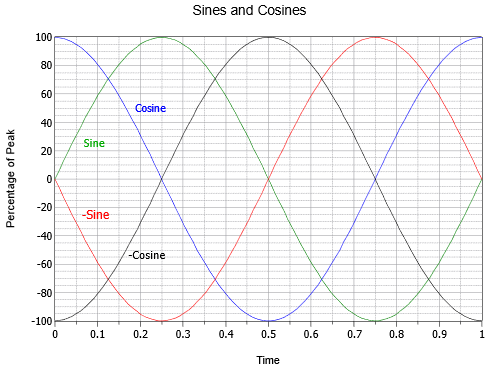
Figura \(\PageIndex{15}\): Relații temporale între sinusuri și cosinusuri.
De asemenea, este de remarcat faptul că unda cosinus reprezintă prima derivată, sau panta, a undei sinusoidale. După cum probabil vă amintiți din alte studii, panta sau „abruptul” unei drepte reprezintă raportul dintre variația verticală și variația orizontală, numită uneori „creșterea față de cursă”. În cazul unei tensiuni, ar fi variația tensiunii în raport cu variația în timp, sau \(\Delta V/ \Delta t\). Pentru o curbă netedă, în continuă schimbare, cum ar fi o undă sinusoidală, panta la un anumit punct este definită în mod corespunzător ca fiind prima derivată, sau \(dv/dt\) în acest caz. Pentru a verifica vizual că acest lucru este adevărat, observați că partea cea mai abruptă a undei sinusoidale (verde) se află acolo unde aceasta traversează amplitudinea zero. Pe măsură ce traversează zero în timp ce se deplasează pozitiv [la \(t = 0\) sau \(t = 1\) în figura \(\PageIndex{15}\)]), cosinusul (albastru) se află la vârful său pozitiv. Pe măsură ce sinusul trece prin zero în timp ce se deplasează în sens negativ (la \(t = 0,5\)), cosinusul se află la vârful său negativ. Mai mult, sinusoidul este plat, cu o pantă de zero la vârfurile sale pozitive și negative (la \(t = 0,25\\) și, respectiv, \(t = 0,75\)), iar în acele momente amplitudinea cosinusului este, de asemenea, zero. De asemenea, este adevărat că unda sinusoidală este panta undei cosinusoidale negative, cosinusul negativ este panta sinusului negativ, iar sinusul negativ este panta cosinusului. Mergând în sens invers, putem spune că antiderivata (integrala nedeterminată) unei unde cosinusoidale este o undă sinusoidală, integrala unei unde sinusoidale este o undă cosinusoidală negativă, și așa mai departe. Aceste relații se vor dovedi foarte utile atunci când ne vom îndrepta atenția asupra răspunsului condensatoarelor și inductorilor în circuitele de curent alternativ.
1.2.4: Măsurarea RMS – Root Mean Square
Pe lângă vârf și vârf la vârf, amplitudinea poate fi dată ca o valoare RMS (Root Mean Square). De fapt, în cazul în care nu se specifică vârful sau vârful la vârf, se presupune că măsurarea este RMS. RMS este un calcul special utilizat pentru a găsi puterea echivalentă în curent continuu (foarte frecvent, de exemplu, în cazul amplificatoarelor de putere audio). Cu alte cuvinte, dacă ne interesează să aflăm puterea într-o rezistență, calculul trebuie efectuat utilizând valorile RMS pentru tensiune sau curent, nu valorile de vârf sau vârf-la-vârf. În caz contrar, se vor obține puteri eronate. Acest lucru este valabil indiferent de forma de undă; fie că este vorba de o undă sinusoidală, de o undă triunghiulară sau de undele complexe ale semnalelor muzicale. Dacă o tensiune este specificată ca RMS, aceasta poate fi tratată pentru calculele de putere la fel ca o tensiune de curent continuu de mărime echivalentă. De exemplu, o sinusoidală RMS de 1 volt va produce aceeași disipare de putere și încălzire într-un rezistor dat ca și 1 volt CC. Din acest motiv, RMS este uneori denumită valoarea efectivă (adică valoarea efectivă de curent continuu).
Numele de root-mean-square descrie procesul de determinare a valorii efective. În primul rând, amintiți-vă că puterea este proporțională cu pătratul tensiunii sau curentului. Astfel, primul nostru pas va fi să ridicăm la pătrat forma de undă de intrare. Desigur, forma de undă este o funcție de timp și pătratul acesteia va produce o nouă formă. În acest moment, trebuie să găsim valoarea medie a acestei noi forme. Motivul pentru aceasta este simplu, dar nu neapărat evident. Componentele electrice și electronice au masă și, prin urmare, nu se încălzesc sau se răcesc instantaneu. Ele prezintă o constantă de timp termică. Prin urmare, ele răspund la o intrare medie în timp. Deși am putea calcula un fel de „putere de vârf instantanee” la un anumit moment în timp, aceasta nu reprezintă puterea echivalentă în curent continuu. Odată ce am obținut valoarea medie a acestei forme de undă la pătrat, valoarea corespunzătoare de curent continuu este doar rădăcina pătrată a mediei. Rezultatul este o valoare fracționară între zero și unu care este utilizată ca factor de scalare pentru a transforma o valoare de vârf într-o valoare RMS. Valoarea va fi unică pentru forma de undă specifică. Adică, toate sinusurile (indiferent de fază) au același factor, toate undele triunghiulare regulate au același factor și așa mai departe. Deoarece ne ocupăm în principal de sinusuri, să analizăm mai îndeaproape determinarea factorului RMS pentru acestea.
Începem cu expresia de bază pentru o undă sinusoidală fără decalaj de curent continuu sau defazaj și cu o amplitudine de unu:
\
Primul pas este să ridicăm la pătrat această formă de undă. O identitate trigonometrică utilă este
\
Aplicând-o la unda noastră rezultă:
\
Această expresie descrie o undă cosinusoidală inversată la o frecvență dublă față de cea originală și la jumătate din amplitudinea originală, călătorind pe un decalaj de curent continuu egal cu valoarea sa de vârf. Cu alte cuvinte, vârful negativ al cosinusului este la zero, iar vârful pozitiv este la 1. Următorul pas este de a găsi valoarea medie sau medie a acestui rezultat intermediar. Media este egală cu decalajul de 0,5. Acest lucru poate fi vizualizat ca fiind zona de deasupra decalajului care umple perfect „depresiunea” de sub decalaj. Pasul final constă în calcularea rădăcinii pătrate a mediei. Rădăcina pătrată a lui 0,5 este egală cu unu peste rădăcina pătrată a lui doi, adică aproximativ 0,707. Prin urmare, valoarea RMS este de 0,707 ori valoarea de vârf. Alternativ, ați putea împărți vârful la rădăcina pătrată de doi, adică aproximativ 1,414. Acest proces este prezentat grafic în figura \(\PageIndex{16}\).
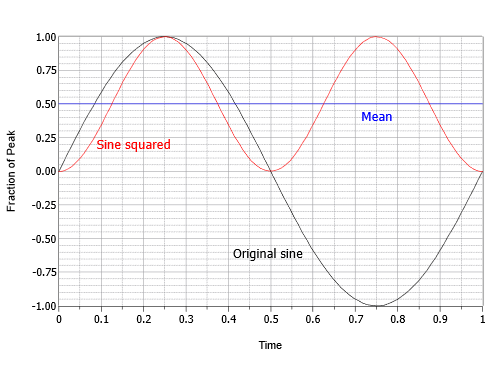
Figura \(\PageIndex{16}\): Proces pentru a găsi factorul RMS pentru sinusuri.
În rezumat, pentru undele sinusoidale, RMS este întotdeauna valoarea de vârf înmulțită cu 0,707. Am putea spune, de asemenea, că valoarea RMS a oricărei unde sinusoidale este vârful său împărțit la aproximativ 1,414. Din nou, aceste raporturi nu ar fi neapărat valabile pentru undele non-sinusoidale. Detalii privind alte forme comune pot fi găsite în Anexa C. În cele din urmă, raportul dintre valoarea de vârf și valoarea RMS se numește raportul de creastă. Aceasta este o valoare fixă pentru undele sinusoidale (din nou, aproximativ 1,414), dar poate fi de peste 10:1 pentru unele tipuri de semnale audio.
1.2.5: Lungimea de undă
Un alt element de interes este viteza de propagare a undei. Aceasta variază foarte mult. În cazul luminii în vid (sau, cu o aproximație apropiată, al unui curent electric într-un fir), viteza este de aproximativ 3E8 metri pe secundă (adică 300.000 km/s) sau aproximativ 186.000 mile pe secundă.
Dată o viteză și o perioadă, ne putem imagina la ce distanță sunt vârfurile undei. Această distanță se numește lungime de undă și este notată cu litera greacă lambda \(\lambda\). Lungimea de undă este egală cu viteza împărțită la frecvență, \(\lambda = v/f\). Astfel, pentru un difuzor care produce un sunet sinusoidal de 100 Hz, deoarece viteza sunetului în aer este de 344 m/s, atunci \(\lambda = 344 m/s \, / \, 100\) Hz, sau 3,44 metri (puțin peste 11 picioare). Observați că, cu cât frecvența este mai mare, cu atât lungimea de undă este mai scurtă. De asemenea, observați că, cu cât viteza este mai mare, cu atât lungimea de undă este mai mare. Calculele privind lungimea de undă au o importanță deosebită în domeniul telecomunicațiilor și al acusticii.
.