Ce este Python SciPy și cum se utilizează?

Matematica se ocupă de un număr foarte mare de concepte care sunt foarte importante, dar, în același timp, complexe și consumatoare de timp. Cu toate acestea, Python pune la dispoziție biblioteca SciPy cu drepturi depline care ne rezolvă această problemă. În acest tutorial SciPy, veți învăța cum să folosiți această bibliotecă împreună cu câteva funcții și exemplele lor.

Înainte de a trece mai departe, aruncați o privire la toate subiectele discutate în acest articol:

• Ce este SciPy?
• NumPy vs SciPy
• Subpachete în SciPy
• Funcții de bază
• Funcții speciale
• Funcții de integrare
• Funcții de optimizare
• Funcții de transformare Fourier
• Semnale Funcții de procesare a semnalelor
• Algebră liniară
• Valori proprii disparate
• Structuri de date și algoritmi spațiali
• Funcții de procesare a imaginilor multidimensionale
• File IO

Să începem deci. 🙂

SciPy este o bibliotecă Python open-source care este folosită pentru a rezolva probleme științifice și matematice. Este construită pe extensia NumPy și permite utilizatorului să manipuleze și să vizualizeze date cu o gamă largă de comenzi de nivel înalt. După cum s-a menționat anterior, SciPy se bazează pe NumPy și, prin urmare, dacă importați SciPy, nu este nevoie să importați NumPy.

NumPy vs SciPy

Atât NumPy, cât și SciPy sunt biblioteci Python utilizate pentru analize matematice și numerice utilizate. NumPy conține date de matrice și operații de bază, cum ar fi sortarea, indexarea etc., în timp ce SciPy constă în tot codul numeric. Deși NumPy oferă o serie de funcții care pot ajuta la rezolvarea problemelor de algebră liniară, transformări Fourier etc., SciPy este biblioteca care conține, de fapt, versiuni complet echipate ale acestor funcții împreună cu multe altele. Cu toate acestea, dacă faceți analiză științifică folosind Python, va trebui să instalați atât NumPy, cât și SciPy, deoarece SciPy se bazează pe NumPy.

Subpachete în SciPy:

SciPy are un număr de subpachete pentru diverse calcule științifice care sunt prezentate în tabelul următor:

Cu toate acestea, pentru o descriere detaliată, puteți urmări documentația oficială.

Aceste pachete trebuie să fie importate exclusiv înainte de a le utiliza. De exemplu:

from scipy import cluster

Înainte de a analiza în detaliu fiecare dintre aceste funcții, să aruncăm mai întâi o privire asupra funcțiilor care sunt comune atât în NumPy, cât și în SciPy.

Interacțiunea cu NumPy:

SciPy se bazează pe NumPy și, prin urmare, puteți utiliza funcțiile NumPy în sine pentru a manipula array-uri. Pentru a cunoaște în profunzime aceste funcții, puteți utiliza pur și simplu funcțiile help(), info() sau source().

help():

Pentru a obține informații despre orice funcție, puteți utiliza funcția help(). Există două moduri în care poate fi utilizată această funcție:

• fără parametri
• cu ajutorul parametrilor

Iată un exemplu care prezintă ambele metode de mai sus:

from scipy import cluster 
help(cluster) #with parameter 
help() #without parameter

Când executați codul de mai sus, primul help() returnează informații despre submodulele cluster. A doua help() cere utilizatorului să introducă numele oricărui modul, cuvânt cheie, etc. pentru care dorește să caute informații. Pentru a opri execuția acestei funcții, este suficient să tastați ‘quit’ și să apăsați enter.

info():

Această funcție returnează informații despre funcțiile, modulele, etc. dorite.

scipy.info(cluster)

source():

Codul sursă este returnat numai pentru obiectele scrise în Python. Această funcție nu returnează informații utile în cazul în care metodele sau obiectele sunt scrise în orice alt limbaj, cum ar fi C. Cu toate acestea, în cazul în care doriți să folosiți această funcție, o puteți face după cum urmează:

scipy.source(cluster)

Funcții speciale:

SciPy oferă o serie de funcții speciale care sunt utilizate în fizica matematică, cum ar fi eliptica, funcții de conveniență, gamma, beta, etc. Pentru a căuta toate funcțiile, puteți utiliza funcția help() așa cum a fost descrisă anterior.

Funcții exponențiale și trigonometrice:

Pachetul Special Function al lui SciPy oferă un număr de funcții prin care puteți găsi exponenți și rezolva probleme trigonometrice.

Considerați următorul exemplu:

EXEMPLU:

from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)

IEȘIRE:

1000.0
8.0
1.0
0.7071061067811865475

Există multe alte funcții prezente în pachetul de funcții speciale din SciPy pe care le puteți încerca singuri.

Funcții de integrare:

SciPy oferă o serie de funcții pentru rezolvarea integralelor. De la integratorul diferențial obișnuit până la utilizarea regulilor trapezoidale pentru a calcula integralele, SciPy este un depozit de funcții pentru a rezolva toate tipurile de probleme de integrale.

Integrare generală:

SiPy oferă o funcție numită quad pentru a calcula integrala unei funcții care are o singură variabilă. Limitele pot fi ( ) pentru a indica limitele infinite. Sintaxa funcției quad() este următoarea:

SYNTAX:

quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)

Aici, funcția va fi integrată între limitele a și b (poate fi și infinită).

EXEMPLU:

from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)

În exemplul de mai sus, funcția ‘a’ este evaluată între limitele 0, 1. Când acest cod este executat, veți vedea următoarea ieșire.

EXIT:

(3.9086503371292665, 4.3394735994897923e-14)

Funcție integrală dublă:

SciPy oferă dblquad care poate fi folosit pentru a calcula integralele duble. O integrală dublă, după cum mulți dintre noi știu, constă din două variabile reale. Funcția dblquad() va lua ca parametru funcția care urmează să fie integrată, împreună cu alte 4 variabile care definesc limitele și funcțiile dy și dx.

EXEMPLU:

from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)

SURSA:

-1.3333333333333333333335, 1.4802973661668755e-14)

SciPy oferă diverse alte funcții de evaluare a integralelor triple, a integralelor n, a integralelor Romberg, etc. pe care le puteți explora mai în detaliu. Pentru a găsi toate detaliile despre funcțiile necesare, utilizați funcția de ajutor.

Funcții de optimizare:

Scipy.optimize oferă o serie de algoritmi de optimizare utilizați în mod obișnuit, care pot fi văzuți utilizând funcția de ajutor.

Este format în principiu din următoarele:

• Minimizarea neconstrânsă și constrânsă a funcțiilor scalare multivariate, adică minimizarea (de exemplu BFGS, Newton Conjugate Gradient, Nelder_mead simplex, etc)
• Rutine de optimizare globală (de exemplu. differential_evolution, dual_annealing, etc)
• Minimizarea celor mai mici pătrate și ajustarea curbelor (ex. least_squares, curve_fit, etc)
• Minimizatoare de funcții scalare univariate și găsitori de rădăcini (ex. minimize_scalar și root_scalar)
• Soluționatoare de sisteme de ecuații multivariate care utilizează algoritmi precum Powell hibrid, Levenberg-Marquardt.

Funcția Rosenbrook:

Funcția Rosenbrook ( rosen) este o problemă de testare utilizată pentru algoritmii de optimizare pe bază de gradient. Este definită după cum urmează în SciPy:

EXEMPLU:

import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)

SURSA: 7371.03999999999999999945

Nelder-Mead:

Metoda Nelder-Mead este o metodă numerică utilizată adesea pentru a găsi min/max a unei funcții într-un spațiu multidimensional. În exemplul următor, metoda de minimizare este utilizată împreună cu algoritmul Nelder-Mead.

EXEMPLU:

from scipy import optimize
a = 
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x

OUTPUT: array()

Funcții de interpolare:

În domeniul analizei numerice, interpolarea se referă la construirea de noi puncte de date în cadrul unui set de puncte de date cunoscute. Biblioteca SciPy constă într-un subpachet numit scipy.interpolate care cuprinde funcții și clase de spline, clase de interpolare unidimensională și multidimensională (univariată și multivariată) etc.

Interpolare univariată:

Interpolarea univariată este, în principiu, un domeniu de ajustare a curbelor care găsește curba care oferă o potrivire exactă la o serie de puncte de date bidimensionale. SciPy oferă funcția interp1d care poate fi utilizată pentru a produce interpolarea univariată.

EXEMPLU:

import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()

OUTPUT:

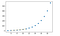
Interpolare multivariată:

Interpolarea multivariată (interpolare spațială ) este un tip de interpolare pe funcții care constau din mai multe variabile. Exemplul următor demonstrează un exemplu de
Interpolare pe o grilă bidimensională folosind funcția interp2d(x, y, z) Practic, va folosi array-urile x, y, z pentru a aproxima o anumită funcție interp2d. f: „z = f(x, y)” și returnează o funcție a cărei metodă de apelare folosește interpolarea spline pentru a găsi valoarea noilor puncte.
EXEMPLU:

from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()

IEȘIRE:

Funcții transformate Fourier:

Analiza Fourier este o metodă care se ocupă cu exprimarea unei funcții ca o sumă de componente periodice și recuperarea semnalului din aceste componente. Funcțiile fft pot fi utilizate pentru a returna transformata Fourier discretă a unei secvențe reale sau complexe.

EXEMPLU:

from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)

SURSA:

În mod similar, puteți găsi inversul acesteia folosind funcția ifft, după cum urmează:

EXEMPLU:

rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)

OUTPUT:

Funcții de prelucrare a semnalelor:

Prelucrarea semnalelor se ocupă cu analiza, modificarea și sintetizarea semnalelor, cum ar fi sunetul, imaginile etc. SciPy oferă câteva funcții cu ajutorul cărora puteți proiecta, filtra și interpola date unidimensionale și bidimensionale.

Filtrare:

Prin filtrarea unui semnal, practic eliminați componentele nedorite din acesta. Pentru a efectua o filtrare ordonată, puteți utiliza funcția order_filter. Practic, această funcție efectuează o filtrare ordonată pe o matrice. Sintaxa acestei funcții este următoarea:

SYNTAX:

order_filter(a, domain, rank)

a = tablou de intrare cu N dimensiuni

domain = tablou mască având același număr de dimensiuni ca `a`

rank = număr negativ care selectează elementele din listă după ce aceasta a fost ordonată (0 este cel mai mic urmat de 1…)

EXEMPLU:

from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))

OUTPUT:

]

]

Waveforms:

The scipy.signal subpachet constă, de asemenea, în diverse funcții care pot fi utilizate pentru a genera forme de undă. Una dintre aceste funcții este chirp. Această funcție este un generator de cosinus cu baleiaj de frecvență, iar sintaxa este următoarea:

SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)

where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()

OUTPUT:

Algebră liniară:

Algebra liniară se ocupă cu ecuațiile liniare și reprezentările lor folosind spații vectoriale și matrici. SciPy este construit pe bibliotecile ATLAS LAPACK și BLAS și este extrem de rapid în rezolvarea problemelor legate de algebra liniară. În plus față de toate funcțiile din numpy.linalg, scipy.linalg oferă, de asemenea, o serie de alte funcții avansate. De asemenea, dacă numpy.linalg nu este utilizat împreună cu suportul ATLAS LAPACK și BLAS, scipy.linalg este mai rapid decât numpy.linalg.

Căutarea inversului unei matrici:

Matematic, inversul unei matrice A este matricea astfel încât unde este matricea identitate formată din unu pe diagonala principală notată ca B=A-1. În SciPy, această inversă poate fi obținută cu ajutorul metodei linalg.inv.

EXEMPLU:

import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)

OUTPUT:

]

Căutarea determinanților:

Valoarea derivată aritmetic din coeficienții matricei este cunoscută sub numele de determinantul unei matrice pătrate. În SciPy, acest lucru se poate face folosind o funcție det care are următoarea sintaxă:

SYNTAX:
det(a, overwrite_a=False, check_finite=True)
unde,

a : (M, M) Este o matrice pătrată

overwrite_a( bool, opțional) : Permite suprascrierea datelor din a

check_finite ( bool, opțional): Pentru a verifica dacă matricea de intrare este formată numai din numere finite

EXEMPLU:

import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)

IEȘIRE: -5.0

Valori proprii disparate:

Valorile proprii sunt un set specific de scalari legați de ecuații liniare. ARPACK oferă care vă permit să găsiți valorile proprii ( vectori proprii ) destul de rapid. Întreaga funcționalitate a ARPACK este împachetată în două interfețe de nivel înalt care sunt scipy.sparse.linalg.eigs și scipy.sparse.linalg.eigsh. eigs. Interfața eigs vă permite să găsiți valorile proprii ale matricilor pătrate nesimetrice reale sau complexe, în timp ce interfața eigsh conține interfețe pentru matrici reale-simetrice sau complexe-hermitiene.

Funcția eigh rezolvă o problemă generalizată de valori proprii pentru o matrice hermitiană complexă sau reală simetrică.

EXEMPLU:

from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)

IEȘIRE:

Valori proprii selectate :
Complex ndarray :

]

Spatial Data Structures and Algorithms:

Datele spațiale constau, în principiu, din obiecte care sunt formate din linii, puncte, suprafețe etc. Pachetul scipy.spatial din SciPy poate calcula diagrame Voronoi, triangulații etc. folosind biblioteca Qhull. De asemenea, constă în implementări KDTree pentru interogări ale punctului cel mai apropiat de cel mai apropiat vecin.

Tangulații Delaunay:

Matematic, triangulațiile Delaunay pentru un set de puncte discrete într-un plan este o triangulație astfel încât niciun punct din setul dat de puncte să nu se afle în interiorul circumferinței oricărui triunghi.

EXEMPLU:

import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()

IEȘIRE:

Funcții de prelucrare a imaginilor multidimensionale:

Prelucrarea imaginilor se ocupă, în esență, cu efectuarea de operații asupra unei imagini pentru a prelua informații sau pentru a obține o imagine îmbunătățită din cea originală. Pachetul scipy.ndimage constă într-un număr de funcții de procesare și analiză a imaginilor concepute pentru a lucra cu matrici de dimensionalitate arbitrară.

Convoluție și corelație:

SciPy oferă un număr de funcții care permit corelarea și convoluția imaginilor.

• Funcția correlate1d poate fi utilizată pentru a calcula corelația unidimensională de-a lungul unei axe date
• Funcția correlate permite corelația multidimensională a oricărei matrice date cu nucleul specificat
• Funcția convolve1d poate fi utilizată pentru a calcula corelația unidimensională cu un nucleu specificat
• .convoluție multidimensională de-a lungul unei axe date

Funcția convolve permite convoluția multidimensională a oricărei matrice date cu nucleul specificat

EXEMPLU:

import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)

OUTPUT: array()

File IO:

Filele scipy.io oferă o serie de funcții care vă ajută să gestionați fișiere de diferite formate, cum ar fi fișiere MATLAB, fișiere IDL, fișiere Matrix Market, etc.

Pentru a utiliza acest pachet, va trebui să-l importați după cum urmează:

import scipy.io as sio

Pentru informații complete despre subpachet, puteți consulta documentul oficial despre File IO.

Aceasta ne aduce la sfârșitul acestui tutorial SciPy. Sper că ați înțeles totul în mod clar. Asigurați-vă că practicați cât mai mult posibil.

Dacă doriți să consultați mai multe articole despre tehnologiile cele mai în vogă de pe piață, cum ar fi Inteligența Artificială, DevOps, Ethical Hacking, atunci puteți consulta site-ul oficial Edureka.

Să urmăriți și alte articole din această serie care vor explica diverse alte aspecte ale Python și Știința Datelor.

1. Machine Learning Classifier in Python

2. Python Scikit-Learn Cheat Sheet

3. Machine Learning Tools

4. Python Libraries For Data Science And Machine Learning

5. Python Libraries For Data Science And Machine Learning

6. Chatbot în Python

6. Colecții Python

7. Module Python

8. Competențe pentru dezvoltatorii Python

9. Întrebări și răspunsuri la interviuri OOPs

10. Curriculum vitae pentru un dezvoltator Python

11. Analiza exploratorie a datelor în Python

12. Joc cu șerpi cu modulul Turtle din Python

13. Salariul dezvoltatorului Python

14. Analiza componentelor principale

15. Python vs C++

16. Tutorial Scrapy

17. Web Scraping cu Python

18. Metoda de regresie a celor mai mici pătrate

19. Jupyter Notebook Cheat Sheet

20. Bazele Python

21. Programe model Python

22. Generatoare în Python

23. Decorator în Python

24. Python Spyder IDE

25. Aplicații mobile folosind Kivy în Python

26. Top 10 cele mai bune cărți pentru a învăța & practică Python

27. Cadru pentru roboți cu Python

28. Joc cu șerpi în Python folosind PyGame

29. Întrebări și răspunsuri la interviul Django

30. Top 10 aplicații Python

31. Tabele Hash și Hashmaps în Python

32. Python 3.8

33. Mașina vectorială de suport

34. Tutorial Python

.