![]()
„Oamenii vorbesc despre uciderea timpului, în timp ce timpul îi ucide în liniște”
Dion Boucicault – London Assurance (1841)
- Până în prezent am considerat cinematica și dinamica particulelor, inclusiv mișcarea de translație și circulară, precum și mișcarea de translație a sistemelor de particule (în special a corpurilor rigide) în termeni de mișcare a centrului de masă al sistemului (corpului). În acest din urmă caz ne putem imagina că toată masa obiectului este localizată în centrul de masă în ceea ce privește forțele de translație externe.
-
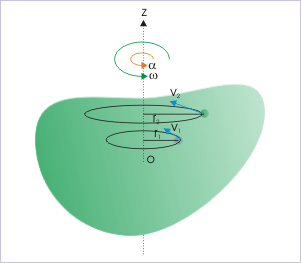 Postul următor este de a considera rotația unui corp rigid în jurul unei axe fixe de rotație. Rețineți că, deoarece avem în vedere un corp rigid, fiecare particulă din corp rămâne fixă în raport cu celelalte. Aceasta înseamnă că, într-o astfel de mișcare de rotație, fiecare particulă se deplasează într-un cerc al cărui centru se află pe axa de rotație. În diagrama din dreapta, obiectul se rotește în jurul axei z; cele două particule de probă se deplasează în cercuri cu razele r1 și r2. Dacă putem descrie mișcarea circulară a unei particule, fără a face referire directă la raza acesteia, atunci toate particulele din sistem vor fi descrise de același set de ecuații. Deși razele particulelor sunt diferite, rotațiile lor unghiulare sunt identice. Prin urmare, este necesar să se introducă variabile unghiulare.
Postul următor este de a considera rotația unui corp rigid în jurul unei axe fixe de rotație. Rețineți că, deoarece avem în vedere un corp rigid, fiecare particulă din corp rămâne fixă în raport cu celelalte. Aceasta înseamnă că, într-o astfel de mișcare de rotație, fiecare particulă se deplasează într-un cerc al cărui centru se află pe axa de rotație. În diagrama din dreapta, obiectul se rotește în jurul axei z; cele două particule de probă se deplasează în cercuri cu razele r1 și r2. Dacă putem descrie mișcarea circulară a unei particule, fără a face referire directă la raza acesteia, atunci toate particulele din sistem vor fi descrise de același set de ecuații. Deși razele particulelor sunt diferite, rotațiile lor unghiulare sunt identice. Prin urmare, este necesar să se introducă variabile unghiulare.
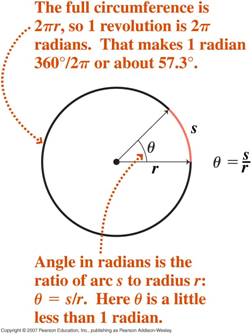
- Măsura în radiani a unghiurilor
- Viteza (viteza) unghiulară și accelerația unghiulară
Viteza unghiulară și accelerația unghiulară sunt definite într-un mod similar cu viteza și accelerația. Există valori medii și instantanee pentru fiecare dintre ele.
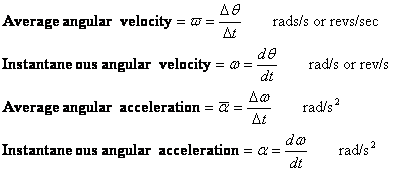
![]() Accelerația unghiulară nu este același lucru cu accelerația centripetă. Accelerația centripetă se datorează unei modificări a direcției vitezei, accelerația unghiulară se datorează unei modificări a mărimii vitezei (prin unghiul de rotație).
Accelerația unghiulară nu este același lucru cu accelerația centripetă. Accelerația centripetă se datorează unei modificări a direcției vitezei, accelerația unghiulară se datorează unei modificări a mărimii vitezei (prin unghiul de rotație).
![]() Exact ca în cazul translației, diferența dintre viteza unghiulară și viteza unghiulară este direcția. Viteza unghiulară trebuie să includă o direcție de rotație în jurul axei în cauză. De exemplu, 10 rad/s în sensul acelor de ceasornic în jurul axei x este o viteză unghiulară, 10 rad/s în jurul axei x este o viteză unghiulară.
Exact ca în cazul translației, diferența dintre viteza unghiulară și viteza unghiulară este direcția. Viteza unghiulară trebuie să includă o direcție de rotație în jurul axei în cauză. De exemplu, 10 rad/s în sensul acelor de ceasornic în jurul axei x este o viteză unghiulară, 10 rad/s în jurul axei x este o viteză unghiulară.
- Ecuații cinematice de rotație
Prin analogie directă cu ecuațiile cinematice de translație, mișcarea circulară în jurul unei singure axe sub accelerație unghiulară constantă poate fi descrisă prin următoarele patru ecuații,
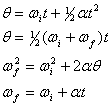
unde am făcut înlocuirile, ![]()
Rețineți că, la fel cum +x este definit în mod arbitrar la dreapta, valoarea pozitivă a lui theta poate fi definită ca fiind în sensul acelor de ceasornic sau în sens invers.
- Relația dintre variabilele unghiulare și de translație
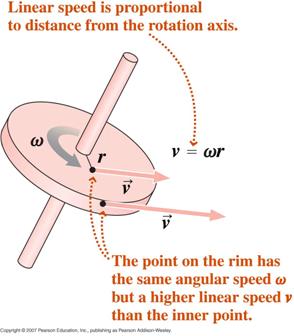 Plecând de la definiția măsurii radianului, prin diferențiere în raport cu timpul, putem arăta că,
Plecând de la definiția măsurii radianului, prin diferențiere în raport cu timpul, putem arăta că,
![]()
unde v este viteza tangențială și a este accelerația tangențială.
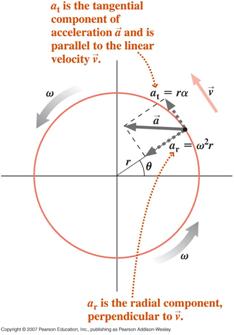
![]() O particulă care execută o mișcare circulară, cu o viteză unghiulară variabilă (mișcare circulară neuniformă), va experimenta două componente ale accelerației, o componentă tangențială datorată mărimii variabile a vitezei sale și o componentă radială (centripetă) datorată schimbării direcției vitezei sale
O particulă care execută o mișcare circulară, cu o viteză unghiulară variabilă (mișcare circulară neuniformă), va experimenta două componente ale accelerației, o componentă tangențială datorată mărimii variabile a vitezei sale și o componentă radială (centripetă) datorată schimbării direcției vitezei sale
![]()
Accelerația netă a particulei este suma vectorială a acestor două componente, așa cum este indicat mai jos.
- Pentru informarea dumneavoastră…
Rotația simultană în jurul mai multor axe poate fi considerată într-un mod similar cu mișcarea proiectilului, unde am extins discuția noastră despre translația 1D la mișcarea 2D. În aplicațiile aeronautice, rotațiile în jurul celor trei axe sunt descrise ca Roll, Pitch și Yaw.
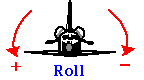
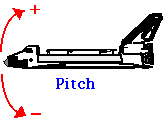
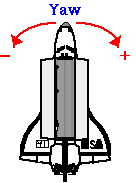

.
Exemplu de problemă
![]()
„Nu vreau să ating nemurirea prin munca mea…Vreau să o obțin prin faptul că nu mor”
Woody Allen – Woody Allen și comedia sa (1975)
![]()
Dr. C. L. Davis
Departamentul de Fizică
Universitatea din Louisville
email: [email protected]

.