Cum să gândești cu exponenți și logaritmi

Iată un truc pentru a gândi la problemele care implică exponenți și logaritmi. Puneți doar două întrebări:

1) Vorbim despre intrări (cauza schimbării) sau ieșiri (schimbarea reală care s-a produs?)

Logaritmii dezvăluie intrările care au cauzat creșterea
Exponenții găsesc rezultatul final al creșterii

2) Vorbim despre perspectiva cultivatorului sau a unui observator?

e și logaritmul natural sunt din perspectiva instantanee a cultivatorului
Baza 10, baza 2, etc. sunt măsurători convenabile pentru un observator uman

În capul meu, pun opțiunile într-un tabel:

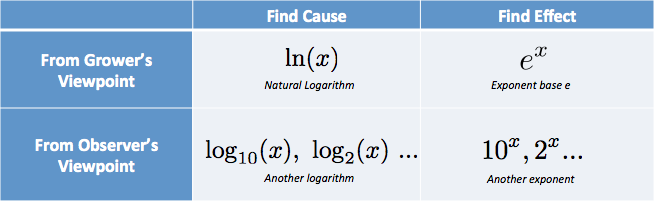
exponent logaritm punct de vedere comparat

Am gânduri de genul „am nevoie de cauză, din perspectiva cultivatorului… care este log natural.”. (Natural log este prescurtat cu minusculă LN, de la high-falutin’ logarithmus naturalis.)

Am fost frustrat de cursurile care descriau partea interioară a tabelului, funcțiile brute, fără legendele care explicau când să le folosim!”

Nu merge așa, hai să facem practică directă de gândire cu logaritmi și exponenți.

Scenariu: Descrierea creșterii PIB-ului

Iată un exemplu tipic de creștere:

Din 2000 până în 2010, PIB-ul SUA s-a schimbat de la 9,9 trilioane la 14,4 trilioane

Ok, sigur, aceste numere arată că a avut loc o schimbare. Dar, probabil, dorim o înțelegere a cauzei: Ce rată medie anuală de creștere ar putea explica această schimbare?

Imediat, creierul meu se gândește la „logaritmi”, deoarece lucrăm în sens invers, de la creștere la rata care a cauzat-o. Încep cu un gând de genul acesta:

$\displaystyle{\text{logaritmul de schimbare} \rightarrow \text{causa creșterii} }$

Un început bun, dar haideți să îl ascuțim.

În primul rând, ce logaritm ar trebui să folosim?

În mod implicit, aleg logaritmul natural. Cele mai multe evenimente sfârșesc prin a fi în termeni de cultivator (nu de observator), iar mie îmi place să „călătoresc împreună” cu elementul în creștere pentru a vizualiza ce se întâmplă. (Radianții sunt similari: ei măsoară unghiurile în termenii celui care mișcă.)

Întrebarea următoare: la ce schimbare aplicăm logaritmul?

De fapt, ne interesează doar raportul dintre început și sfârșit: de la 9,9 trilioane la 14,4 trilioane în 10 ani. Aceasta este aceeași rată de creștere ca și cum am trece de la 9,90$ la 14,40$ în aceeași perioadă.

Ne putem ascuți gândul:

$\displaystyle{\text{ logaritmul natural al raportului de creștere} \rightarrow \text{causa creșterii} }$

$\displaystyle{\ln(\frac{14,4}{9,9}) = 0,374}$

Ok, cauza a fost o rată de 0,374 sau 37,4%. Am terminat?

Nu încă. Logaritmii nu știu despre cât timp a durat o schimbare (nu am băgat 10 ani, nu?). Ei ne dau o rată ca și cum toată schimbarea s-ar fi petrecut într-o singură perioadă de timp.

Schimbarea ar putea fi, într-adevăr, un singur an de creștere continuă de 37,4%, sau 2 ani de creștere de 18,7%, sau o altă combinație.

Din scenariu, știm că schimbarea a durat 10 ani, așa că rata trebuie să fi fost:

$\displaystyle{ \text{rata} = \frac{.374}{10} = 0,0374 = 3,74\%}$

Din punctul de vedere al creșterii instantanee, continue, economia SUA a crescut cu 3,74% pe an.

Am terminat acum? Nu chiar!

Această rată continuă este din punctul de vedere al creșterii, ca și cum am „merge împreună” cu economia pe măsură ce aceasta se schimbă. Unui bancher probabil îi pasă de diferența de la an la an, prietenoasă pentru oameni. Ne putem da seama de acest lucru lăsând creșterea continuă să ruleze timp de un an:

$\displaystyle{\text{exponent cu rată și timp} \rightarrow \text{efectul creșterii} }$

$\displaystyle{e^{\text{rate} \cdot \text{time}} = \text{growth}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

Câștigul de la un an la altul este de 3,8%, ușor mai mare decât rata instantanee de 3,74% datorată capitalizării. Iată un alt mod de a prezenta situația:

Din punct de vedere instantaneu, o anumită parte a economiei crește cu 3,74%, modelată de $e^(.0374 * ani)$
De la an la an, calculând efectele compuse, economia crește cu 3,81%, modelată prin $1,0381^ani$

În finanțe, este posibil să dorim variația de la un an la altul, care poate fi comparată frumos cu alte tendințe. În știință și inginerie, preferăm modelarea comportamentului pe bază instantanee.

Scenariu: Descrierea creșterii naturale

Detestesc exemplele artificialiste de genul „Presupunând că o bacterie se dublează la fiecare 24 de ore, găsiți formula sa de creștere.”. Se replică coloniile de bacterii la intervale umane curate și așteptăm o dublare exactă?

Un scenariu mai bun: „Hei, am găsit niște bacterii, am așteptat o oră, iar grumazul a crescut de la 2,3 grame la 2,32 grame. Mă duc să iau prânzul acum. Calculați cât de mult vom avea când mă întorc peste 3 ore.”

Să modelăm acest lucru. Vom avea nevoie de un logaritm pentru a găsi rata de creștere și apoi de un exponent pentru a proiecta această creștere în viitor. Ca și înainte, să păstrăm totul în termenii logaritmului natural pentru început.

Factorul de creștere este:

$\displaystyle{\text{logaritmul de schimbare} \rightarrow \text{caz de creștere} }$

$\displaystyle{\ln(\text{crestere}) = \ln(2.32/2.3) = 0.0086 = 0.86\%}$

Aceasta este rata pentru o oră, iar modelul general pentru a proiecta în viitor va fi

$\displaystyle{\text{exponent cu rata și timpul} \rightarrow \text{efectul creșterii} }$

$\displaystyle{e^{.0086 \cdot \text{oră}}. \rightarrow \text{efectul creșterii} }$

Dacă începem cu 2.32 și creștem timp de 3 ore vom avea:

$\displaystyle{2.32 \cdot e^{.0086 \cdot 3} = 2.38}$

Doar ca să ne distrăm, cât durează până când bacteria se dublează? Imaginați-vă că așteptați ca 1 să se transforme în 2:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{ore}} = 2}$

Potem lua mecanic log natural al ambelor părți pentru a „anula exponentul”, dar haideți să gândim intuitiv.

Dacă 2 este rezultatul final, atunci ln(2) este aportul de creștere care ne-a dus acolo (o anumită rată × timp). Știm că rata a fost de 0,0086, deci timpul pentru a ajunge la 2 ar fi:

$\displaystyle{ \text{ore} = \frac{\ln(2)}{\text{rata}} = \frac{.693}{.0086} = 80.58}$

Colonia se va dubla după ~80 de ore. (Te bucuri că nu ai rămas pe aici?)

Ce înseamnă cu adevărat schimbarea de perspectivă?

Descoperirea faptului dacă doriți input (cauza creșterii) sau output (rezultatul creșterii) este destul de simplă. Dar cum vizualizați perspectiva cultivatorului?

Imaginați-vă că avem mici lucrători care construiesc modelul final de creștere (vezi articolul despre exponenți):

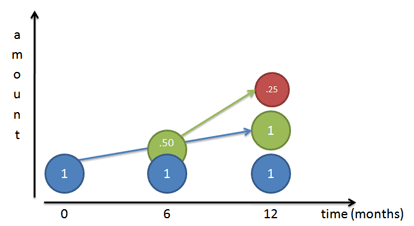
$interesul compus$

Dacă rata noastră de creștere este de 100%, îi spunem lucrătorului nostru inițial (domnul Albastru) să muncească în mod constant și să creeze o copie 100% din el însuși până la sfârșitul anului. Dacă îl urmărim zi de zi, vedem că el termină într-adevăr o copie 100% din el însuși (domnul Green) la sfârșitul anului.

Dar… acel lucrător pe care îl construia (domnul Green) începe să lucreze și el. Dacă domnul Green apare pentru prima dată la 6 luni, el are la dispoziție o jumătate de an pentru a lucra (același ritm anual ca și domnul Blue) și îl construiește pe domnul Red. Bineînțeles, dl Roșu ajunge să fie pe jumătate terminat, deoarece dl Verde are la dispoziție doar 6 luni.

Ce s-ar întâmpla dacă dl Verde ar apărea după 4 luni? O lună? O zi? O secundă? Dacă lucrătorii încep să crească imediat, obținem curba instantaneu-cu-instant definită de $e^x$:

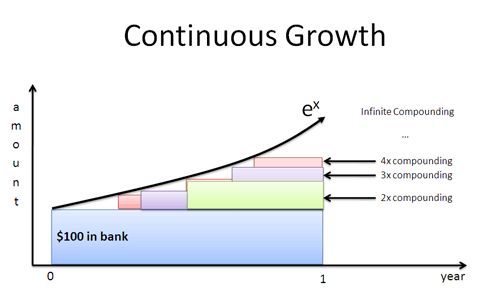
creștere continuă

Loganul natural oferă o rată de creștere în termenii perspectivei unui lucrător individual. Introducem această rată în $e^x$ pentru a găsi rezultatul final, cu toate compunerile incluse.

Utilizarea altor baze

Căutarea unui alt tip de logaritm (baza 10, baza 2 etc.) înseamnă că suntem în căutarea unui anumit tipar în creșterea globală, nu a ceea ce face lucrătorul individual.

Care logaritm pune o întrebare atunci când vede o schimbare:

Baza logaritmică e: Care a fost ritmul instantaneu urmat de fiecare muncitor?
Bază logaritmică 2: Câte dublări au fost necesare?
Bază logaritmică 10: Câte dublări de 10 ori au fost necesare?

Iată un scenariu de analizat:

În decurs de 30 de ani, numărul de tranzistori de pe cipurile tipice a trecut de la 1000 la 1 miliard

Cum ați analiza acest lucru?

Microcipurile nu sunt o entitate unică care crește lin în timp. Sunt ediții separate, de la companii concurente, și indică o tendință tehnologică generală.
Din moment ce nu „mergem împreună” cu un microcip în expansiune, să folosim un cântar făcut pentru comoditatea umană. Este mai ușor să ne gândim la dublare decât la 10x.

Cu aceste ipoteze obținem:

$\displaystyle{\text{logaritmul de schimbare} \rightarrow \text{caz de creștere} }$

$\displaystyle{\log_2(\frac{\text{1 miliard}}{1000}) = \log_2(\text{1 milion}) \sim \text{20 de dublări}}$

„Cauza creșterii” a fost 20 de dublări, despre care știm că au avut loc pe parcursul a 30 de ani. Aceasta reprezintă o medie de 2/3 dublări pe an, sau 1,5 ani pentru fiecare dublare – o regulă de bază frumoasă.

Din perspectiva cultivatorului, am calcula $\ln(\text{1 miliard}/1000) / \text{30 ani} = 46\%$ creștere continuă (un pic mai greu de raportat în acest scenariu).

Potem rezuma analiza noastră într-un tabel:

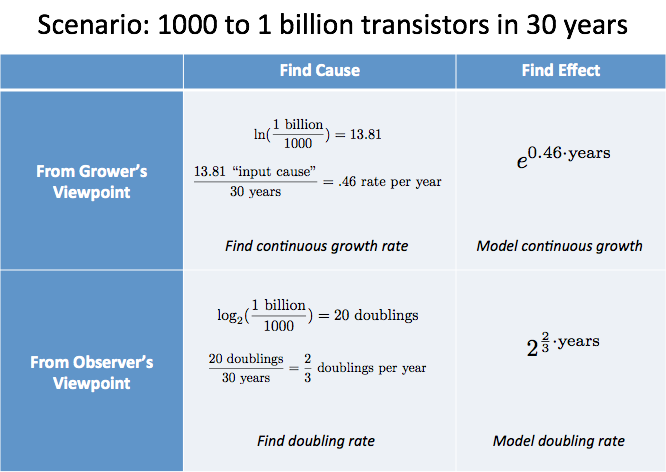
exponenți tranzistor exemplu

Rezumat

Învățarea constă în a găsi legendele ascunse în spatele unui concept. Când se folosește? Ce punct de vedere aduce la problemă?

Interpretarea mea actuală este că exponenții întreabă despre cauză vs. efect și cultivator vs. observator. Dar nu am terminat niciodată; o parte din distracție este să vedem cum putem recapitula concepte vechi.

Matematică fericită.

Apendice: Formula schimbării bazei

Iată cum să ne gândim la schimbarea bazei. Presupunând o rată de creștere continuă de 100%,

ln(x) este timpul pentru a crește până la x
ln(2) este timpul pentru a crește până la 2

Din moment ce avem timpul de dublare, putem vedea câte ar „încăpea” în timpul total pentru a crește până la x:

$\displaystyle{\text{numărul dublărilor de la 1 la x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

De exemplu, câte dublări au loc de la 1 la 64?

Păi, ln(64) = 4,158. Iar ln(2) = 0,693. Numărul de dublări care se potrivesc este:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4.158}{.693} = 6}$

În lumea reală, calculatoarele pot pierde precizie, așa că folosiți o funcție logaritmică directă în baza 2 dacă este posibil. Și, bineînțeles, putem avea un număr fracționar: Trecerea de la 1 la rădăcina pătrată a lui 2 este o „jumătate” de dublare, sau log2(1,414) = 0,5.

Schimbarea la log baza 10 înseamnă că numărăm numărul de 10x-uri care se potrivesc:

$\displaystyle{\text{numărul de 10x-uri de la 1 la x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Frumos, nu? Citiți Using Logarithms in the Real World (Utilizarea logaritmilor în lumea reală) pentru mai multe exemple.

Alte postări din această serie

Un ghid intuitiv al funcțiilor exponențiale & e
Demistificarea logaritmului natural (ln)
Un ghid vizual al ratelor dobânzii simple, compuse și continue
Definiții comune ale lui e (colorate)
Înțelegerea exponenților (De ce 0^0 = 1?)
Utilizarea logaritmilor în lumea reală
Cum să gândești cu exponenți și logaritmi
Înțelegerea creșterii discrete vs. continue
Ce înseamnă cu adevărat un exponent?
Întrebare: De ce este e special? (2,718…., nu 2, 3,7 sau un alt număr?)