
Rețelele neuronale și matematica sunt inseparabile și probabil că asta îi sperie pe cei mai mulți oameni. Am auzit prea multe remarci dubioase despre Deep Learning: „Oh, este prea multă matematică pentru mine ca să o înțeleg”, „Câte companii folosesc cu adevărat Deep Learning? Aș prefera să mă scutesc de frământări de creier și să stau departe de aceste concepte solicitante”.
Dar dacă te gândești bine, nu este atât de dificil. Aveți încredere în mine! Pentru a înțelege de ce un algoritm se comportă într-un anumit fel, este esențial să înțelegem ce se întâmplă în spatele scenei. Algoritmii complecși de învățare automată sunt împachetați convenabil pentru noi astăzi și sunt doar la un apel de funcție distanță. Derivatele funcțiilor de activare sunt concepte ceva mai puțin evidente pe care avem adesea tendința de a le ignora. Cu toate acestea, ele stau la baza unor algoritmi puternici și depunerea unui mic efort suplimentar pentru a le înțelege dă cu siguranță roade. După ce veți citi acest articol veți fi cu un pas mai aproape de a desluși ce se află sub fațada „cutiei negre”.
Background
Rețelele neuronale utilizează o varietate de funcții de activare în straturile ascunse și de ieșire pentru a cataliza procesul de învățare. Câteva funcții de activare utilizate în mod obișnuit includ funcțiile Sigmoid și tanH. Cea mai populară funcție de activare este ReLU („Rectified Linear Unit”) datorită capacității sale de a depăși în mod eficient problema gradientului de dispariție. O înțelegere în profunzime a funcțiilor de activare este pentru o altă zi. Astăzi ne vom concentra pe matematica din spatele derivatei funcției Sigmoid.
De ce este importantă derivata unei funcții de activare?
După cum probabil știți, două etape conduc rețelele neuronale:
- Propagare directă – Datele de intrare trec prin rețea și obținem ieșirea prezisă. O comparăm cu ieșirea reală și calculăm eroarea.
- Propagare inversă – Eroarea calculată este folosită pentru a actualiza parametrii rețelei neuronale folosind derivata funcției de activare.
Funcția sigmoidă
Funcția sigmoidă, caracterizată de o curbă în formă de S, este adesea menționată ca un caz special al funcției logistice. Ea este cea mai utilă în cazurile în care trebuie să prezicem probabilitatea ca ieșire.
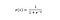
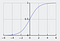
Funcția sigmoidă produce valori care se situează între 0 și 1 (pe bună dreptate, având în vedere că prezice probabilități).
Derivata sigmoidală
Această componentă fundamentală care ajută la antrenarea rețelelor neuronale ia forma:


Sfârșit, să ne apucăm de derivare!
Apariția 1

Apariția 2:
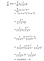
De ce folosim această versiune a derivatului?
În etapa de propagare înainte, calculați funcția sigmoidă (σ(x)) și aveți la îndemână valoarea acesteia. În timp ce calculați derivata în etapa de propagare inversă, tot ce trebuie să faceți este să introduceți valoarea lui σ(x) în formula derivată mai sus și iată, sunteți gata de plecare!
Asta e tot, băieți! Vă mulțumim că ați citit!