Formule Pi

Posted on by admin
Teoria numerelor > Constante > Pi >
Calcul și analiză > Serii > Formule BBP >
Calcul și analiză > Calcul > Calcul >. Integrale > Integrale definite >
MathWorld Contributors > Cloitre >
MathWorld Contributors > Plouffe >
MathWorld Contributors > Sondow >

Less…

DOWNLOAD Mathematica Notebook

Există multe formule de pi de mai multe tipuri. Printre altele, acestea includ serii, produse, construcții geometrice, limite, valori speciale și iterații pi.

pi este intim legat de proprietățile cercurilor și sferelor. Pentru un cerc de rază r, circumferința și aria sunt date de

C = 2pir
(1)
A = pir^2.
(2)

În mod similar, pentru o sferă de rază r, suprafața și volumul închis sunt

.

S = 4pir^2
(3)
V = 4/3pir^3.
(4)

O formulă exactă pentru pi în termeni de tangente inverse ale fracțiilor unitare este formula lui Machin

1/4pi=4tan^(-1)(1/5)-tan^(-1)(1/(239)).
(5)

Există alte trei formule asemănătoare cu cea a lui Machin,precum și mii de alte formule similare care au mai mulți termeni.

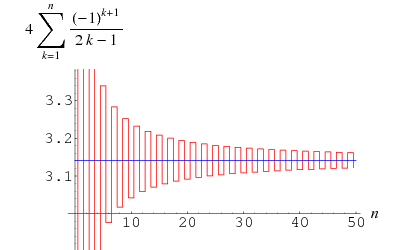
GregorySeries

Gregory și Leibniz au găsit

pi/4 = suma_(k=1)^(infty)((-1)^(k+1))/(2k-1)
(6)
= 1-1/3+1/5-....
(7)

(Wells 1986, p. 50), care este cunoscută sub numele de seria Gregory și poate fi obținută prin introducerea lui x=1 în seria Leibniz pentru tan^(-1)x. Eroarea după cel de-al nlea termen al acestei serii din seria Gregory este mai mare decât (2n)^(-1), astfel încât această sumă converge atât de lent încât 300 de termeni nu sunt suficienți pentru a calcula corect pi cu două zecimale! Totuși, ea poate fi transformată în

pi=suma_(k=1)^infty(3^k-1)/(4^k)zeta(k+1),
(8)

unde zeta(z) este funcția zeta Riemann (Vardi 1991, pp. 157-158; Flajolet și Vardi 1996), astfel încât eroarea după k termeni este aproximativ (3/4)^k.

O serie de sume infinite la Abraham Sharp (cca. 1717) este dată de

pi=sum_(k=0)^infty(2(-1)^k3^(1/2-k))/(2k+1)
(9)

(Smith 1953, p. 311). Serii simple suplimentare în care apare pi sunt

.

.

1/4pisqrt(2) = suma_(k=1)^(infty)
(10)
= 1+1/3-1/5-1/7+1/9+1/(11)-...
(11)
1/4(pi-3) = suma_(k=1)^(infty)((-1)^(k+1))/(2k(2k(2k+1)(2k+2))
(12)
= 1/(2-3-4)-1/(4-5-6)+1/(6-7-8)-...
(13)
1/6pi^2 = suma_(k=1)^(infty)1/(k^2)
(14)
= 1+1/4+1/9+1/(16)+1/(25)+...
(15)
1/8pi^2 = suma_(k=1)^(infty)1/((2k-1)^2)
(16)
= 1+1/(3^2)+1/(5^2)+1/(7^2)+....
(17)

(Wells 1986, p. 53).

În 1666, Newton a folosit o construcție geometrică pentru a obține formula

pi = 3/4sqrt(3)+24int_0^(1/4)sqrt(x-x^2)dx
(18)
= (3sqrt(3))/4+24(1/(12)-1/(5-2^5)-1/(28-2^7)-1/(72-2^9)-...),
(19)

care a folosit-o pentru a calcula pi (Wells 1986, p. 50; Borwein et al. 1989; Borwein și Bailey 2003, pp. 105-106). Coeficienții pot fi găsiți din integrala

I(x) = intsqrt(x-x^2)dx
(20)
= 1/4(2x-1)sqrt(x-x^2)-1/8sin^(-1)(1-2x)
(21)

prin extinderea în serie a lui I(x)-I(0)în jurul lui 0, obtaining

I(x)=2/3x^(3/2)-1/5x^(5/2)-1/(28)x^(7/2)-1/(72)x^(9/2)-5/(704)x^(11/2)+...
(22)

(OEIS A054387 și A054388). Folosind transformarea de îmbunătățire a convergenței lui Euler se obține

pi/2 = 1/2sum_(n=0)^(infty)((n!)^22^(n+1))/((2n+1)!!)=sum_(n=0)^(infty)(n!)/((2n+1)!!!)
(23)
= 1+1/3+(1-2)/(3-5)+(1-2-3)/(3-5-7)+...
(24)
= 1+1/3(1+2/5(1+3/7(1+4/9(1+...))))
(25)

(Beeler et al. 1972, poziția 120).

Acest lucru corespunde conectării x=1/sqrt(2) în seria de puteri pentru funcția hipergeometrică _2F_1(a,b;c;x),

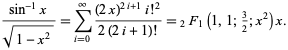(sin^(-1)x)/(sqrt(1-x^2))=sum_(i=0)^infty((2x)^(2i+1)i!^2)/(2(2i+1)!)=_2F_1(1,1;3/2;x^2)x.
(26)

În ciuda îmbunătățirii convergenței, seria (◇) converge la un singur bit/termen. Cu prețul unei rădăcini pătrate, Gosper a observat că x=1/2 dă 2 biți/termen,

1/9sqrt(3)pi=1/2sum_(i=0)^infty((i!)^2)/((2i+1)!),
(27)

și x=sin(pi/10) dă aproape 3.39 biți/termen,

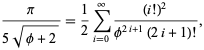pi/(5sqrt(phi+2))=1/2sum_(i=0)^infty((i!)^2)/(phi^(2i+1)(2i+1)(2i+1)!),
(28)

unde phi este raportul de aur. Gosper a mai obținut

pi=3+1/(60)(8+(2-3)/(7-8-3)(13+(3-5)/(10-11-3)(18+(4-7)/(13-14-3)(23+...)))).
(29)

Un algoritm spigot pentru pi este dat de Rabinowitz și Wagon (1995; Borwein și Bailey 2003, pp. 141-142).

Mai uimitor încă, o expresie în formă închisă care dă un algoritm de extragere a cifrelor care produce cifre de pi (sau pi^2) în baza 16 a fost descoperită de Bailey et al. (Bailey et al. 1997, Adamchik și Wagon 1997),

pi=sum_(n=0)^infty(4/(8n+1)-2/(8n+4)-1/(8n+5)-1/(8n+6))(1/(16))^n.
(30)

Această formulă, cunoscută sub numele de formula BBP, a fost descoperită cu ajutorul algoritmului PSLQ (Ferguson et al. 1999) și este echivalentă cu

pi=int_0^1(16y-16)/(y^4-2y^3+4y-4)dy.
(31)

Există o serie de formule de tip BBP pentru pi în puteri ale lui (-1)^k, ale căror prime câteva formule independente sunt

pi = 4sum_(k=0)^(infty)((-1)^k)/(2k+1)
(32)
= 3sum_(k=0)^(infty)(-1)^k
(33)
= 4sum_(k=0)^(infty)(-1)^k
(34)
= sum_(k=0)^(infty)(-1)^k
(35)
= sum_(k=0)^(infty)(-1)^k
(36)
= sum_(k=0)^(infty)(-1)^k.
(37)

În mod similar, există o serie de formule de tip BBP pentru pi în puteri ale lui 2^k, ale căror prime câteva formule independente sunt

.

.

.

.

.

.

pi = suma_(k=0)^(infty)1/(16^k)
(38)
= 1/2sum_(k=0)^(infty)1/(16^k)
(39)
= 1/(16)sum_(k=0)^(infty)1/(256^k)
(40)
= 1/(32)sum_(k=0)^(infty)1/(256^k)
(41)
= 1/(32)sum_(k=0)^(infty)1/(4096^k)
(42)
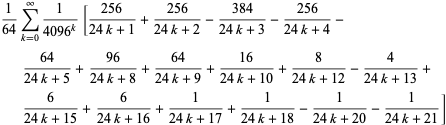= 1/(64)sum_(k=0)^(infty)1/(4096^k)
(43)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(44)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(45)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(46)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k)
(47)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k).
(48)

F. Bellard a găsit formula de tip BBP care converge rapid

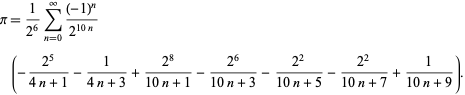pi=1/(2^6)sum_(n=0)^infty((-1)^n)/(2^(10n))(-(2^5)/(4n+1)-1/(4n+3)+(2^8)/(10n+1)-(2^6)/(10n+3)-(2^2)/(10n+5)-(2^2)/(10n+7)+1/(10n+9)).
(49)

O integrală conexă este

pi=(22)/7-.int_0^1(x^4(1-x)^4)/(1+x^2)dx
(50)

(Dalzell 1944, 1971; Le Lionnais 1983, p. 22; Borwein, Bailey și Girgensohn 2004, p. 3; Boros și Moll 2004, p. 125; Lucas 2005; Borwein et al. 2007, p. 14). Această integrală a fost cunoscută de K. Mahler la mijlocul anilor 1960 și apare într-un examen la Universitatea din Sydney în noiembrie 1960 (Borwein, Bailey și Girgensohn, p. 3). Beukers (2000) și Boros și Moll (2004, p. 126) afirmă că nu este clar dacă acestea există o alegere naturală a polinomului rațional a cărui integrală între 0 și 1 produce pi-333/106, unde 333/106 este următoarea convergentă. Totuși, există o integrală pentru a patra convergentă, și anume

pi=(355)/(113)-1/(3164)int_0^1(x^8(1-x)^8(25+816x^2))/(1+x^2)dx.
(51)

(Lucas 2005; Bailey et al. 2007, p. 219). De fapt, Lucas (2005) dă alte câteva astfel de integrale.

Backhouse (1995) a folosit identitatea

.

I_(m,n) = int_0^1(x^m(1-x)^n)/(1+x^2)dx
(52)
= 2^(-(m+n+1))sqrt(pi)Gamma(m+1)Gamma(n+1)×_3F_2(1,(m+1)/2,(m+2)/2;(m+n+2)/2,(m+n+3)/2;-1)
(53)
= a+bpi+cln2
(54)

pentru numerele întregi pozitive m și n și unde a, b, și c sunt constante raționale pentru a genera un număr de formule pentru pi. În special, dacă 2m-n=0 (mod 4), atunci c=0 (Lucas 2005).

O formulă similară a fost descoperită ulterior de Ferguson, ceea ce conduce la o rețea bidimensională de astfel de formule care poate fi generată de aceste două formule date de

pi=sum_(k=0)^infty((4+8r)/(8k+1)-(8r)/(8k+2)-(4r)/(8k+3)-(2+8r)/(8k+4)-(1+2r)/(8k+5)-(1+2r)/(8k+6)+r/(8k+7))(1/(16))^k
(55)

pentru orice valoare complexă a lui r (Adamchik și Wagon), dând formula BBP ca fiind cazul special r=0.

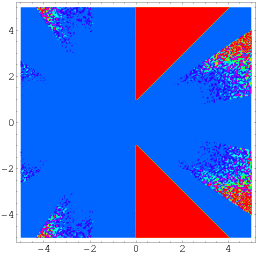
PiFormulasWagonIdentity

O identitate și mai generală datorată lui Wagon este dată de

pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)
(56)

(Borwein și Bailey 2003, p. 141), care este valabil pentru o regiune a planului complex care exclude două porțiuni triunghiulare plasate simetric în jurul axei reale, așa cum este ilustrat mai sus.

O clasă de identități poate chiar mai ciudat de generală este dată de

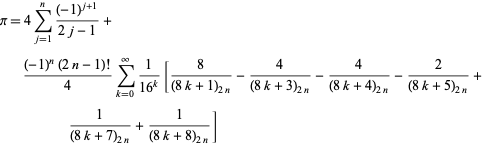pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4sum_(k=0)^infty1/(16^k)
(57)

care este valabil pentru orice număr întreg pozitiv n, unde (x)_n este un simbol Pochhammer (B. Cloitre, com. pers., 23 ianuarie 2005). Chiar mai uimitor, există o formulă strâns analogă pentru logaritmul natural al lui 2.

În urma descoperirii formulei BBP cu cifre în baza 16 și a formulelor înrudite, au fost cercetate formule similare în alte baze. Borwein, Bailey și Girgensohn (2004) au arătat recent că pi nu are o formulă arctangentă BBP de tip Machin care să nu fie binară, deși acest lucru nu exclude o schemă complet diferită pentru algoritmii de extragere a cifrelor în alte baze.

S. Plouffe a conceput un algoritm pentru a calcula a ncea cifră a lui pi în orice bază în O(n^3(logn)^3) pași.

O serie de identități suplimentare datorate lui Ramanujan, Catalan și Newton sunt date de Castellanos (1988ab, pp. 86-88), inclusiv câteva care implică sume de numere Fibonacci. Ramanujan a găsit

sum_(k=0)^infty((-1)^k(4k+1)^3)/(^3)=sum_(k=0)^infty((-1)^k(4k+1)^3)/(pi^(3/2)^3)=2/pi
(58)

(Hardy 1923, 1924, 1999, p. 7).

Plouffe (2006) a găsit frumoasa formulă

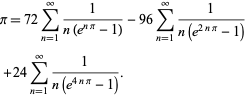pi=72sum_(n=1)^infty1/(n(e^(npi)-1))-96sum_(n=1)^infty1/(n(e^(2npi)-1)) +24sum_(n=1)^infty1/(n(e^(4npi)-1)).
(59)

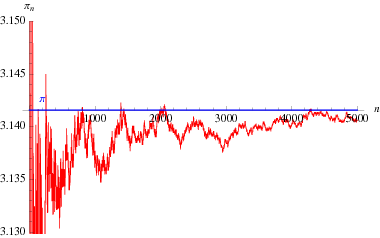
PiBlatnerProduct

O formulă interesantă de produs infinit datorată lui Euler care leagă pi și al nlea prim p_n este

.

.

pi = 2/(produs_(n=1)^(infty))
(60)
= 2/(product_(n=2)^(infty))
(61)

(Blatner 1997, p. 119), reprezentată mai sus în funcție de numărul de termeni din produs.

O metodă similară cu cea a lui Arhimede poate fi folosită pentru a estima pi, începând cu un n-gon și apoi raportând aria următoarelor 2n-gonuri. Fie beta unghiul de la centrul unuia dintre segmentele poligonului,

beta=1/4(n-3)pi,
(62)

atunci

pi=(2sin(2beta))/((n-3)product_(k=0)^(infty)cos(2^(-k)beta))
(63)

(Beckmann 1989, pp. 92-94).

Vieta (1593) a fost primul care a dat o expresie exactă pentru pi luând n=4 în expresia de mai sus, obținând

cosbeta=sinbeta=1/(sqrt(2))=1/2sqrt(2),
(64)

care conduce la un produs infinit de radicali imbricați,

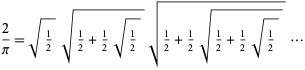2/pi=sqrt(1/2)sqrt(1/2+1/2sqrt(1/2))sqrt(1/2+1/2sqrt(1/2))sqrt(1/2+1/2sqrt(1/2)))...
(65)

(Wells 1986, p. 50; Beckmann 1989, p. 95). Cu toate acestea, nu s-a dovedit riguros că această expresie converge până la Rudio în 1892.

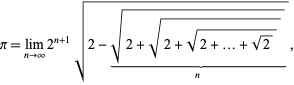
O formulă înrudită este dată de

pi=lim_(n-infty)2^(n+1)sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2+...+sqrt(2))))_()_(n)),
(66)

ceea ce se poate scrie

pi=lim_(n-infty)2^(n+1)pi_n,
(67)

unde pi_n se definește folosind iterația

pi_n=sqrt((1/2pi_(n-1))^2+^2)
(68)

cu pi_0=sqrt(2) (J. Munkhammar, com. pers, 27 aprilie 2000). Formula

pi=2lim_(m-infty)sum_(n=1)^msqrt(^2+1/(m^2))
(69)

este, de asemenea, strâns legată.

O formulă drăguță pentru pi este dată de

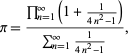pi=(produs_(n=1)^(infty)(1+1/(4n^2-1)))/(sumă_(n=1)^(infty)1/(4n^2-1)),
(70)

unde numărătorul este o formă a formulei Wallis pentru pi/2 iar numitorul este o sumă telescopată cu suma 1/2 deoarece

1/(4n^2-1)=1/2(1/(2n-1)-1/(2n+1))
(71)

(Sondow 1997).

Un caz particular al formulei Wallis dă

pi/2=product_(n=1)^infty=(2-2)/(1-3)(4-4)/(3-5)(6-6)/(5-7)...
(72)

(Wells 1986, p. 50). Această formulă poate fi, de asemenea, scrisă

lim_(n-infty)(2^(4n))/(n(2n; n)^2)=pilim_(n-infty)(n^2)/(^2)=pi,
(73)

unde (n; k) denotă un coeficient binomial și Gamma(x) este funcția gamma (Knopp 1990). Euler a obținut

pi=sqrt(6(1+1/(2^2)+1/(3^2)+1/(4^2)+...)),
(74)

ceea ce rezultă din valoarea specială a funcției zeta Riemann zeta(2)=pi^2/6. Formule similare rezultă din zeta(2n) pentru toți numerele întregi pozitive n.

O sumă infinită datorată lui Ramanujan este

1/pi=sum_(n=0)^infty(2n; n)^3(42n+5)/(2^(12n+4))
(75)

(Borwein et al. 1989; Borwein și Bailey 2003, p. 109; Bailey et al.2007, p. 44). Alte sume sunt date în Ramanujan (1913-14),

4/pi=sum_(n=0)^infty((-1)^n(1123+21460n)(2n-1)!!!(4n-1)!!!)/(882^(2n+1)32^n(n!)^3)
(76)

și

1/pi = sqrt(8)sum_(n=0)^(infty)((1103+26390n)(2n-1)!!(4n-1)!!)/(99^(4n+2)32^n(n!)^3)
(77)
= (sqrt(8))/(9801)sum_(n=0)^(infty)((4n)!(1103+26390n))/((n!)^4396^(4n))
(78)

(Beeler et al. 1972, poziția 139; Borwein et al. 1989; Borwein și Bailey 2003, p. 108; Bailey et al. 2007, p. 44). Ecuația (78) este derivată dintr-o identitate modulară de ordinul 58, deși o primă derivare nu a fost prezentată înainte de Borwein și Borwein (1987). Seriile de mai sus dau ambele

pi aprox (9801)/(2206sqrt(2))=3,14159273001...
(79)

(Wells 1986, p. 54) ca primă aproximație și oferă, respectiv, aproximativ 6 și 8 zecimale pe termen. Astfel de serii există datorită raționalității diverșilor invarianți modulari.

Forma generală a seriei este

sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)1/(^n)=(sqrt(-j(t)))/pi,
(80)

unde t este discriminantul unei forme pătratice binare, j(t) este funcția j,

.

b(t) = sqrt(t)
(81)
a(t) = (b(t))/6{1-(E_4(t))/(E_6(t))},
(82)

și E_i sunt serii Eisenstein. Un câmp de numere de clasă p implică numere întregi algebrice de plea grad ale constantelor A=a(t), B=b(t), și C=c(t). Dintre toate seriile formate numai din termeni întregi, cea care dă cele mai multe cifre numerice în cel mai scurt timp corespunde celui mai mare discriminant al clasei numărul 1 de d=-163 și a fost formulată de frații Chudnovsky (1987). Numărul 163 care apare aici este același cu cel care apare în faptul că e^(pisqrt(163)) (constanta lui Ramanujan) este foarte aproape de un număr întreg. În mod similar, factorul 640320^3 provine din identitatea funcției j pentru j(1/2(1+isqrt(163))). Seria este dată de

1/pi = 12sum_(n=0)^(infty)((-1)^n(6n)!(13591409+545140134n))/((n!)^3(3n)!(640320^3)^(n+1/2))
(83)
= (163·8·27·7·11·19·127)/(640320^(3/2))sum_(n=0)^(infty)((13591409)/(163·2·9·7·11·19·127)+n)((6n)!)/((3n)!(n!)^3)((-1)^n)/(640320^(3n))
(84)

(Borwein și Borwein 1993; Beck și Trott; Bailey et al. 2007, p. 44). Această serie oferă 14 cifre cu exactitate pe termen. Aceeași ecuație într-o altă formă a fost dată de frații Chudnovsky (1987) și este utilizată de limbajul Wolfram pentru a calcula pi (Vardi 1991; Wolfram Research),

pi=(426880sqrt(10005))/(A),
(85)

unde

.

A = 13591409
(86)
B = -1/(151931373056000)
(87)
C = (30285563)/(1651969144908540723200).
(88)

Cea mai bună formulă pentru clasa numărul 2 (cel mai mare discriminant -427) este

1/pi=12sum_(n=0)^infty((-1)^n(6n)!(A+Bn))/((n!)^3(3n)!C^(n+1/2)),
(89)

unde

.

A = 212175710912sqrt(61)+1657145277365
(90)
B = 13773980892672sqrt(61)+107578229802750
(91)
C = ^3
(92)

(Borwein și Borwein 1993). Această serie adaugă aproximativ 25 de cifre pentru fiecare termen suplimentar. Seria care converge cel mai rapid pentru clasa numărul 3 corespunde la d=-907 și oferă 37-38 de cifre pentru fiecare termen. Seria cu cea mai rapidă convergență pentru clasa numărul 4 corespunde lui d=-1555 și este

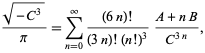(sqrt(-C^3))/pi=sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)(A+nB)/(C^(3n)),
(93)

unde

.

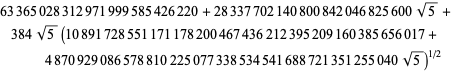A = 63365028312971999585426220+28337702140800842046825600sqrt(5)+384sqrt(5)(10891728551171178200467436212395209160385656017+4870929086578810225077338534541688721351255040sqrt(5))^(1/2)
(94)
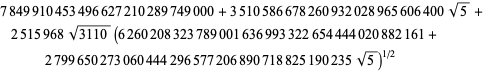B = 7849910453496627210289749000+3510586678260932028965606400sqrt(5)+2515968sqrt(3110)(6260208323789001636993322654444020882161+2799650273060444296577206890718825190235sqrt(5))^(1/2)
(95)
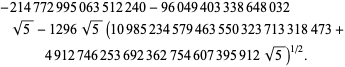C = -214772995063512240-96049403338648032sqrt(5)-1296sqrt(5)(10985234579463550323713318473+4912746253692362754607395912sqrt(5))^(1/2).
(96)

Aceasta dă 50 de cifre pe termen. Borwein și Borwein (1993) au dezvoltat un algoritm general pentru generarea unor astfel de serii pentru un număr arbitrar de clase.

O listă completă a seriilor lui Ramanujan pentru 1/pi găsite în al doilea și al treilea caiet al său este dată de Berndt (1994, pp. 352-354),

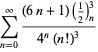4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(97)
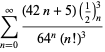(16)/pi = sum_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(98)
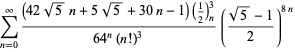(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(99)
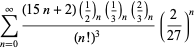(27)/(4pi) = sum_(n=0)^(infty)((15n+2)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(2/(27))^n
(100)
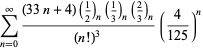(15sqrt(3))/(2pi) = sum_(n=0)^(infty)((33n+4)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(4/(125))^n
(101)
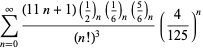(5sqrt(5))/(2pisqrt(3)) = sum_(n=0)^(infty)((11n+1)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(125))^n
(102)
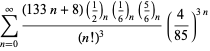(85sqrt(85))/(18pisqrt(3)) = sum_(n=0)^(infty)((133n+8)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(85))^(3n)
(103)
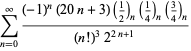4/pi = sum_(n=0)^(infty)((-1)^n(20n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^32^(2n+1))
(104)
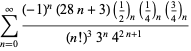4/(pisqrt(3)) = sum_(n=0)^(infty)((-1)^n(28n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^33^n4^(2n+1))
(105)
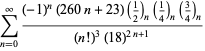4/pi = sum_(n=0)^(infty)((-1)^n(260n+23)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(18)^(2n+1))
(106)
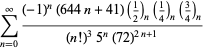4/(pisqrt(5)) = sum_(n=0)^(infty)((-1)^n(644n+41)(1/2)_n(1/4)_n(3/4)_n)/((n!)^35^n(72)^(2n+1))
(107)
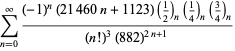4/pi = sum_(n=0)^(infty)((-1)^n(21460n+1123)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(882)^(2n+1))
(108)
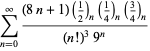(2sqrt(3))/pi = sum_(n=0)^(infty)((8n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^n)
(109)
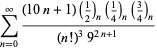1/(2pisqrt(2)) = sum_(n=0)^(infty)((10n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^(2n+1))
(110)
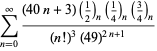1/(3pisqrt(3)) = sum_(n=0)^(infty)((40n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(49)^(2n+1))
(111)
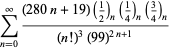2/(pisqrt(11)) = sum_(n=0)^(infty)((280n+19)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(2n+1))
(112)
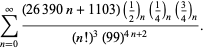1/(2pisqrt(2)) = sum_(n=0)^(infty)((26390n+1103)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(4n+2)).
(113)

Aceste ecuații au fost demonstrate pentru prima dată de Borwein și Borwein (1987a, pp. 177-187). Borwein și Borwein (1987b, 1988, 1993) au demonstrat și alte ecuații de acest tip, iar Chudnovsky și Chudnovsky (1987) au găsit ecuații similare pentru alte constante transcendentale (Bailey et al. 2007, pp. 44-45).

O listă completă a ecuațiilor independente cunoscute de acest tip este dată de

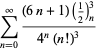4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(114)
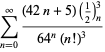(16)/pi = sum_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(115)
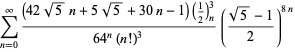(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(116)
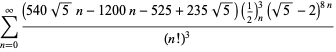(5^(1/4))/pi = sum_(n=0)^(infty)((540sqrt(5)n-1200n-525+235sqrt(5))(1/2)_n^3(sqrt(5)-2)^(8n))/((n!)^3)
(117)
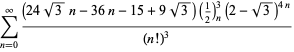(12^(1/4))/pi = suma_(n=0)^(infty)((24sqrt(3)n-36n-15+9sqrt(3))(1/2)_n^3(2-sqrt(3))^(4n))/((n!)^3)
(118)

pentru m=1 cu semne nealternante,

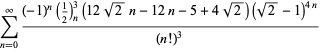2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(12sqrt(2)n-12n-5+4sqrt(2))(sqrt(2)-1)^(4n))/((n!)^3)
(119)
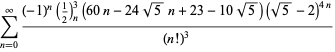2/pi = suma_(n=0)^(infty)((-1)^n(1/2)_n^3(60n-24sqrt(5)n+23-10sqrt(5))(sqrt(5)-2)^(4n))/((n!)^3)
(120)
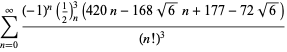2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(420n-168sqrt(6)n+177-72sqrt(6)))/((n!)^3)
(121)
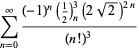(2sqrt(2))/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(2sqrt(2))^(2n))/((n!)^3)
(122)

pentru m=1 cu semne alternative,

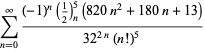(128)/(pi^2) = suma_(n=0)^(infty)((-1)^n(1/2)_n^5(820n^2+180n+13))/(32^(2n)(n!)^5)
(123)
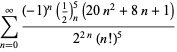(32)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(20n^2+8n+1))/(2^(2n)(n!)^5)
(124)

pentru m=2 (Guillera 2002, 2003, 2006),

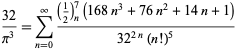(32)/(pi^3)=sum_(n=0)^infty((1/2)_n^7(168n^3+76n^2+14n+1))/(32^(2n)(n!)^5)
(125)

pentru m=3 (Guillera 2002, 2003, 2006), și nu se cunosc altele pentru m3 (Bailey et al. 2007, pp. 45-48).

Bellard dă formula exotică

pi=1/(740025),
(126)

where

P(n)=-885673181n^5+3125347237n^4-2942969225n^3+1031962795n^2-196882274n+10996648.
(127)

Gasper citează rezultatul

pi=(16)/3^(-1),
(128)

unde _1F_2 este o funcție hipergeometrică generalizată, și o transformă în

pi=lim_(x-infty)4x_1F_2(1/2;3/2,3/2;-x^2).
(129)

Un rezultat fascinant datorat lui Gosper este dat de

lim_(n-infty)product_(i=n)^(2n)pi/(2tan^(-1)i)=4^(1/pi)=1,554682275....
(130)

pi satisface inegalitatea

(1+1/pi)^(pi+1) aprox. 3,14097pi.
(131)

D. Terr (com. pers.) a remarcat curioasa identitate

(3,1,4)=(1,5,9)+(2,6,5) (mod 10)
(132)

care implică primele 9 cifre ale lui pi.

.

Lasă un răspuns

Adresa ta de email nu va fi publicată.