Proporționalul este doar un mod de a reacționa la o eroare în sistem. Problema cu controlul proporțional este că nu poate detecta tendințele și nu se poate adapta la ele. Aceasta este treaba controlului integral.
Există un alt exemplu de grafic al erorii unui sistem în timp în partea stângă a figurii 6. Din nou, ar putea fi distanța unui robot față de un obiect, sau ar putea fi nivelul lichidului dintr-un rezervor, sau temperatura din cuptorul unei fabrici. Poate că ținta pe care robotul o urmărește continuă să se îndepărteze de robot cu o viteză pe care robotul nu o poate prinde din urmă. Poate că garnitura ușii cuptorului este uzată; poate că prelevarea de lichid din rezervor este neobișnuit de mare. Indiferent de cauză, deoarece proporționalul nu este proiectat să reacționeze la tendințe, nu poate detecta și corecta problema. Aici intră în scenă controlul integral.
Integral măsoară aria dintre valorile de eroare și axa timpului. Dacă eroarea nu revine la zero, aria erorii devine din ce în ce mai mare. Partea dreaptă a figurii 6 arată modul în care ieșirea integrală poate reacționa la acest tip de tendință. Pe măsură ce aria dintre curba erorii și axa timpului crește, ieșirea crește proporțional cu această arie. Ca urmare, ieșirea acționează actuatorul din ce în ce mai greu pentru a corecta eroarea.
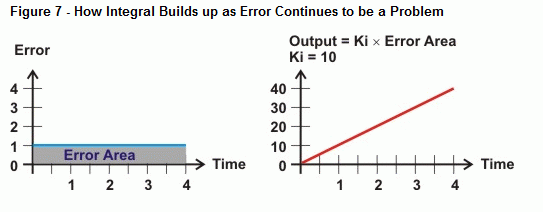
Atunci ce se întâmplă când eroarea nu este o linie dreaptă, precum curba prezentată în figura 8? Asta este ceea ce determină operația de calcul de integrare, aria dintre o curbă și o axă. În cazul controlului integral, pe măsură ce trece mai mult timp cu o eroare, aria de sub curbă crește, la fel și valoarea pe care calculul integral o va folosi pentru a conduce împotriva erorii sistemului. Dacă curba de eroare coboară sub axa timpului, acumularea de suprafață negativă se scade din acumularea de suprafață pozitivă. Atunci când este reglat corect, controlul integral poate ajuta sistemul să se axeze pe o eroare de zero.
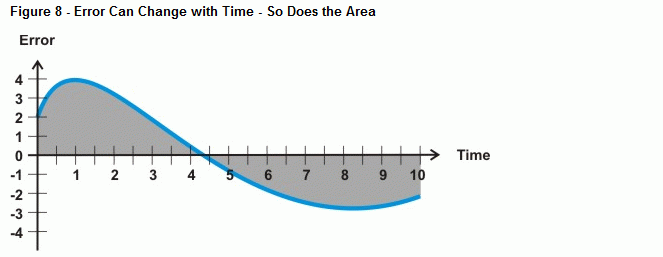
Stampila BASIC poate aproxima eroarea sub curbă cu integrare numerică. Figura 9 arată cum puteți aproxima eroarea sub o curbă prin însumarea suprafeței unei grămezi de dreptunghiuri mici între curba de eroare și axa timpului. Aria fiecărei cutii reprezintă eroarea înmulțită cu timpul dintre măsurători. Adăugând toate suprafețele cutiilor, obțineți o aproximare a suprafeței sub curbă.
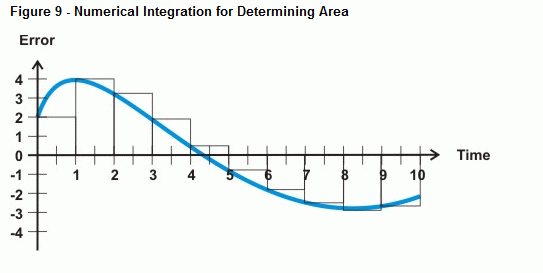
Atâta timp cât măsurătorile dvs. sunt distanțate uniform, puteți numi lățimea fiecărei cutii o valoare de 1. Acest lucru face ca matematica să fie mult mai simplă decât să încercați să țineți cont de 20 ms între eșantioane, 5 minute între eșantioane sau oricare ar fi rata de eșantionare care se dovedește a fi. În loc să înmulțiți eroarea cu incrementul de timp dintre eșantioane și apoi să adăugați la următoarea eroare înmulțită cu timpul, puteți înmulți pur și simplu fiecare eșantion de eroare cu un timp de 1. Rezultatul este că puteți pur și simplu să păstrați un total curent de măsurători de eroare pentru calculul integral. Iată un exemplu despre cum se poate face acest lucru cu PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
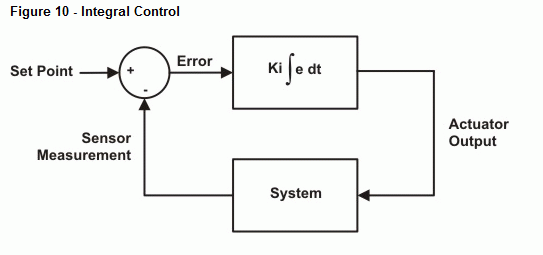
Programul de exemplu următor realizează integrarea numerică pe semnalul de eroare și ajustează ieșirea în consecință. Ca și în cazul controlului proporțional, există o constantă care scalează ieșirea de integrare la valoarea dorită. De dragul simplității, vom folosi din nou 10 pentru Ki. Figura 10 prezintă o schemă bloc a buclei de control. Termenul Kp ∫ edt se referă la Kp înmulțit cu integrala erorii în timp. Cu alte cuvinte, Kp înmulțit cu aria acumulată între curba erorii și axa timpului.
Program de exemplu – IntegralAlgorithm.bs2
- Introduceți, salvați și rulați IntegralAlgorithm.bs2.
- Introduceți această secvență de valori în fereastra de transmisie a terminalului de depanare: 3 3 3 3 3 3 3 3 3. Observați cum ieșirea integrală devine mai mare de fiecare dată când se repetă 3. Aceasta este treaba integralei, să detecteze tendințele și să mărească unitatea pentru a o corecta după cum este necesar.
- Încercați acum această secvență: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. Aria de sub această curbă este 0, deoarece aria negativă este aceeași cu cea pozitivă. Acesta este, de asemenea, rezultatul la care va ajunge calculul integral după ce ați terminat de introdus secvența.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Cum funcționează IntegralAlgorithm.bs2
Acest program este un ProportionalAlgorithm.bs2 modificat pentru a efectua în schimb calculul integral. Există acum două tipuri diferite de erori care trebuie urmărite, așa că acolo matricea variabilei de erori a fost extinsă la două elemente. Variabila error(0) urmărește eroarea curentă, iar error(1) urmărește eroarea acumulată. Constantele Current CON 0 și Accumulator CON 1 fac evidența contabilă un pic mai sensibilă cu error(current) și error(accumulator).
O altă modificare care a fost făcută este că eroarea este acumulată și ieșirea integrală este calculată cu aceste două instrucțiuni:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Your Turn – Clamping the Integral Output
După cum probabil v-ați dat seama introducând în mod repetat 3 în Debug Terminal, ieșirea integrală a acționării poate începe cu adevărat să fugă. Puteți utiliza operatorii MIN și MAX pentru a împiedica comanda integrală să exagereze cu ieșirea. Să repetăm activitatea de decalaj servo și să limităm ieșirea de la 650 la 850.
- Schimbați instrucțiunea drive = i în drive = i + Offset MIN 650 MAX 850.
- Executați programul și verificați că ieșirea integrală este limitată la valori între 650 și 850. Încercați să introduceți 2 în mod repetat, apoi -2 în mod repetat.
.