Cum să te pregătești pentru întrebările de geometrie de la testul de matematică
Informații generale
Geometria este doar un nume sofisticat pentru studiul liniilor și al formelor. Există cu siguranță principii și subiecte dificile suplimentare, dar avem aici elementele de bază. Va trebui să le stăpâniți pe acestea înainte de a aborda concepte mai avansate.
(Vă rugăm să rețineți că, dacă o figură este etichetată „exemplu” în acest ghid, este posibil să nu fie singura reprezentare a acelei figuri, dar este una dintre ele.)
Puncte și linii
Un punct în geometrie este o locație. El nu are lungime, lățime sau adâncime. Folosim un punct și o literă majusculă pentru a arăta un punct.
Un segment de dreaptă este definit de două puncte și de toate punctele dintre ele. Cele două puncte se numesc puncte terminale ale segmentului. Un segment are o singură dimensiune: lungimea. Pentru a scrie un segment, plasați o bară peste cele două puncte terminale. \(\(\supralinia{AB}\) sau \(\(\supralinia{BA}\) este acest segment:

O dreaptă se întinde în ambele direcții fără capăt. Pentru a scrie o linie, se plasează o bară cu două săgeți deasupra oricăror două puncte ale liniei. \(\(\spre săgeata stânga-dreapta{AB}\) sau \(\(\spre săgeata stânga-dreapta{BA}\) este linia:

O rază începe de la un punct final și se întinde fără sfârșit într-o singură direcție. Pentru a scrie o rază, plasați o bară cu o săgeată îndreptată spre dreapta peste două puncte: punctul final și orice alt punct (în direcția respectivă). \(\(\asupra săgeții spre dreapta{AB}\) este raza:

Nota: nu se poate scrie o rază cu săgeata îndreptată spre stânga, cum ar fi \(\asupra săgeții spre stânga{BA}\). De asemenea, ordinea este importantă. \(\(\spre dreapta săgeată{BA}\) nu este același lucru cu \(\(\spre dreapta săgeată{AB}\). Prima literă este întotdeauna punctul de plecare al unei raze.
Două drepte, segmente sau raze sunt perpendiculare dacă formează un unghi drept (vezi mai jos). Folosiți simbolul \(\perp\) pentru a denota perpendicularitatea. De exemplu, dacă \(\(\sobrelinia{AB}\) este perpendiculară pe \(\(\supralinia{CD}\), se poate scrie \(\(\supralinia{AB} \perp \supralinia{CD}\).
Exemple: 
Două drepte sunt paralele dacă nu se intersectează niciodată. Dacă \(\(\spre dreapta-sus săgeată stângă{AB}\) este paralelă cu \(\(\spre dreapta-sus săgeată stângă{CD}\), se poate scrie \(\spre dreapta-sus săgeată stângă{AB} \paralelă \spre dreapta-sus săgeată stângă{CD}\).
Exemple: 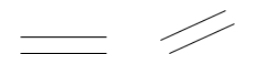
Forme plane
În geometrie, un plan este o suprafață plană bidimensională care se extinde la infinit. Cele două dimensiuni sunt lungimea și lățimea. Așadar, formele plane sunt forme „plate”, cum ar fi pătratele, cercurile și triunghiurile.
Forme comune
Un poligon este o suprafață închisă pe un plan delimitată de segmente de dreaptă numite laturi.
Exemple: 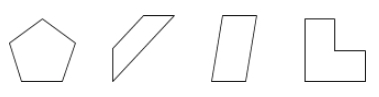
Un poligon regulat este un poligon în care toate segmentele și unghiurile interioare sunt congruente.
Exemple:
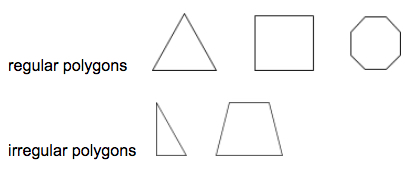
Un triunghi este un poligon cu trei laturi.
Exemple:
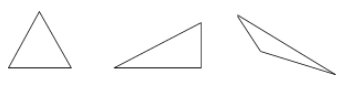
Quadrilateralele – poligoane cu patru laturi
Un paralelogram este un tip de paralelogram în care laturile opuse sunt paralele și congruente. Unghiurile opuse ale unui paralelogram sunt, de asemenea, congruente.
Exemple: 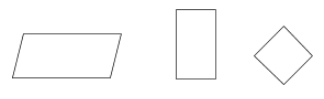
Un dreptunghi este un paralelogram cu patru unghiuri drepte.
Exemple: 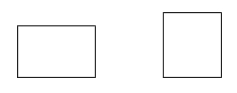
Un romb este un paralelogram în care toate cele patru laturi sunt congruente.
Exemple: 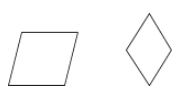
Un pătrat este un paralelogram care este atât un romb cât și un dreptunghi (toate laturile sunt congruente și toate unghiurile sunt drepte).
Exemple: 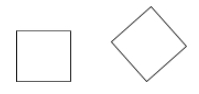
Un trapez este un patrulater cu o singură pereche de laturi paralele.
Exemple: 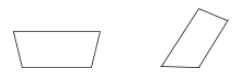
Poligoane cu mai mult de patru laturi
\
\(^1\) Un poligon cu 11 laturi poate fi numit și endecagon sau undecagon.
Măsurarea formelor
Perimetrul este distanța totală în jurul unui poligon. Pentru a afla perimetrul, trebuie doar să adunăm lungimile tuturor laturilor. Dacă poligonul este regulat (toate laturile sunt congruente) și lungimea unei laturi este \(s\), atunci înmulțiți numărul de laturi cu \(s\) pentru a afla perimetrul. De exemplu, perimetrul unui pentagon regulat este \(P_\text{reg pentagon}=5s\)
.