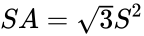Pentru revista academică, vezi Tetrahedron (revistă).
| Tetraedru regulat | ||
|---|---|---|
 (Click aici pentru modelul rotativ) |
||
| Tip | Solid platonic | |
| Elemente | F = 4, E = 6 V = 4 (χ = 2) |
|
| Fațe de laturi | 4{3} | |
| Simbolul Schläfli | {3,3} și s{2,2} | |
| Simbolul lui Wythoff | 3 | 2 3 | 2 2 2 2 |
|
| Coxeter-Dynkin | |
|
| Simetrie | Td sau (*332) |
|
| U01, C15, W1 | ||
| Proprietăți | Deltaedru convex regulat | |
| Unghiul diedru | 70.528779° = arccos(1/3) | |
 3.3.3 (figură cu vârfuri) |
 Autoduală (poliedru dual) |
|
 Net |
||
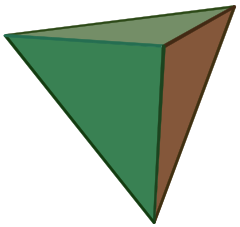
Un tetraedru (plural: tetraedre) este un poliedru compus din patru fețe triunghiulare, dintre care trei se întâlnesc la fiecare vârf. Un tetraedru regulat este un tetraedru în care cele patru triunghiuri sunt regulate sau „echilaterale” și este unul dintre solidele platonice.
Tetraedrul este un tip de piramidă, care este un poliedru cu o bază poligonală plană și fețe triunghiulare care leagă baza de un punct comun. În cazul tetraedrului, baza este un triunghi (oricare dintre cele patru fețe poate fi considerată bază), astfel că tetraedrul mai este cunoscut și sub numele de piramidă triunghiulară sau deltaedru digonal.
Formule pentru tetraedrul regulat
Volumul este
Suprafața este
Template:Commonscat
- F. M. Jackson și Weisstein, Eric W., „Tetrahedron” din MathWorld.
- Weisstein, Eric W., „Tetrahedron” din MathWorld.
- Weisstein, Eric W., „Tetrahedron” din MathWorld.
- The Uniform Polyhedra
- Tetrahedron: Interactive Polyhedron Model
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Formula lui Piero della Francesca pentru volumul tetraedrului la MathPages
- Modeluri gratuite pe hârtie ale unui tetraedru și ale multor alte poliedre
- An Amazing, Space Filling, Non-regular Tetrahedron care include, de asemenea, o descriere a unui „inel rotativ de tetraedre”, cunoscut și sub numele de kaleidocycle.
- Rețea de bază tetraedrică Aplicarea unei structuri tetraedrice pentru a crea o rețea de date rezilientă cu ochiuri parțiale
- Formule exacte explicite pentru tensorul de inerție al unui tetraedru arbitrar în funcție de coordonatele vârfurilor sale
- Tensorul de inerție al unui tetraedru
.