Introducere
Transformările de coordonate sunt destul de neintuitive în 2-D și destul de dureroase în 3-D. Această pagină le abordează în următoarea ordine: (i) vectori în 2-D, (ii) tensori în 2-D, (iii) vectori în 3-D, (iv) tensori în 3-D și, în cele din urmă(v) transformări tensoriale de rang 4.
Un aspect major al transformărilor de coordonate este evaluarea matricei de transformare, în special în 3-D. Acest aspect este abordat aici și discutat pe larg pe pagina următoare.
Este foarte important să recunoaștem că toate transformările de coordonate de pe această pagină sunt rotații ale sistemului de coordonate, în timp ce obiectul în sine rămâne fix. „Obiectul” poate fi un vector, cum ar fi forța sau viteza, sau un tensor, cum ar fi tensiunea sau deformația într-o componentă. Rotațiile obiectului sunt discutate în secțiunile ulterioare.
Transformări în coordonate 2-D ale vectorilor
Patatul academic oferă un exemplu excelent de modul în care transformările de coordonate se aplică vectorilor, subliniind în același timp că sistemul de coordonate este cel care se rotește și nu vectorul… sau cartoful.
Patatul din stânga are un vector pe el. Dar fără un sistem de coordonate, nu există nici o modalitate de a descrie vectorul.Deci, un sistem de coordonate a fost adăugat la cartof, așa cum se arată în dreapta, permițând ca vectorul să fie descris acum ca \({\bf v} = 2{\bf i} + 9{\bf j}\).

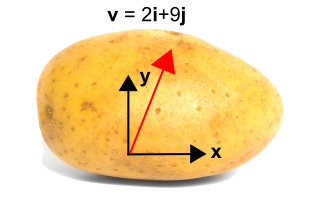

Acum introducem un sistem de coordonate rotit arătat în albastru mai jos, folosind \(x’\) și \(y’\). Noul sistem este rotit în sens invers acelor de ceasornic cu un unghi, \(\theta\),față de sistemul de coordonate inițial. Observați că vectorul în sine nu se schimbă deloc. Este în continuare același vector ca și înainte. Dar este descris de valori numerice diferite în noul sistem de coordonate. În acest caz, vectorul este mai strâns paralel cu noua axă \(x’\) decât cu axa \(y’\), astfel încât componenta \({\bf i’}\) va fi mai mare decât componenta \({\bf j’}\). Transformarea este dată sub figură.
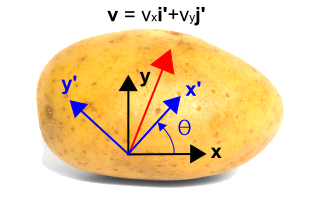
\\\
Acest lucru poate fi observat observând căCei patru factori alcătuiesc cei patru termeni din ecuațiile transformării. Aceștia sunt ușor de verificat prin setarea \(\theta = 0^\circ \) și \(\theta = 90^\circ \). Când \(\theta = 0^\circ\), atunci \(v’_x = v_x\) și \(v’_y = v_y\). Când \(\theta = 90^\circ\), atunci \(v’_x = v_y\) și \(v’_y = -v_x\).
Matrice de transformare
Este mai convenabil să scriem (și să lucrăm cu) ecuațiile de transformare folosind matrici.
\left\{ \matrix {v_x \\\ v_y} \right\\}\]
Termenii \(\cos \theta\) sunt pe diagonala matricei, în timp ce termenii \(\sin \theta\) sunt în afara diagonalei. Singura problemă potențială este să vă amintiți care termen \(\sin \theta\) are semnul minus. Acesta este întotdeauna termenul din stânga jos.
Ecuația de mai sus se scrie în notație matricială sub forma
\
unde \({\bf Q}\) este litera obișnuită aleasă pentru matricea de transformare.

Matrice de transformare vs. matrice de rotație
Dacă acest subiect nu era deja destul de dificil, multe cărți și site-uri web sporesc confuzia prin faptul că nu clarifică ce este fix și ce este rotație. În această pagină și în următoarea, sistemul de coordonate este cel care se rotește, în timp ce obiectul rămâne fix.Așadar, termenul de matrice de transformare este folosit aici pentru a sublinia acest lucru.
Cu toate acestea, vom aborda mai târziu situațiile în care obiectul se rotește în timp ce sistemul de coordonate rămâne fix. În acest scenariu, termenul matrice de rotație va fi folosit pentru a sublinia faptul că obiectul se rotește.
Multă confuzie apare din cauza faptului uimitor că fiecare matrice (transformare și rotație) este doar transpunerea celeilalte! Așadar, ele arată extrem de asemănător. În problemele bidimensionale,singura diferență practică este dacă semnul minus din fața lui \(\sin \theta\) se află pe termenul \(q_{12}\) sau pe termenul \(q_{21}\).
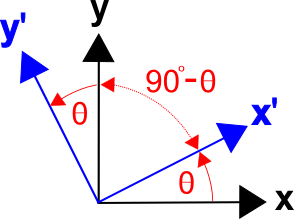
Există o metodă generală de formulare a matricelor de transformare bazată pe cosinusurile unghiurilor dintre axele celor două sisteme de coordonate, adică pe cosinusurile de direcție. (Acest lucru este valabil și pentru transformările 3D.)Matricea de transformare poate fi scrisă sub forma
\\\]
unde \((x’,x)\) reprezintă unghiul dintre axele \(x’\) și \(x\),\((x’,y)\) este unghiul dintre axele \(x’\) și \(y\), etc.
Unghiul dintre \(x’\) și \(y\) este \((90^\circ – \theta)\), iar \(\cos(x’,y) = \cos(90^\circ – \theta) = \sin \theta\).
La fel, unghiul dintre \(y’\) și \(x\) este \((90^\circ + \theta)\), iar \(\cos(y’,x) = \cos(90^\circ + \theta) = -\sin \theta\).
Notație tensorială
Transformarea coordonatelor se scrie în notație tensorială sub forma
\
unde \(\lambda_{ij}\) este matricea de transformare \({\bf Q}\). (Nu știu de ce se folosește \({\bf Q}\) în notația matricială, dar în notația tensorială se folosește \(\lambda_{ij}\), nu \(q_{ij}\).) \(\(\lambda_{ij}\) se definește ca
\
De exemplu, dacă \(i = 1\) și \(j = 2\), atunci
\
\(\lambda_{ij}\) este cosinusul de direcție al unghiului dintre axa \(x’_i\) și axa \(x_j\). Din nou, acest lucru este la fel de aplicabil și la transformările 3-D.
Transformări în coordonate 2-D ale tensorilor
Această secțiune va prezenta ce și cum ale transformărilor tensoriale.De ce-ul va trebui să aștepte până mai târziu.
Transformările în coordonate ale tensorilor de rangul 2 implică aceeași matrice \({\bf Q}\) ca și transformările vectoriale. O transformare a tensorului de tensiune, \(\boldsymbol{\sigma}\),din sistemul de coordonate de referință \(x-y\) în \(\boldsymbol{\sigma’}\) într-un nou sistem \(x’-y’\) se face după cum urmează.
\
Scriind matricile în mod explicit se obține
\ = \left \left \left \left \]
(Rețineți că tensorul de tensiuni este întotdeauna simetric, chiar și în urma transformărilor.)
Multiplicând matricile se obține
\
Aceste trei ecuații sunt exact transformarea 2-D a unui tensor de tensiuni care rezultă din însumarea forțelor asupra unui element diferențial și impunerea echilibrului. Aceasta este, de asemenea, reprezentată de cercul lui Mohr.
Notație tensorială
Transformarea coordonatelor se scrie în notație tensorială sub forma
\
Ca de obicei, notația tensorială oferă o perspectivă suplimentară asupra procesului. De data aceasta, înțelegerea provine din subscriptele de pe lambdas. Fiecare lambda împerechează efectiv un subscript de pe \(\boldsymbol{\sigma’}\) cu unul de pe \(\boldsymbol{\sigma}\).Acest lucru este valabil indiferent de rangul tensorului.
Transformările în coordonate 3-D ale vectorilor
Multe dintre ecuațiile generale utilizate în transformările 2-D sunt aplicabile și în 3-D.Exemplele includ
\
Doar acum detaliile sunt diferite. Vectorii au componente z și matricele de transformare sunt 3×3 în loc de 2×2.
\\\]
\\]
\ \left\{ \matrix { v_x \\\ v_y \\\\ v_z } \right\\}\]
Transformări în coordonate 3D ale tensorilor
Încă o dată, regulile nu se schimbă, doar particularitățile se schimbă.
\
Scriind matricile în mod explicit se obține
\ = \left\left\left\left\\]
Această pagină web efectuează transformări de coordonate pe tensori 3D. Încercați-o.
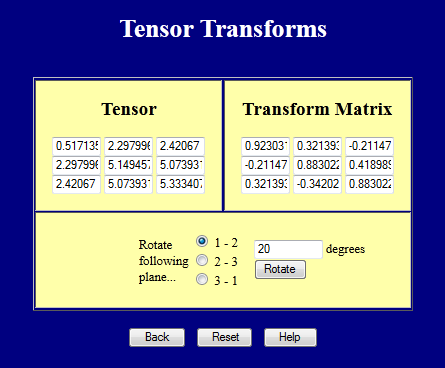
Transformări de coordonate ale tensorilor de rangul 4
Vom vedea în secțiunea despre Legea lui Hooke că tensorul de rigiditate este de rangul 4, adică 3x3x3x3 (nu 4×4). Este scris sub forma \(C_{ijkl}\) deoarece leagă orice componentă de deformație, \(\epsilon_{kl}\), de orice componentă de tensiune, \(\sigma_{ij}\),adică, \(\sigma_{ij} = C_{ijkl} \epsilon_{kl}\).Legea de transformare a coordonatelor pentru tensorul de rigiditate de rang 4 este ușor de scris în notație tensorială sub forma
\
Ecuația tensorială indică modul de scriere a transformării în notație matricială.
\
Rezumat
Transformarea în coordonate a unui vector în notație matricială și tensorială este
\
Transformarea în coordonate a unui tensor în notație matricială și tensorială este
\
Rețineți că \({\bf Q}\) și \(\lambda_{ij}\) sunt aceeași matrice de transformare.
În 2-D, \({\bf Q}\) și \(\lambda_{ij}\) sunt definite ca
\\\\]
care este un caz special al formei mai generale 3-D
\\\\\]
.