
Las redes neuronales y las matemáticas son inseparables y eso es probablemente lo que asusta a la mayoría de la gente. He oído demasiados comentarios dudosos sobre el aprendizaje profundo, «Oh, esto es demasiado matemático para que yo lo comprenda», «¿Cuántas empresas están utilizando realmente el aprendizaje profundo? Prefiero ahorrarme el trabajo mental y mantenerme alejado de estos conceptos tan exigentes».
Pero si lo piensas, no es tan difícil. Créeme. Para entender por qué un algoritmo se comporta de una determinada manera, es esencial comprender lo que ocurre entre bastidores. Los complejos algoritmos de aprendizaje automático están empaquetados convenientemente para nosotros hoy en día y están a sólo una llamada de función. Las derivadas de las funciones de activación son conceptos algo menos obvios que a menudo tendemos a ignorar. Sin embargo, forman la base de poderosos algoritmos y poner un poco de esfuerzo extra para entenderlos ciertamente vale la pena. Después de leer este artículo estará un paso más cerca de desentrañar lo que se esconde bajo la fachada de la «caja negra».
Antecedentes
Las redes neuronales utilizan una variedad de funciones de activación en las capas ocultas y de salida para catalizar el proceso de aprendizaje. Algunas de las funciones de activación más utilizadas son las funciones Sigmoid y tanH. La función de activación más popular es la ReLU (Unidad Lineal Rectificada) debido a su capacidad para superar eficazmente el problema del gradiente de fuga. Una visión profunda de las funciones de activación es para otro día. Hoy nos centraremos en las matemáticas que hay detrás de la derivada de la función sigmoide.
¿Por qué es importante la derivada de una función de activación?
Como probablemente sepas, las redes neuronales se mueven en dos pasos:
- Propagación hacia delante – Los datos de entrada fluyen a través de la red y obtenemos la salida predicha. La comparamos con la salida real y calculamos el error.
- Propagación hacia atrás – El error calculado se utiliza para actualizar los parámetros de la red neuronal utilizando la derivada de la función de activación.
La función sigmoidea
La función sigmoidea, caracterizada por una curva en forma de S, se suele denominar un caso especial de la función logística. Es más útil en los casos en los que tenemos que predecir la probabilidad como salida.
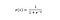
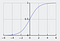
La función sigmoidea arroja valores que se encuentran entre 0 y 1 (con razón si se tiene en cuenta que predice probabilidades).
La derivada sigmoidea
Este bloque de construcción fundamental que ayuda a entrenar las redes neuronales tiene la forma:


Sin más preámbulos, ¡vamos a poner en marcha la derivación!
Aproximación 1

Aproximación 2:
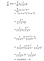
¿Por qué utilizamos esta versión de la derivada?
En el paso de propagación hacia delante, se calcula la función sigmoide (σ(x)) y se tiene su valor a mano. Mientras que el cálculo de la derivada en el paso de retropropagación, todo lo que tienes que hacer es conectar el valor de σ(x) en la fórmula derivada anteriormente y voila, usted es bueno para ir!
Eso es todo chicos! Gracias por leer!