AC, eller växelström, kallas så eftersom strömmen växlar mellan två polariteter. Med andra ord är strömmen (och följaktligen spänningen) en funktion av tiden. Detta skiljer sig fundamentalt från likström som är fast i polaritet och i allmänhet konstant över tiden. En likspänningskälla i ett laboratorium, till exempel, håller idealt sett en fast spänning över sina terminaler och varierar inte över tiden. När en växelströmsvågform däremot svänger fram och tillbaka genom tiden kan dess form uppvisa stora variationer som sträcker sig från de enkla, regelbundna banorna i laboratoriestandarder som sinusvågor, triangelvågor och fyrkantsvågor, till de mycket mer komplexa och böljande vågformer som produceras av musikinstrument och den mänskliga rösten.
Sinusvågen är den enklaste våg som kan skapas. Den representerar rörelsen hos en enkel vektor som roterar med konstant hastighet, t.ex. den vertikala förskjutningen av sekundvisaren på en klocka. Ett exempel visas i figur \(\PageIndex{1}\). Den horisontella axeln visar tiden. Den ökar när vi rör oss från vänster till höger (dvs. om punkt A ligger till höger om punkt B så inträffar A senare i tiden än B). Den vertikala axeln representeras här i allmänhet som en procentsats av maximalt värde, men skulle vanligtvis vara ett mått på spänning, ström, ljudtryck eller liknande.
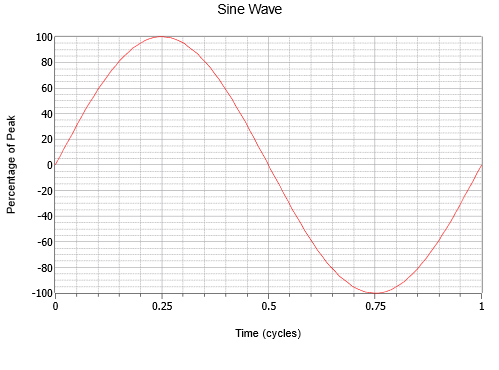
Figur \(\PageIndex{1}\): En sinusvåg.
Notera den jämna variationen som börjar vid noll, stiger till en positiv topp en fjärdedel av vägen, faller tillbaka till noll efter halva vägen, fortsätter till en negativ topp tre fjärdedelar av vägen och stiger sedan igen till där den började. Denna process upprepas sedan. Varje upprepning kallas för en cykel. I figur \(\PageIndex{1}\) visas en fullständig cykel.
Sinusvågor uppvisar kvartsvågsymmetri. Det vill säga, varje fjärdedel (i tid) av vågen är identisk med alla andra om man helt enkelt vänder den runt den horisontella axeln och/eller roterar den upprätt runt sin topp. Den tid det tar att slutföra en cykel kallas period och betecknas med symbolen \(T\) (för tid). Periodens reciprok är frekvensen, \(f\).
\
Frekvensen anger hur många cykler som finns på en sekund. För att hedra en av 1800-talets forskare på området använder vi i stället för att kalla enheten ”cykler per sekund” Hertz, uppkallat efter Heinrich Hertz och förkortat Hz. I figur \(\PageIndex{2}\) visas tre sinusvågor med olika frekvenser; den ursprungliga vågen (grön), en våg med dubbla frekvensen (blå) och en tredje med halva frekvensen eller dubbla perioden (röd).
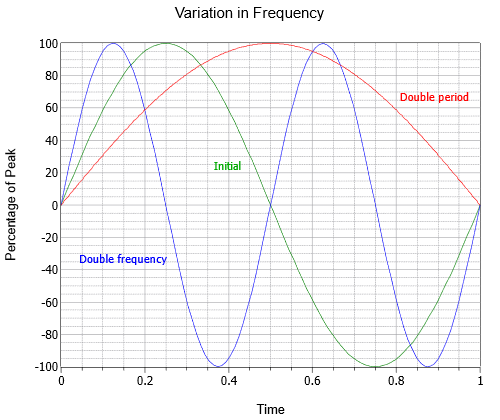
Figur \(\PageIndex{2}\): Sinusvågens frekvensvariation.
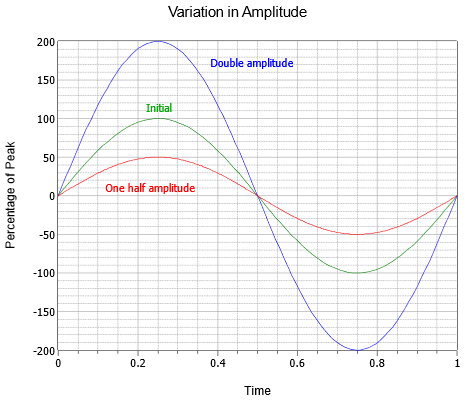
Vågens amplitud (vertikal) kan uttryckas som en toppmängd, som är förändringen från den centrala nollinjen upp till det mest positiva värdet. Amplituden kan också uttryckas som peak-to-peak; avståndet från det mest negativa till det mest positiva värdet. För en sinusvåg kommer detta alltid att vara dubbelt så stort som toppvärdet, även om detta kanske inte är fallet för andra vågor som kan vara asymmetriska. En serie av tre sinusvågor med olika amplituder visas i figur \(\PageIndex{3}\). Vid sidan av den ursprungliga (grön) finns versioner med dubbel amplitud (blå) och halv amplitud (röd).
Figur \(\PageIndex{3}\): Om man kombinerar dessa parametrar kan man betrakta den spänningsvågform som visas i figur \(\PageIndex{4}\). Här ser vi två cykler av en växelspänningsvågform.
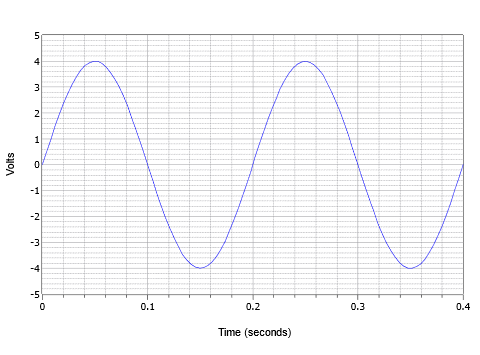
Figur \(\PageIndex{4}\): Grundläggande exempel på en sinusvåg.
Toppvärdet är 4 volt och topp-till-toppvärdet är 8 volt (vanligtvis förkortat som ”8 V pp”). Perioden för en cykel är 0,2 sekunder eller \(T = 200\) millisekunder. Vidare är frekvensen \(f = 1/200\) millisekunder, eller 5 Hz (5 cykler på en sekund).
Ac-vågformer kan också kombineras med en likströmsförskjutning. Genom att lägga till en positiv likströmsnivå förskjuts vågen vertikalt uppåt, medan en negativ likströmsnivå förskjuter vågen vertikalt nedåt. Detta ändrar inte frekvensen eller växelströmsdelen av amplituden (även om de absoluta topparna skulle förskjutas med likströmsvärdet). Figur \(\PageIndex{5}\) visar effekten av olika DC-förskjutningar. Ovanför den ursprungliga vågen (grön) finns en i övrigt identisk våg med en positiv DC-förskjutning som motsvarar 20 % av det ursprungliga toppvärdet (blå). Under den ursprungliga vågen finns en tredje våg (röd) som uppvisar en negativ DC-förskjutning som motsvarar hälften av det ursprungliga toppvärdet.
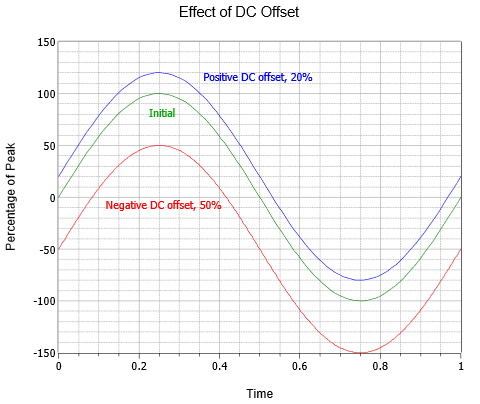
Figur \(\PageIndex{5}\): Det är dessutom möjligt att en sinusvåg är förskjuten i tid jämfört med en annan sinusvåg eller en referens. Även om det är möjligt att ange denna förskjutning som en absolut tid, är det vanligare att göra det som en fasförskjutning, det vill säga tiden uttryckt som en del av perioden i grader. Om t.ex. en sinus ligger en fjärdedel av perioden före en annan sägs den ligga 90\(^{\circ}\) före (dvs. 1/4 av 360\(^{\circ}\)). Om den ligger efter med ½ av perioden sägs den ligga efter med 180\(^{\circ}\) (dvs. en 1/2 cykel senare i tiden). Ett annat sätt att uttrycka detta är att ledande vågformer börjar tidigare i tiden och ritas därför till vänster om referensen, medan eftersläpande vågformer börjar senare i tiden och ritas till höger.
Figur \(\PageIndex{6}\) illustrerar effekten av fasförskjutning. Observera att \(t = 0\) har flyttats till mitten av den horisontella axeln. Den mellersta kurvan är den ursprungliga eller referensvågen (grön). Till vänster (röd) är en våg som leder den inledande vågen med en åttondels cykel, eller 45\(^{\circ}\). Till höger (blått) finns en halvt så lång efterföljande våg, eller -22,5\(^{\circ}\).
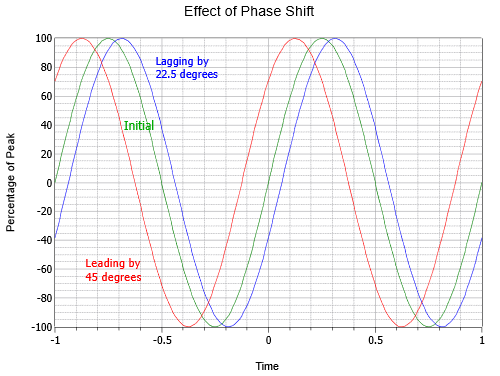
Figur \(\PageIndex{6}\): Sinusvågens fasvariation.
Med hjälp av kombinationen av ovanstående element kan vi utveckla ett allmänt format för en sinusvåg (spänning visas):
\
Varvid
\(v(t)\) är spänningen vid en viss tidpunkt \(t\),
\(V_{DC}\) är den eventuella likströmsförskjutningen,
\(V_{P}\) är toppvärdet,
\(f\) är frekvensen,
\(\theta\) är fasförskjutningen (+ om den är ledande och ritad till vänster, – om den är eftersatt och ritad till höger).
För ett snabbt och praktiskt exempel har den vågform som visas i figur \(\PageIndex{4}\) en amplitud på 4 volts toppvärde, en frekvens på 5 Hz och ingen DC-förskjutning eller fasförskjutning. Därför är dess uttryck \(v(t) = 4 \sin (2 \pi 5 t)\)
För att beräkna en fasförskjutning ska du först bestämma tidsdifferensen mellan vågformen och referensen, som vi kallar \(\Delta t\). Referensen kan vara en fast punkt i tiden (t.ex. \(t = 0\)) eller en annan vågform. I allmänhet är det enkla sättet att göra detta att mäta skillnaden vid nollgenomgångarna, förutsatt att det inte finns någon DC-förskjutning. Om det finns en förskjutning, gör mätningen där nollgenomgången har förskjutits till (dvs. vid DC-förskjutningsnivån). När skillnaden har hittats dividerar du den med perioden för att representera förskjutningen som en bråkdel av en period. Eftersom en cykel motsvarar en rotation av vektorn, eller 360 grader, multipliceras bråket helt enkelt med 360 grader för att hitta fasförskjutningen i grader. Uttryckt som en formel:
\
Håll i minnet att om vågen är förskjuten till vänster är den ledande och positiv, medan en förskjutning till höger är eftersläpande eller fördröjd i tiden, och därmed negativ.
Exempel \(\PageIndex{1}\)
Skriv uttrycket för den vågform som visas i figur \(\PageIndex{7}\).
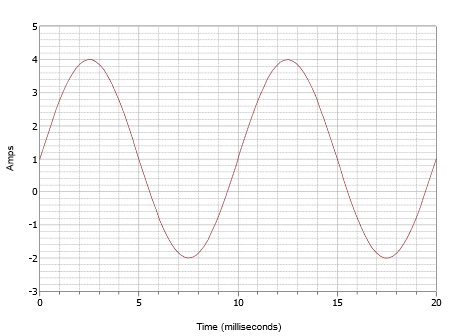
Figur \(\PageIndex{7}\): Vågform för exempel \(\(\PageIndex{1}\).
Denna vågform kan ytligt sett se ut som den i figur \(\(\PageIndex{4}\) men låt dig inte luras. För det första är tidsskalan annorlunda. För den här vågformen slutar en cykel på 10 millisekunder. Därför är frekvensen
\
\
\
Det andra problemet är DC-förskjutningen. Observera att den positiva toppen uppstår vid 4 ampere medan den negativa toppen uppstår vid -2 ampere. Detta indikerar ett topp-toppvärde på 6 ampere. Utan en förskjutning skulle den positiva toppen vara vid 3 ampere, därför finns det en +1 ampere DC-förskjutning. Vågformens vertikala centrum förskjuts uppåt från 0 ampere till +1 ampere. Denna punkt är vid t = 0, därför finns det ingen fasförskjutning. Det resulterande uttrycket är:
\
Exempel \(\PageIndex{2}\)
Skriv uttrycket för den vågform som visas i figur \(\PageIndex{8}\).
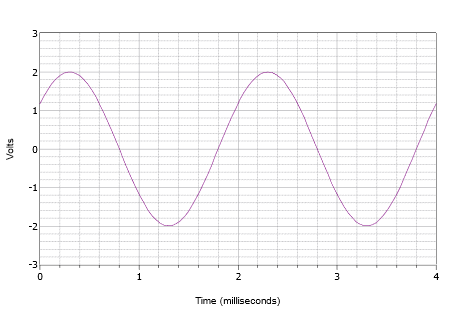
Figur \(\PageIndex{8}\): Vågform för exempel \(\PageIndex{2}\).
För det första är den positiva toppen 2 volt och topp-till-topp-värdet är 4 volt. Därför finns det ingen likströmsförskjutning. Vågens vertikala centrum börjar inte vid \(t = 0\), så det måste finnas en fasförskjutning. Värdet vid \(t = 0\) är 1,2 volt. Vågen når samma amplitud vid \(t = 2\) millisekunder och börjar upprepa ytterligare en cykel. Följaktligen måste perioden vara 2 millisekunder. Frekvensen är reciproken av detta värde, alltså \(f = 500\) Hz.
Vågformen är förskjuten till vänster vilket indikerar en positiv eller ledande fasförskjutning. Om vi undersöker den andra cykeln ser vi att den når noll volt vid 1,8 millisekunder. Därför är förskjutningen 0,2 millisekunder. Uttryckt i grader är detta:
\
\
\
Det slutliga uttrycket är:
\
Exempel \(\PageIndex{3}\)
Rita upp den vågform som motsvarar följande uttryck.
\
Först noterar du att förskjutningen på -3 volt trycker ner den positiva toppen från 5 volt till 2 volt och den negativa toppen från -5 volt till -8 volt. Frekvensen 40 kHz dikterar en period på:
\
\
\
Fasförskjutningen på -72\(^{\circ}\) motsvarar 72/360, eller 0,2 cykler. Detta motsvarar en tidsfördröjning (förskjuten till höger eftersom den är negativ) på 0,2 gånger 25 \(\mu\)s, eller 5 \(\mu\)s.
Inledningsvis är det ofta bäst att konstruera plottet via en serie diskreta steg i stället för att försöka rita upp det hela i ett svep. Rita först en sinusvåg med en toppamplitud på 5 volt och en period på 25 \(\mu\)s. Tryck nu ner vågformen med 3 volt så att den positiva toppen är endast 2 volt och den negativa toppen är nere på -8 volt. Slutligen, tryck den nyligen förskjutna vågformen till höger med 5 \(\mu\)s. Resultatet visas i figur \(\PageIndex{9}\).
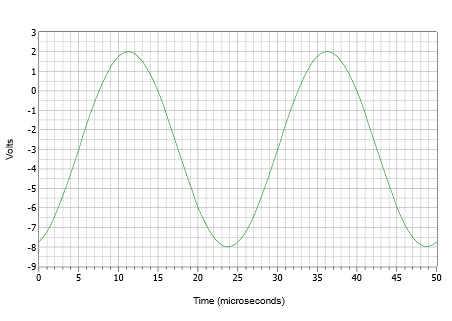
Figur \(\PageIndex{9}\): Vågform för exempel \(\PageIndex{3}\).
1.2.1: Laboratoriemätningar
I laboratoriet används en funktionsgenerator för att generera sinusformer och andra vågformer. Dessa anordningar gör det möjligt att exakt kontrollera både vågens amplitud och frekvens tillsammans med att lägga till en likströmsförskjutning, om så önskas. Ett exempel visas i figur \(\PageIndex{10}\). Det motsvarande mätverktyget är oscilloskopet, eller kort och gott scope.

Figur \(\PageIndex{10}\): Laboratoriets signalgenerator.
Oscilloskopet är kanske det mest användbara och mångsidiga mätinstrumentet i laboratoriet. Vanligtvis har de antingen två eller fyra ingångskanaler, även om fler är möjliga. Varje ingångskanal har sin egen känslighetsjustering och alla kanaler har en gemensam tidsreferens. På displayen visas vågformer på samma sätt som i figurerna \(\PageIndex{1}\) – \(\PageIndex{9}\). De kan också plotta en spänning mot en annan (X – Y-läge). Moderna oscilloskop har ytterligare funktioner som automatisk mätning av frekvens, amplitud, fasförskjutning etc., markörbaserade mätningar och möjlighet att spara visningsbilder som grafikfiler. Ett exempel på ett digitalt oscilloskop med fyra kanaler visas i figur \(\PageIndex{11}\).

Figur \(\PageIndex{11}\): Ett digitalt oscilloskop.
1.2.2.2: Schematiska symboler
Som schematiska symboler visas symbolerna för växelspännings- och strömkällor i figur \(\PageIndex{12}\). Polaritets- och riktningsmarkeringarna är inte absoluta; det rör sig trots allt om växelströmskällor vars polaritet och riktningar vänds fram och tillbaka. Markeringarna används istället för att fastställa en tidsreferens, särskilt i kretsar som använder flera källor.
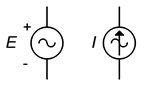
Figur \(\PageIndex{12}\): Schematiska symboler för en växelspänningskälla (vänster) och en strömkälla (höger).
Det är värt att komma ihåg att negera en källa är detsamma som att vända på dess polaritet. Detta gällde för likströmskällor och gäller fortfarande för växelströmskällor. Detta illustreras i figur \(\PageIndex{13}\). Ibland gör det att vända eller negera en källa analysen lite tydligare eller lättare att visualisera.
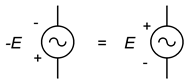
Figur \(\PageIndex{13}\):
Exempel \(\PageIndex{4}\)
Antag att ett oscilloskop visar två vågor enligt figur \(\PageIndex{14}\). Bestäm fasförskjutningen av den mindre vågformen med 20 volts topp (blå) i förhållande till den större vågformen med 25 volts topp (röd).
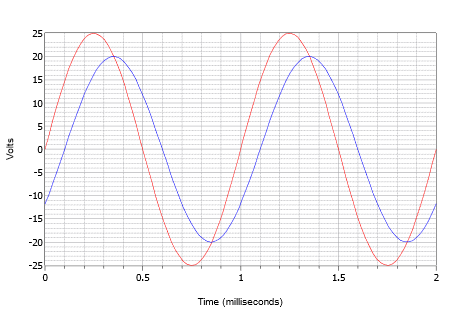
Figur \(\PageIndex{14}\): Vågformer för exempel \(\PageIndex{4}\).
Först noterar man att ingen av vågen uppvisar en likströmsförskjutning. Om en eller båda hade en förskjutning skulle vågen/vågarna behöva förskjutas vertikalt så att deras normala nollgenomgångspunkter skulle ligga på samma nivå. Vid mätning av båda vågorna finner man att perioden är 1 millisekund. Tidsförskjutningen kan lättast hittas vid någon av nollpunkterna (det finns fyra platser att välja mellan). Fördröjningen är en liten avvikelse, eller 0,1 millisekund, där den mindre vågen är fördröjd i tid, eller släpar efter den större vågen. Detta indikerar en negativ fasförskjutning.
\
\
\
1.2.3: Sina och cosinus
Det finns en handfull specifika fasförskjutningar som är värda att titta närmare på. Om en sinusvåg är inverterad, det vill säga vänd upp och ner, går det inte att skilja den från en sinusvåg som har förskjutits antingen +180 eller -180 grader. Med andra ord kan en sådan våg skrivas på tre olika sätt: Det kan alltså beskrivas på tre olika sätt: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\), eller \(\sin (2 \pi ft + 180^{\circ})\). Om en sinusvåg är förskjuten med +90 grader (dvs. framåt och åt vänster) kan den också kallas för en cosinusvåg. Således \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Slutligen, om en sinusvåg förskjuts med -90 grader (dvs. eftersläpande och till höger) kan den kallas en negativ eller inverterad cosinusvåg. Således \(\sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). Förhållandet mellan dessa fyra vågor illustreras i figur \(\PageIndex{15}\).
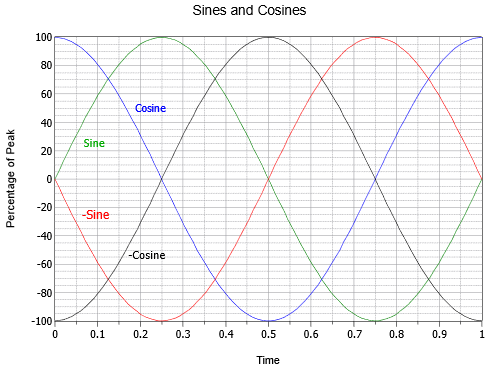
Figur \(\PageIndex{15}\): Tidsförhållanden mellan sinus och cosinus.
Det är också värt att notera att cosinusvågen representerar den första derivatan, eller lutningen, av sinusvågen. Som du kanske minns från andra studier är en linjes lutning eller ”branthet” förhållandet mellan den vertikala förändringen och den horisontella förändringen, vilket ibland kallas ”stigningen över löpningen”. För en spänning skulle det vara förändringen i spänning i förhållande till förändringen i tid, eller \(\Delta V/ \Delta t\). För en jämn, kontinuerligt föränderlig kurva som en sinusvåg definieras lutningen vid en given punkt korrekt som den första derivatan, eller \(dv/dt\) i det här fallet. För att visuellt verifiera att detta stämmer, observera att den brantaste delen av sinusvågen (grön) är där den passerar nollamplituden. När den passerar noll samtidigt som den rör sig positivt (vid \(t = 0\) eller \(t = 1\) i figur \(\(\PageIndex{15}\)) är cosinus (blå) vid sin positiva topp. När sinus passerar noll vid en negativ rörelse (vid \(t = 0,5\)) har cosinus sin negativa topp. Vidare är sinusvågen platt med en lutning på noll vid sina positiva och negativa toppar (vid \(t = 0,25\) respektive \(t = 0,75\)), och vid dessa tidpunkter är cosinusens amplitud också noll. Det är också sant att sinusvågen är lutningen av den negativa cosinusvågen, att den negativa cosinusvågen är lutningen av den negativa sinusvågen och att den negativa sinusvågen är lutningen av cosinusvågen. Om vi går i motsatt riktning kan vi säga att antiderivatan (obestämd integral) av en cosinusvåg är en sinusvåg, integralen av en sinusvåg är en negativ cosinusvåg och så vidare. Dessa relationer kommer att visa sig vara mest användbara när vi vänder oss till kondensatorers och induktorers respons i växelströmskretsar.
1.2.4: RMS – Root Mean Square Measurement
Samman med peak och peak-to-peak kan amplitud anges som ett RMS-värde (Root Mean Square). Om peak eller peak-to-peak inte anges antas mätningen vara RMS. RMS är en speciell beräkning som används för att hitta ekvivalent likströmseffekt (mycket vanligt, till exempel med ljudförstärkare). Med andra ord, om vi är intresserade av att hitta effekten i ett motstånd måste beräkningen utföras med hjälp av RMS-värden för spänning eller ström, inte topp- eller topp-till-topp-värden. Om man inte gör det kommer man att få felaktiga effekter. Detta gäller oavsett vågform; vare sig det är en sinusvåg, triangelvåg eller komplexa vågor i musiksignaler. Om en spänning anges som RMS kan den behandlas för effektberäkningar precis som en likvärdig likspänning. Exempelvis kommer en sinusspänning på 1 volt RMS att ge upphov till samma effektförlust och uppvärmning i ett givet motstånd som en likspänning på 1 volt. Av denna anledning kallas RMS ibland för det effektiva värdet (dvs. effektivt likströmsvärde).
Namnet root-mean-square beskriver processen för att bestämma det effektiva värdet. Minns först att effekten är proportionell mot kvadraten på spänningen eller strömmen. Vårt första steg blir alltså att kvadrera den ingående vågformen. Naturligtvis är vågformen en funktion av tiden och dess kvadrat kommer att ge en ny form. Nu måste vi hitta medelvärdet för denna nya form. Anledningen till detta är enkel, men inte nödvändigtvis uppenbar. Elektriska och elektroniska komponenter har massa och värms eller kyls därför inte omedelbart. De uppvisar en termisk tidskonstant. Därför reagerar de på den genomsnittliga inmatningen över tiden. Även om vi skulle kunna beräkna någon form av ”momentan toppeffekt” vid ett visst ögonblick i tiden, representerar detta inte den likvärdiga likströmseffekten. När vi väl har fått fram medelvärdet av denna kvadrerade vågform är motsvarande likströmsvärde bara kvadratroten av medelvärdet. Resultatet är ett bråkvärde mellan noll och ett som används som en skalfaktor för att omvandla ett toppvärde till ett RMS-värde. Värdet kommer att vara unikt för den specifika vågformen. Det vill säga, alla sinusvågor (oavsett fas) har samma faktor, alla regelbundna triangelvågor har samma faktor och så vidare. Eftersom vi främst ägnar oss åt sinuskurvor, ska vi titta närmare på hur vi bestämmer RMS-faktorn för dem.
Vi börjar med det grundläggande uttrycket för en sinusvåg utan DC-förskjutning eller fasförskjutning, och med en amplitud på ett:
\
Det första steget är att kvadrera denna vågform. En användbar trigonometrisk identitet är
\
Om man tillämpar detta på vår våg får man:
\
Detta uttryck beskriver en inverterad cosinusvåg med dubbla den ursprungliga frekvensen och halva den ursprungliga amplituden, som rider på en likströmsförskjutning som är lika med dess toppvärde. Med andra ord är den negativa toppen av cosinusvinkeln vid noll och den positiva toppen vid 1. Nästa steg är att hitta medelvärdet eller medelvärdet av detta mellanresultat. Medelvärdet är lika med förskjutningen på 0,5. Detta kan åskådliggöras som att området ovanför förskjutningen fyller perfekt ”dippen” under förskjutningen. Det sista steget är att ta kvadratroten av medelvärdet. Kvadratroten av 0,5 är lika med ett över kvadratroten av två, eller ungefär 0,707. Därför är RMS-värdet 0,707 gånger toppvärdet. Alternativt kan du dividera toppvärdet med kvadratroten av två, dvs. ungefär 1,414. Denna process visas grafiskt i figur \(\PageIndex{16}\).
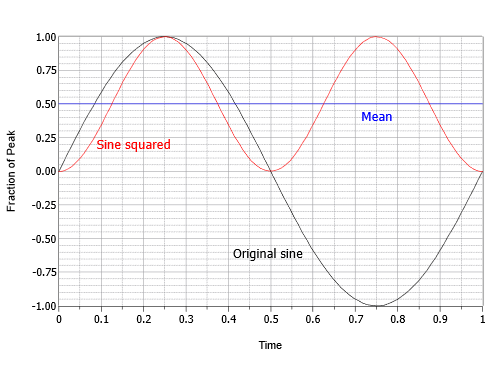
Figur \(\PageIndex{16}\): Process för att hitta RMS-faktorn för sinusvågor.
För sinusvågor är RMS alltid toppvärdet gånger 0,707. Vi kan också säga att RMS-värdet för en sinusvåg är dess toppvärde dividerat med ungefär 1,414. Återigen skulle dessa förhållanden inte nödvändigtvis gälla för icke-sinusvågor. Detaljer om andra vanliga former finns i tillägg C. Slutligen kallas förhållandet mellan toppvärdet och RMS-värdet för toppförhållandet. Detta är ett fast värde för sinusvågor (återigen ca 1,414), men kan vara över 10:1 för vissa typer av ljudsignaler.
1.2.5: Våglängd
En annan sak av intresse är vågens utbredningshastighet. Denna varierar kraftigt. I fallet med ljus i ett vakuum (eller till en nära approximation en elektrisk ström i en tråd) är hastigheten cirka 3E8 meter per sekund (dvs. 300 000 km/s) eller cirka 186 000 miles per sekund.
Givet en hastighet och en period kan vi föreställa oss hur långt ifrån varandra vågens toppar är. Detta avstånd kallas våglängden och betecknas med den grekiska bokstaven lambda \(\lambda\). Våglängden är lika med hastigheten dividerad med frekvensen, \(\lambda = v/f\). För en högtalare som producerar en 100 Hz sinus, eftersom ljudets hastighet i luft är 344 m/s, blir \(\lambda = 344 m/s \, / \, 100\) Hz, eller 3,44 meter (lite mer än 11 fot). Observera att ju högre frekvens desto kortare våglängd. Observera också att ju snabbare hastigheten är, desto längre är våglängden. Beräkningar av våglängder är särskilt viktiga inom telekommunikation och akustik.