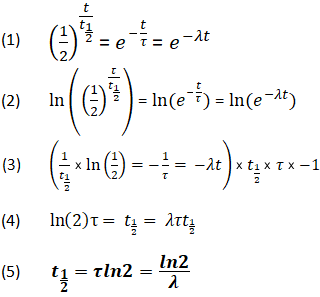Med följande verktyg kan du generera något av värdena från de tre andra i formeln för halveringstid för att ett ämne som genomgår sönderfall ska minska med hälften.

Halveringstidskalkylator
Ange tre av följande värden för att beräkna det fjärde värdet.
Omräkning av halveringstid, medellivslängd och sönderfallskonstant
Ange något av följande för att få fram de andra två.
Definition och formel
Halveringstid definieras som den tid som det tar för en given mängd att minska till hälften av sitt ursprungliga värde. Termen används oftast i samband med atomer som genomgår radioaktivt sönderfall, men kan användas för att beskriva andra typer av sönderfall, oavsett om det är exponentiellt eller inte. En av de mest kända tillämpningarna av halveringstid är kol-14-datering. Halveringstiden för kol-14 är cirka 5 730 år, och det kan användas på ett tillförlitligt sätt för att mäta datum upp till cirka 50 000 år sedan. Processen för kol-14-datering utvecklades av William Libby och bygger på det faktum att kol-14 ständigt bildas i atmosfären. Det införlivas i växter genom fotosyntesen och sedan i djur när de äter växter. Kol-14 genomgår ett radioaktivt sönderfall när växten eller djuret dör, och genom att mäta mängden kol-14 i ett prov får man information om när växten eller djuret dog.
Nedan visas tre likvärdiga formler som beskriver exponentiellt sönderfall:
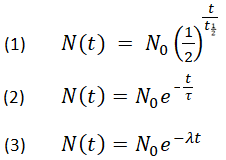
- där
N0 är den ursprungliga kvantiteten
Nt är den kvarvarande kvantiteten efter tid, t
t1/2 är halveringstiden
τ är medellivslängden
λ är sönderfallskonstanten
Om en arkeolog hittade ett fossilt prov som innehöll 25 % kol-14 i jämförelse med ett levande prov, skulle tiden för det fossila provets död kunna bestämmas genom att omorganisera ekvation 1, eftersom Nt, N0 och t1/2 är kända.
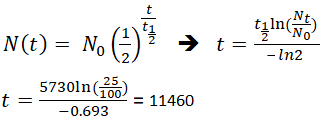
Detta innebär att fossilet är 11 460 år gammalt.
Avledning av förhållandet mellan halveringstidskonstanter
Med hjälp av ekvationerna ovan är det också möjligt att härleda ett förhållande mellan t1/2, τ och λ. Detta förhållande gör det möjligt att bestämma alla värden, så länge som minst ett är känt.