Hur man tänker med exponenter och logaritmer

Här är ett knep för att lösa problem med exponenter och logaritmer. Ställ bara två frågor:

1) Talar vi om inputs (orsaken till förändringen) eller outputs (den faktiska förändringen som skedde?)

Logaritmer avslöjar de inputs som orsakade tillväxten
Exponenterna hittar det slutgiltiga resultatet av tillväxten

2) Talar vi om odlarens perspektiv, eller en observatörs?

e och den naturliga loggen är från odlarens ögonblick-för-ögonblick-perspektiv
Bas 10, bas 2 osv. är mått som är bekväma för en mänsklig observatör

I mitt huvud placerar jag alternativen i en tabell:

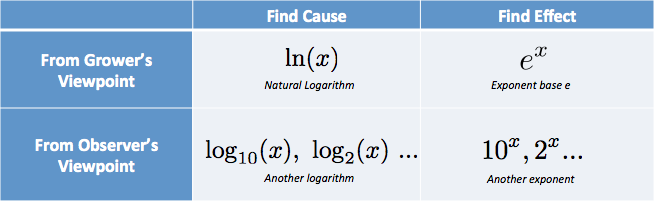
exponent logaritm synpunktsjämförelse

Jag har tankar som ”Jag behöver orsaken, från odlarens perspektiv… det är den naturliga loggen.”. (Natural log förkortas med LN med små bokstäver, från det högtravande logaritmus naturalis.)

Jag var frustrerad över lektioner som beskrev tabellens inre del, de råa funktionerna, utan bildtexter som förklarade när man skulle använda dem!

Det går inte, låt oss få direkt övning i att tänka med logaritmer och exponenter.

Scenario: Här är ett typiskt exempel på tillväxt:

Från 2000 till 2010 ändrades USA:s BNP från 9,9 biljoner till 14,4 biljoner

Okej, visst, de siffrorna visar att det har skett en förändring. Men vi vill förmodligen ha en inblick i orsaken: Vilken genomsnittlig årlig tillväxttakt skulle förklara denna förändring?

Omedelbart tänker min hjärna ”logaritmer” eftersom vi arbetar bakåt från tillväxten till den takt som orsakade den. Jag börjar med en tanke som denna:

$\displaystyle{\text{logaritm av förändring} \rightarrow \text{orsak till tillväxten} }$

En bra början, men låt oss skärpa den.

Först, vilken logaritm ska vi använda?

Som standard väljer jag den naturliga logaritmen. De flesta händelser hamnar i termer av odlaren (inte observatören), och jag gillar att ”åka med” med det växande elementet för att visualisera vad som händer. (Radianer är liknande: de mäter vinklar i termer av den som rör sig.)

Nästa fråga: vilken förändring tillämpar vi logaritmen på?

Vi är egentligen bara intresserade av förhållandet mellan början och slut: 9,9 biljoner till 14,4 biljoner på 10 år. Detta är samma tillväxttakt som att gå från \$9,90 till \$14,40 under samma period.

Vi kan skärpa vår tanke:

$\displaystyle{\text{naturlig logaritm av tillväxtkvoten} \rightarrow \text{orsak till tillväxt} }$

$\displaystyle{\ln(\frac{14.4}{9.9}) = .374}$

Ok, orsaken var en tillväxtkvot på .374 eller 37,4%. Är vi klara?

Inte ännu. Logaritmer vet inte om hur lång tid en förändring tog (vi har inte satt in 10 år, eller hur?). De ger oss en hastighet som om hela förändringen skedde under en enda tidsperiod.

Förändringen kan faktiskt vara ett enda år med 37,4 % kontinuerlig tillväxt, eller två år med 18,7 % tillväxt, eller någon annan kombination.

Från scenariot vet vi att förändringen tog 10 år, så hastigheten måste ha varit:

$\displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3,74\%}$

Från synvinkeln av omedelbar, kontinuerlig tillväxt växte USA:s ekonomi med 3,74% per år.

Är vi klara nu? Inte riktigt!

Denna kontinuerliga takt är ur tillväxtens perspektiv, som om vi ”åker med” med ekonomin när den förändras. En bankman bryr sig förmodligen om den människovänliga skillnaden från år till år. Vi kan räkna ut detta genom att låta den kontinuerliga tillväxten löpa under ett år:

$\displaystyle{\text{exponent med kurs och tid} \rightarrow \text{effekt av tillväxt} }$

$\displaystyle{e^{\text{rate} \cdot \text{tid}} = \text{tillväxt}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

Den årliga vinsten är 3,8 %, vilket är något högre än den momentana räntan på 3,74 % på grund av sammansättningen. Här är ett annat sätt att uttrycka det:

Från en instant-by-instant basis växer en given del av ekonomin med 3,74%, modellerat med $e^(.0374 * år)$
På årsbasis, med sammansättningseffekter räknade, växer ekonomin med 3,81 %, modellerat med $1.0381^år$

Inom ekonomi vill vi kanske ha förändringen från år till år, som kan jämföras fint med andra trender. Inom vetenskap och teknik föredrar vi att modellera beteende på ögonblicklig basis.

Scenario: Beskriv naturlig tillväxt

Jag avskyr konstruerade exempel som ”Anta att en bakterie fördubblas varje 24 timmar, hitta dess tillväxtformel”. Replikerar sig bakteriekolonier med rena mänskliga intervaller, och väntar vi på en exakt fördubbling?

Ett bättre scenario: ”Hej, jag hittade några bakterier, väntade en timme, och klumpen växte från 2,3 gram till 2,32 gram. Jag går till lunch nu. Räkna ut hur mycket vi kommer att ha när jag är tillbaka om tre timmar.”

Låt oss modellera detta. Vi behöver en logaritm för att hitta tillväxttakten och sedan en exponent för att projicera denna tillväxt framåt. Liksom tidigare, låt oss hålla allt i termer av den naturliga logaritmen till att börja med.

Växtfaktorn är:

$\displaystyle{\text{logaritm av förändring} \rightarrow \text{orsak till tillväxt} }$

$\displaystyle{\ln(\text{tillväxt}) = \ln(2.32/2.3) = .0086 = .86\%}$

Detta är hastigheten för en timme, och den generella modellen för att projicera framåt blir

$\displaystyle{\text{exponent med hastighet och tid} \rightarrow \text{effekt av tillväxt} }$

$\displaystyle{e^{.0086 \cdot \text{timmar}} \rightarrow \text{effekt av tillväxt} }$

Om vi börjar med 2,32 och växer i 3 timmar får vi:

$\displaystyle{2,32 \cdot e^{.0086 \cdot 3} = 2,38}$

För skojs skull, hur lång tid tar det innan bakterien fördubblas? Tänk dig att vänta på att 1 ska bli 2:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hours}}} = 2}$

Vi kan mekaniskt ta det naturliga logaritmet av båda sidor för att ”upphäva exponenten”, men låt oss tänka intuitivt.

Om 2 är slutresultatet är ln(2) tillväxtinsatsen som fick oss dit (viss hastighet × tid). Vi vet att hastigheten var 0,0086, så tiden för att nå 2 skulle vara:

$\displaystyle{ \text{hours} = \frac{\ln(2)}{\text{rate}} = \frac{.693}{.0086} = 80,58}$

Kolonin kommer att fördubblas efter ~80 timmar. (Glad att du inte stannade kvar?)

Vad betyder perspektivbytet egentligen?

Att räkna ut om du vill ha input (orsaken till tillväxten) eller output (resultatet av tillväxten) är ganska okomplicerat. Men hur visualiserar du odlarens perspektiv?

Föreställ dig att vi har små arbetare som bygger det slutliga tillväxtmönstret (se artikeln om exponenter):

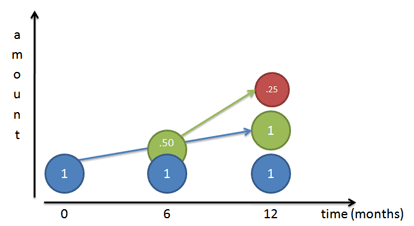
$sammanräknad ränta$

Om vår tillväxthastighet är 100 %, säger vi till vår första arbetare (Mr Blue) att arbeta stadigt och skapa en 100-procentig kopia av sig själv i slutet av året. Om vi följer honom dag för dag ser vi att han faktiskt färdigställer en 100-procentig kopia av sig själv (Mr Green) i slutet av året.

Men… den arbetare som han byggde (Mr Green) börjar också arbeta. Om Mr Green först dyker upp vid 6-månadersgränsen har han ett halvår på sig att arbeta (samma årstakt som Mr Blue) och han bygger Mr Red. Naturligtvis slutar det med att herr Röd är halvfärdig, eftersom herr Grön bara har 6 månader på sig.

Tänk om herr Grön dyker upp efter 4 månader? En månad? En dag? En sekund? Om arbetstagarna börjar växa omedelbart får vi den omedelbara-till-instant-kurvan som definieras av $e^x$:

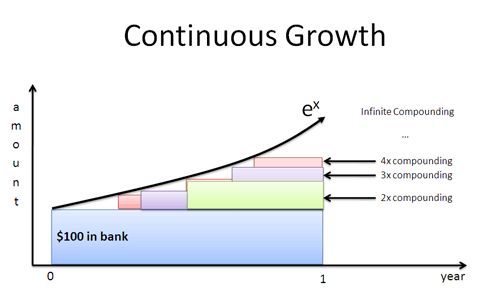
kontinuerlig tillväxt

Den naturliga loggen ger en tillväxttakt i termer av en enskild arbetstagares perspektiv. Vi sätter in denna hastighet i $e^x$ för att hitta slutresultatet, med all sammansättning inkluderad.

Användning av andra baser

Om vi byter till en annan typ av logaritm (bas 10, bas 2 osv.) betyder det att vi letar efter något mönster i den totala tillväxten, inte vad den enskilda arbetstagaren gör.

Varje logaritm ställer en fråga när vi ser en förändring:

Log bas e:
Logbas 2: Hur många fördubblingar krävdes?
Logbas 10: Hur många 10x-ingar krävdes?

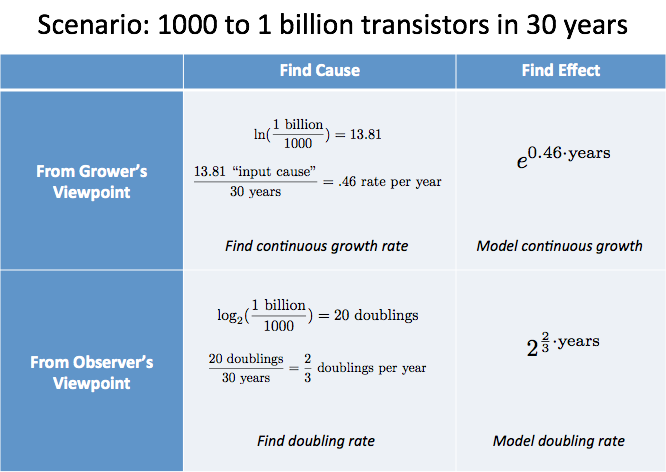
Här är ett scenario att analysera:

Under 30 år har antalet transistorer på typiska chip gått från 1 000 till 1 miljard

Hur skulle du analysera detta?

Mikrochips är inte en enda enhet som växer jämnt över tiden. De är separata utgåvor från konkurrerande företag och visar på en allmän teknisk trend.
Då vi inte ”åker med” på ett växande mikrochip, kan vi använda en skala som är gjord för mänsklig bekvämlighet. Fördubbling är lättare att tänka på än 10x-ing.

Med dessa antaganden får vi:

$\displaystyle{\text{logaritm of change} \rightarrow \text{orsak till tillväxt} }$

$\displaystyle{\log_2(\frac{\text{1 billion}}}{1000}) = \log_2(\text{1 million}) \sim \text{20 fördubblingar}$

”Orsaken till tillväxten” var 20 fördubblingar, som vi vet inträffade under 30 år. Detta motsvarar i genomsnitt 2/3 fördubblingar per år, eller 1,5 år per fördubbling – en trevlig tumregel.

Från odlarens perspektiv skulle vi beräkna $\ln(\text{1 miljard}/1000) / \text{30 år} = 46\%$ kontinuerlig tillväxt (lite svårare att relatera till i detta scenario).

Vi kan sammanfatta vår analys i en tabell:

exponenter transistor exempel

Sammanfattning

Lärande handlar om att hitta de dolda bildtexterna bakom ett begrepp. När används det? Vilken synvinkel tillför det till problemet?

Min nuvarande tolkning är att exponenter ställer frågor om orsak kontra verkan och odlare kontra observatör. Men vi är aldrig klara; en del av det roliga är att se hur vi kan rekapitulera gamla begrepp.

Happy math.

Appendix: Här är hur man kan tänka när man byter baser. Om vi antar en 100 % kontinuerlig tillväxttakt,

ln(x) är tiden för att växa till x

ln(2) är tiden för att växa till 2

Då vi har tiden för att fördubbla kan vi se hur många som skulle ”rymmas” i den totala tiden för att växa till x:

$\displaystyle{\text{Antal fördubblingar från 1 till x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Till exempel, hur många fördubblingar sker från 1 till 64?

Ja, ln(64) = 4,158. Och ln(2) = 0,693. Antalet fördubblingar som passar är:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4.158}{.693} = 6}$

I verkligheten kan miniräknare förlora i precision, så använd om möjligt en direkt log bas 2 funktion. Och naturligtvis kan vi ha ett bråktal: Att gå från 1 till kvadratroten av 2 är ”en halv” fördubbling, eller log2(1,414) = 0,5.

Om vi byter till logbas 10 betyder det att vi räknar antalet 10x-ingar som passar:

$\displaystyle{\text{antal 10x-ingar från 1 till x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Snyggt, eller hur? Läs Användning av logaritmer i den verkliga världen för fler exempel.

Andra inlägg i den här serien

En intuitiv guide till exponentialfunktioner & e
Förståelse av den naturliga logaritmen (ln)
En visuell guide till enkla, sammansatta och kontinuerliga räntesatser
Gemensamma definitioner av e (färgläggning)
Förståelse av exponenter (Varför är 0^0 = 1?)
Användning av logaritmer i den verkliga världen
Hur man tänker med exponenter och logaritmer
Förståelse av diskret vs. kontinuerlig tillväxt
Vad betyder en exponent egentligen?
Q: Varför är e speciellt? (2,718…, inte 2, 3,7 eller ett annat tal?)

Scenario: Här är ett typiskt exempel på tillväxt: Från 2000 till 2010 ändrades USA:s BNP från 9,9 biljoner till 14,4 biljoner