Introduktion
Koordinattransformationer är ointuitiva nog i 2D, och positivt smärtsamma i 3D. På den här sidan behandlas de i följande ordning: (i) vektorer i 2D, (ii) tensorer i 2D, (iii) vektorer i 3D, (iv) tensorer i 3D och slutligen(v) tensortransformationer av fjärde rang.
En viktig aspekt av koordinattransformationer är utvärderingen av transformationsmatrisen, särskilt i 3D. Detta berörs här och diskuteras utförligt på nästa sida.
Det är mycket viktigt att inse att alla koordinattransformationer på denna sida är rotationer av koordinatsystemet medan själva objektet förblir fixerat. ”Objektet” kan vara en vektor, t.ex. kraft eller hastighet, eller en tensor, t.ex. spänning eller töjning i en komponent. Objektrotationer diskuteras i senare avsnitt.
2-D koordinattransformationer av vektorer
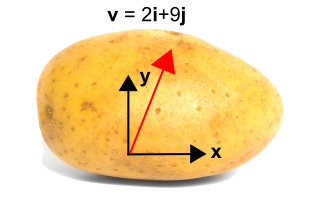
Den akademiska potatisen ger ett utmärkt exempel på hur koordinattransformationer tillämpas på vektorer, samtidigt som den understryker att det är koordinatsystemet som roterar och inte vektorn… eller potatisen.
Potatisen till vänster har en vektor. Men utan ett koordinatsystem finns det inget sätt att beskriva vektorn.Så ett koordinatsystem har lagts till potatisen som visas till höger, vilket gör att vektorn nu kan beskrivas som \({\bf v} = 2{\bf i} + 9{\bf j}\).

Så nu inför vi ett roterat koordinatsystem som visas i blått nedan, där vi använder\(x’\) och \(y’\). Det nya systemet är roterat moturs med en vinkel, \(\theta\),från det ursprungliga koordinatsystemet. Observera att vektorn i sig själv inte förändras alls. Det är fortfarande samma vektor som tidigare. Men den beskrivs med olika numeriska värden i det nya koordinatsystemet. I det här fallet är vektorn närmare parallell med den nya axeln \(x’\) än med axeln \(y’\), så \({\bf i’}\) komponenten kommer att vara större än \({\bf j’}\) komponenten. Transformationen ges under figuren.
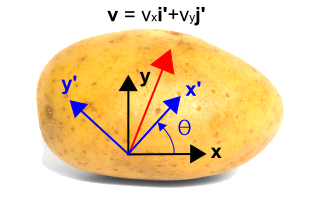
Detta kan ses genom att notera attDessa fyra faktorer utgör de fyra termerna i transformationsekvationerna. De kontrolleras lätt genom att ställa in \(\theta = 0^\circ \) och \(\theta = 90^\circ \). När \(\theta = 0^\circ\), då \(v’_x = v_x\) och \(v’_y = v_y\). När \(\theta = 90^\circ\), då \(v’_x = v_y\) och \(v’_y = -v_x\).
Transformationsmatris
Det är bekvämare att skriva (och arbeta med) transformationsekvationer med hjälp av matriser.
\\\left\{ \matrix {v_x \\ v_y} \right\}\]
De \(\cos \theta\) termerna ligger på matrisdiagonalen medan \(\sin \theta\)termerna ligger utanför diagonalen. Det enda potentiella problemet är att komma ihåg vilken \(\sin \theta\)-term som har ett minustecken. Det är alltid den nedre vänstra termen.
Ovanstående ekvation skrivs i matrisnotation som
\
där \({\bf Q}\) är den vanliga bokstaven som valts för transformationsmatrisen.

Transformations- respektive rotationsmatriser
Om det här ämnet inte redan var svårt nog, bidrar många böcker och webbplatser till förvirringen genom att inte klargöra vad som är fixerat och vad som är roterande. På den här och nästa sidan är det koordinatsystemet som roterar medan objektet förblir fixerat, så termen transformationsmatris används här för att betona detta.
Hursomhelst kommer vi senare att ta upp situationer där objektet roterar medan koordinatsystemet förblir fixerat. I detta scenario kommer termen rotationsmatris att användas för att betona att objektet roterar.
Mycket förvirring uppstår på grund av det fantastiska faktum att varje matris (transformation och rotation) bara är transponeringen av den andra! De ser alltså extremt lika ut. I tvådimensionella problem är den enda praktiska skillnaden om minustecknet framför \(\sin \theta\) står på \(q_{12}\)-termen eller \(q_{21}\)-termen.
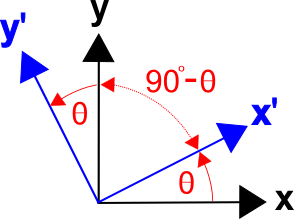
Det finns en allmän metod för att formulera transformationsmatriser som bygger på cosinussatserna av vinklarna mellan axlarna i de två koordinatsystemen, dvs. riktningskosinussatserna. (Detta gäller även 3D-transformationer.)Transformationsmatrisen kan skrivas som
\\\]
där \((x’,x)\) representerar vinkeln mellan axlarna \(x’\) och \(x\),\((x’,y)\) är vinkeln mellan axlarna \(x’\) och \(y\), osv.
Vinkeln mellan \(x’\) och \(y\) är \((90^\circ – \theta)\), och \(\cos(x’,y) = \cos(90^\circ – \theta) = \sin \theta\).
På samma sätt är vinkeln mellan \(y’\) och \(x\) \((90^\circ + \theta)\), och \(\cos(y’,x) = \cos(90^\circ + \theta) = -\sin \theta\).
Tensornotation
Koordinattransformationen skrivs i sensornotation som
\
där \(\(\lambda_{ij}\) är transformationsmatrisen \({\bf Q}\). (Jag vet inte varför \({\bf Q}\) används i matrisnotering, men \(\lambda_{ij}\), inte \(q_{ij}\), används i tensornotering.) \(\lambda_{ij}\) definieras som
Till exempel, om \(i = 1\) och \(j = 2\), så är
\(\lambda_{ij}\) riktningskosinus av vinkeln mellan \(x’_i\) axeln och \(x_j\) axeln. Återigen är detta lika tillämpligt på 3D-transformationer också.
2-D-koordinattransformationer av tensorer
Detta avsnitt kommer att presentera vad och hur tensortransformationer går till. varför får vänta till senare.
Koordinattransformationer av tensorer av 2:a rang involverar samma \({\bf Q}\)-matris som vektortransformationer. En transformation av spänningensorn \(\boldsymbol{\sigma}\), från referenskoordinatsystemet \(x-y\) till \(\boldsymbol{\sigma’}\) i ett nytt \(x’-y’\)-system görs på följande sätt.
\
Skrivning av matriserna explicit ger
\ = \vänster \vänster \vänster \vänster \vänster \]
(Observera att spänningensorn alltid är symmetrisk, även efter transformationer.)
Multiplicering av matriserna ger
\
Dessa tre ekvationer är exakt 2D-transformen av en spänningstenor som uppstår när man summerar krafter på ett differentialelement och påtvingar jämvikt. Detta representeras också av Mohrs cirkel.
Tensornotation
Koordinattransformationen skrivs i sensornotation som
\
Som vanligt ger sensornotationen extra insikt i processen. Den här gången kommer insikten från subscripts på lambdas. Varje lambda kopplar effektivt ihop ett subscript på \(\boldsymbol{\sigma’}\) med ett på \(\boldsymbol{\sigma}\).Detta gäller oavsett tensorens rang.
3-D koordinattransformationer av vektorer
Många av de allmänna ekvationer som används i 2D-transformationer är också tillämpliga i 3D.Exempel är
\
Bara nu är detaljerna annorlunda. Vektorerna har z-komponenter och transformationsmatriserna är 3×3 i stället för 2×2.
\\]
\\\]
\\left\{ \matrix { v_x \\ v_y \\ v_z } \right\}\]
3-D koordinattransformationer av tensorer
Ännu en gång ändras inte reglerna, bara detaljerna gör det.
Om matriserna skrivs ut uttryckligen får man
\\ = \left\left\left\left\]
Denna webbsida utför koordinattransformationer på 3D-tensorer. Prova den.
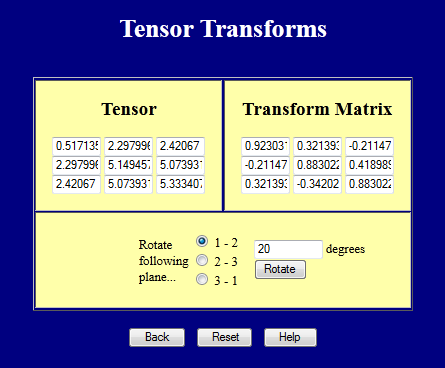
Koordinattransformationer av tensorer av 4:e rang
Vi kommer att se i avsnittet om Hookes lag att styvhetensorn är av 4:e rang, dvs. 3x3x3x3x3 (inte 4×4). Den skrivs som \(C_{ijkl}\) eftersom den relaterar varje töjningskomponent, \(\epsilon_{kl}\), till varje spänningskomponent, \(\sigma_{ij}\),dvs, \(\sigma_{ij} = C_{ijkl} \epsilon_{kl}\).Lagen om koordinattransformation för den fjärde rangens styvhetstenor kan enkelt skrivas i tensor-notation som
\
Tensorekvationen visar hur transformationen skall skrivas i matrisnotation.
\
Sammanfattning
Koordinattransformationen av en vektor i matris- och tensornotation är
\
Koordinattransformationen av en tensor i matris- och tensornotation är
\
Notera att \({\bf Q}\) och \(\lambda_{ij}\) är samma transformationsmatris.
I 2D definieras \({\bf Q}\) och \(\lambda_{ij}\) som
\\\]
som är ett specialfall av den mer allmänna 3D-formen
\\]
.