Proportionellt är bara ett sätt att reagera på ett fel i systemet. Problemet med proportionell reglering är att den inte kan upptäcka trender och anpassa sig till dem. Detta är den integrala styrningens uppgift.
Det finns en annan exempelgraf över felet i ett system över tiden till vänster i figur 6. Återigen kan det handla om en robots avstånd till ett objekt, eller om vätskenivån i en tank eller temperaturen i en fabriksugn. Kanske fortsätter det mål som roboten följer att gå bort från roboten i en hastighet som roboten inte hinner ikapp. Kanske är ugnsdörrens tätning sliten, kanske är vätskeuttaget från tanken ovanligt stort. Oavsett orsaken kan den proportionella roboten inte upptäcka och korrigera problemet eftersom den inte är konstruerad för att reagera på trender. Det är där integralstyrning kommer in i bilden.
Integral mäter området mellan felvärdena och tidsaxeln. Om felet inte återgår till noll blir felets area större och större. Den högra sidan i figur 6 visar hur integralutgången kan reagera på denna typ av trend. När arean mellan felkurvan och tidsaxeln ökar, ökar utgången proportionellt mot denna area. Som ett resultat driver utgången ställdonet hårdare och hårdare för att korrigera felet.
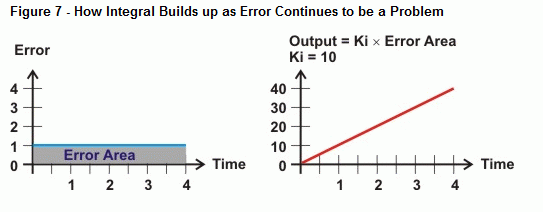
Så vad händer när felet inte är en rak linje, som kurvan i figur 8? Det är vad kalkyloperationen integration bestämmer, arean mellan en kurva och en axel. När det gäller integralreglering ökar arean under kurvan när mer tid går med ett fel, och därmed också det värde som integralberäkningen kommer att använda för att driva mot systemfelet. Om felkurvan sjunker under tidsaxeln subtraheras uppbyggnaden av negativt område från uppbyggnaden av positivt område. När den är rätt inställd kan integralkontrollen hjälpa systemet att närma sig ett fel på noll.
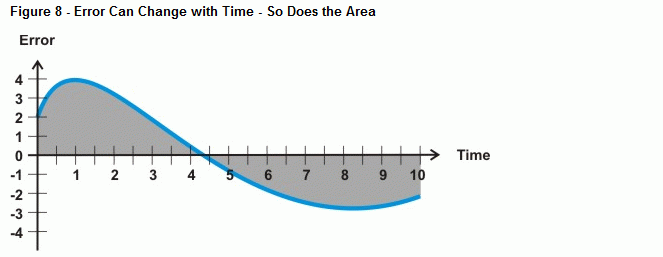
Basic Stamp kan approximera felet under kurvan med hjälp av numerisk integration. Figur 9 visar hur du kan approximera felet under en kurva genom att addera arean av ett gäng små rektanglar mellan felkurvan och tidsaxeln. Arean i varje ruta är felet multiplicerat med tiden mellan mätningarna. Genom att addera alla rutornas areor får du en approximation av arean under kurvan.
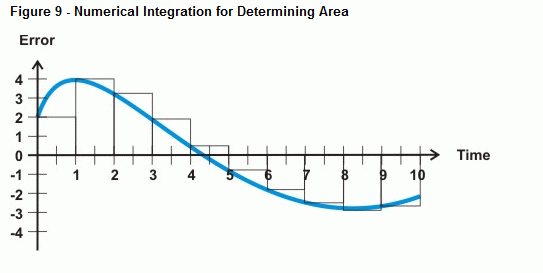
Så länge dina mätningar är jämnt fördelade kan du kalla bredden på varje ruta för värdet 1. Detta gör matematiken mycket enklare än att försöka ta hänsyn till 20 ms mellan proverna, 5 minuter mellan proverna, eller vad din provtagningsfrekvens nu än visar sig vara. I stället för att multiplicera felet med tidsinkrementet mellan proverna och sedan lägga till nästa fel multiplicerat med tiden, kan du bara multiplicera varje felprov med en tid på 1. Resultatet är att du bara kan hålla en löpande summa av felmätningar för din integralberäkning. Här är ett exempel på hur man gör detta med PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
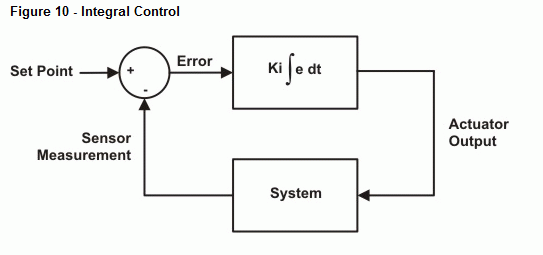
Nästa exempelprogram utför numerisk integration på felsignalen och justerar utgången därefter. Precis som med proportionell reglering finns det en konstant som skalar integrationsutgången till det önskade värdet. För enkelhetens skull använder vi 10 igen för Ki. Figur 10 visar ett blockdiagram över styrslingan. Termen Kp ∫ edt avser Kp multiplicerat med felets integral över tiden. Med andra ord, Kp multiplicerat med den ackumulerade ytan mellan felkurvan och tidsaxeln.
Exempelprogram – IntegralAlgorithm.bs2
- Inför, spara och kör IntegralAlgorithm.bs2.
- Inför den här sekvensen av värden i fönstret för sändning i Debug Terminal: 3 3 3 3 3 3 3 3 3. Lägg märke till hur integralutmatningen blir större varje gång 3 upprepas. Det är integralens uppgift, att upptäcka trender och öka drivkraften för att korrigera den vid behov.
- Prova nu denna sekvens: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. Arean under denna kurva är 0 eftersom den negativa arean är densamma som den positiva arean. Det är också vad integralberäkningen kommer fram till när du har skrivit in sekvensen.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Hur IntegralAlgorithm.bs2 fungerar
Detta program är en ProportionalAlgorithm.bs2 modifierad så att den utför integralberäkningen istället. Det finns nu två olika typer av fel att hålla reda på, så där utökades felvariabelmatrisen till två element. Variabeln error(0) spårar det aktuella felet och error(1) spårar det ackumulerade felet. Konstanterna Current CON 0 och Accumulator CON 1 gör bokföringen lite vettigare med error(current) och error(accumulator).
Den andra ändringen som gjordes är att felet ackumuleras och att integralutgången beräknas med dessa två påståenden:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Din tur – klampa in integralutgången
Som du kanske har förstått av att du upprepade gånger har skrivit in 3 i felsökningsterminalen, så kan integraldrivningens utgång verkligen börja springa iväg. Du kan använda operatörerna MIN och MAX för att hindra integralstyrningen från att gå över gränsen med utgången. Låt oss upprepa servoförskjutningsaktiviteten och begränsa utgången från 650 till 850.
- Förändra påståendet drive = i till drive = i + Offset MIN 650 MAX 850.
- Kör programmet och kontrollera att den integrala utgången är begränsad till värden mellan 650 och 850. Prova att skriva in 2 upprepade gånger, sedan -2 upprepade gånger.