Less…
![]()
Det finns många formler för ![]() av många typer. Bland annat ingår serier, produkter, geometriska konstruktioner, gränser, speciella värden och pi-iterationer.
av många typer. Bland annat ingår serier, produkter, geometriska konstruktioner, gränser, speciella värden och pi-iterationer.
![]() är intimt förknippat med egenskaperna hos cirklar och sfärer. För en cirkel med radie
är intimt förknippat med egenskaperna hos cirklar och sfärer. För en cirkel med radie ![]() , ges omkretsen och arean av
, ges omkretsen och arean av
|
(1)
|
|||
|
(2)
|
Samma sak för en sfär med radie ![]() , är ytan och volymen
, är ytan och volymen
|
(3)
|
|||
|
(4)
|
En exakt formel för ![]() i termer av de inversa tangenterna av enhetsbråk är Machins formel
i termer av de inversa tangenterna av enhetsbråk är Machins formel
|
(5)
|
Det finns tre andra Machin-liknande formler,samt tusentals andra liknande formler med fler termer.
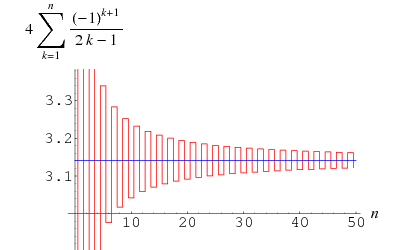
Gregory och Leibniz fann
|
(6)
|
|||
|
(7)
|
(Wells 1986, s. 50), som är känd som Gregoryserien och kan erhållas genom att sätta in ![]() i Leibnizserien för
i Leibnizserien för ![]() . Felet efter den
. Felet efter den ![]() de termen i denna serie i Gregory-serien är större än
de termen i denna serie i Gregory-serien är större än ![]() så denna summa konvergerar så långsamt att 300 termer inte räcker för att beräkna
så denna summa konvergerar så långsamt att 300 termer inte räcker för att beräkna ![]() korrekt till två decimaler! Den kan dock omvandlas till
korrekt till två decimaler! Den kan dock omvandlas till
|
(8)
|
där ![]() är Riemanns zeta-funktion (Vardi 1991, pp. 157-158; Flajolet och Vardi 1996), så att felet efter
är Riemanns zeta-funktion (Vardi 1991, pp. 157-158; Flajolet och Vardi 1996), så att felet efter ![]() termer är
termer är ![]() .
.
En oändlig summeserie till Abraham Sharp (ca. 1717) ges av
|
(9)
|
(Smith 1953, s. 311). Ytterligare enkla serier där ![]() förekommer är
förekommer är
|
(10)
|
|||
|
(11)
|
|||
|
(12)
|
|||
|
(13)
|
|||
|
(14)
|
|||
|
(15)
|
|||
|
(16)
|
|||
|
(17)
|
(Wells 1986, s. 53).
I 1666, Newton använde en geometrisk konstruktion för att härleda formeln
|
(18)
|
|||
|
(19)
|
som han använde för att beräkna ![]() (Wells 1986, s. 50; Borwein et al. 1989; Borwein och Bailey 2003, s. 105-106). Koefficienterna kan hittas från integralen
(Wells 1986, s. 50; Borwein et al. 1989; Borwein och Bailey 2003, s. 105-106). Koefficienterna kan hittas från integralen
|
(20)
|
|||
|
(21)
|
genom att ta serieexpansionen av ![]() kring 0, obtaining
kring 0, obtaining
|
(22)
|
(OEIS A054387 och A054388). Om man använder Eulers konvergensförbättrande omvandling får man
|
(23)
|
|||
|
(24)
|
|||
|
(25)
|
(Beeler et al. 1972, punkt 120).
Detta motsvarar att sätta in ![]() i potensserien för den hypergeometriska funktionen
i potensserien för den hypergeometriska funktionen ![]() ,
,
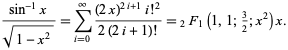 |
(26)
|
Trots konvergensförbättringen konvergerar serien (◇) vid endast en bit/termin. På bekostnad av en kvadratrot har Gosper noterat att ![]() ger 2 bitar/term,
ger 2 bitar/term,
|
(27)
|
och ![]() ger nästan 3.39 bitar/termin,
ger nästan 3.39 bitar/termin,
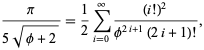 |
(28)
|
där ![]() är det gyllene snittet. Gosper fick också
är det gyllene snittet. Gosper fick också
|
(29)
|
En spikalgoritm för ![]() ges av Rabinowitz och Wagon (1995; Borwein och Bailey 2003, s. 141-142).
ges av Rabinowitz och Wagon (1995; Borwein och Bailey 2003, s. 141-142).
Mer fantastiskt ännu är att ett uttryck i sluten form som ger en algoritm för sifferutvinning som ger siffror på ![]() (eller
(eller ![]() ) i bas-16 har upptäckts av Bailey et al. (Bailey et al. 1997, Adamchik och Wagon 1997),
) i bas-16 har upptäckts av Bailey et al. (Bailey et al. 1997, Adamchik och Wagon 1997),
|
(30)
|
Denna formel, känd som BBP-formeln, upptäcktes med hjälp av PSLQ-algoritmen (Ferguson et al. 1999) och är likvärdig med
|
(31)
|
Det finns en serie formler av BBP-typ för ![]() i potenser av
i potenser av ![]() , De första oberoende formlerna är
, De första oberoende formlerna är
|
(32)
|
|||
|
(33)
|
|||
|
(34)
|
|||
 |
(35)
|
||
 |
(36)
|
||
 |
(37)
|
På samma sätt finns det en rad formler av BBP-typ för ![]() i potenser av
i potenser av ![]() , De första oberoende formlerna är
, De första oberoende formlerna är
|
(38)
|
|||
|
(39)
|
|||
 |
(40)
|
||
 |
(41)
|
||
 |
(42)
|
||
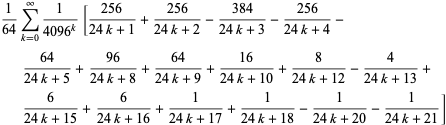 |
(43)
|
||
 |
(44)
|
||
 |
(45)
|
||
 |
(46)
|
||
 |
(47)
|
||
 |
(48)
|
F. Bellard fann den snabbt konvergerande BBP-typformeln
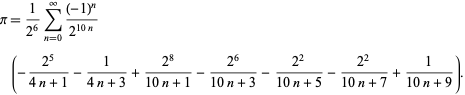 |
(49)
|
En relaterad integral är
|
(50)
|
(Dalzell 1944, 1971; Le Lionnais 1983, s. 22; Borwein, Bailey och Girgensohn 2004, s. 3; Boros och Moll 2004, s. 125; Lucas 2005; Borwein et al. 2007, s. 14). Denna integral var känd av K. Mahler i mitten av 1960-talet och förekommer i en tentamen vid University of Sydney i november 1960 (Borwein, Bailey och Girgensohn, s. 3). Beukers (2000) och Boros och Moll (2004, s. 126) konstaterar att det inte är klart om dessa finns ett naturligt val av rationellt polynom vars integral mellan 0 och 1 ger ![]() , där 333/106 är nästa konvergent. Det finns dock ett integral för den fjärde konvergenten, nämligen
, där 333/106 är nästa konvergent. Det finns dock ett integral för den fjärde konvergenten, nämligen
|
(51)
|
(Lucas 2005; Bailey et al. 2007, s. 219). I själva verket ger Lucas (2005) några andra sådana integraler.
Backhouse (1995) använde identiteten
|
(52)
|
|||
|
(53)
|
|||
|
(54)
|
för positiva heltal ![]() och
och ![]() och där
och där ![]() ,
, ![]() och
och ![]() är rationella konstanter för att generera ett antal formler för
är rationella konstanter för att generera ett antal formler för ![]() . I synnerhet om
. I synnerhet om ![]() , så är
, så är ![]() (Lucas 2005).
(Lucas 2005).
En liknande formel upptäcktes senare av Ferguson, vilket leder till ett tvådimensionellt gitter av sådana formler som kan genereras av dessa två formler som ges av
|
(55)
|
för varje komplext värde av ![]() (Adamchik och Wagon), vilket ger BBP-formeln som specialfall
(Adamchik och Wagon), vilket ger BBP-formeln som specialfall ![]() .
.
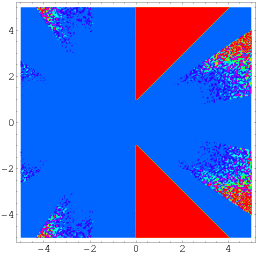
En ännu mer allmän identitet som beror på Wagon ges av
 |
(56)
|
(Borwein och Bailey 2003, p. 141), som gäller över ett område av det komplexa planet som utesluter två triangulära delar som är symmetriskt placerade runt den reella axeln, enligt illustrationen ovan.
En kanske ännu märkligare allmän klass av identiteter ges av
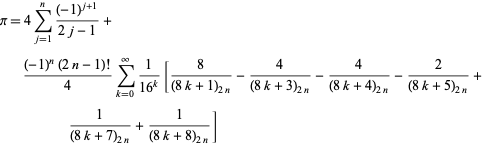 |
(57)
|
som gäller för varje positivt heltal ![]() , där
, där ![]() är en Pochhammer-symbol (B. Cloitre, pers. komm, 23 januari 2005). Ännu mer häpnadsväckande är att det finns en nära analog formel för den naturliga logaritmen av 2.
är en Pochhammer-symbol (B. Cloitre, pers. komm, 23 januari 2005). Ännu mer häpnadsväckande är att det finns en nära analog formel för den naturliga logaritmen av 2.
Efter upptäckten av BBP-formeln med 16-siffriga siffror i basen och relaterade formler undersöktes liknande formler i andra baser. Borwein, Bailey och Girgensohn (2004) har nyligen visat att ![]() inte har någon Machin-typ BBP-arktangentformel som inte är binär, även om detta inte utesluter att det finns ett helt annat system för algoritmer för sifferutvinning i andra baser.
inte har någon Machin-typ BBP-arktangentformel som inte är binär, även om detta inte utesluter att det finns ett helt annat system för algoritmer för sifferutvinning i andra baser.
S. Plouffe har utarbetat en algoritm för att beräkna den ![]() te siffran i
te siffran i ![]() i vilken bas som helst i
i vilken bas som helst i ![]() steg.
steg.
En mängd ytterligare identiteter som beror på Ramanujan, Catalan och Newton ges av Castellanos (1988ab, s. 86-88), inklusive flera som involverar summor av Fibonacci-tal. Ramanujan fann
 |
(58)
|
(Hardy 1923, 1924, 1999, p. 7).
Plouffe (2006) fann den vackra formeln
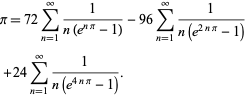 |
(59)
|
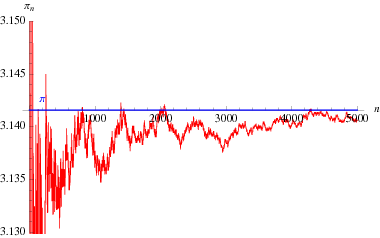
En intressant formel för oändlig produkt som beror på Euler och som relaterar ![]() och det
och det ![]() te primtalet
te primtalet ![]() är
är
 |
(60)
|
||
|
(61)
|
(Blatner 1997, p. 119), plottat ovan som en funktion av antalet termer i produkten.
En metod som liknar Archimedes’ kan användas för att uppskatta ![]() genom att börja med en
genom att börja med en ![]() -gon och sedan relatera arean av efterföljande
-gon och sedan relatera arean av efterföljande ![]() -gons. Låt
-gons. Låt ![]() vara vinkeln från centrum av ett av polygonens segment,
vara vinkeln från centrum av ett av polygonens segment,
|
(62)
|
då
| pi=(2sin(2beta))/((n-3)produkt_(k=0)^(infty)cos(2^(-k)beta)) |
(63)
|
(Beckmann 1989, pp. 92-94).
Vieta (1593) var den förste som gav ett exakt uttryck för ![]() genom att ta
genom att ta ![]() i ovanstående uttryck, vilket ger
i ovanstående uttryck, vilket ger
|
(64)
|
vilket leder till en oändlig produkt av nestedradikaler,
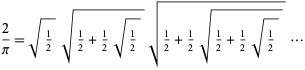 |
(65)
|
(Wells 1986, s. 50; Beckmann 1989, s. 95). Det bevisades dock inte rigoröst att detta uttryck konvergerar förrän Rudio 1892.
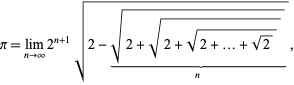
En besläktad formel ges av
 |
(66)
|
som kan skrivas
|
(67)
|
där ![]() definieras med hjälp av iterationen
definieras med hjälp av iterationen
 |
(68)
|
med ![]() (J. Munkhammar, pers. komm, 27 april 2000). Formeln
(J. Munkhammar, pers. komm, 27 april 2000). Formeln
 |
(69)
|
är också nära besläktad.
En vacker formel för ![]() ges av
ges av
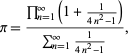 |
(70)
|
där täljaren är en form av Wallisformeln för ![]() och nämnaren är en teleskopisk summa med summa 1/2 eftersom
och nämnaren är en teleskopisk summa med summa 1/2 eftersom
|
(71)
|
(Sondow 1997).
Ett särskilt fall av Wallisformeln ger
|
(72)
|
(Wells 1986, s. 50). Denna formel kan också skrivas
 |
(73)
|
varvid ![]() betecknar en binomialkoefficient och
betecknar en binomialkoefficient och ![]() är gammafunktionen (Knopp 1990). Euler fick
är gammafunktionen (Knopp 1990). Euler fick
|
(74)
|
vilket följer av det speciella värdet av Riemanns zeta-funktion ![]() . Liknande formler följer av
. Liknande formler följer av ![]() för alla positiva heltal
för alla positiva heltal ![]() .
.
En oändlig summa som beror på Ramanujan är
|
(75)
|
(Borwein et al. 1989; Borwein och Bailey 2003, s. 109; Bailey et al.2007, s. 44). Ytterligare summor ges i Ramanujan (1913-14),
|
(76)
|
och
|
(77)
|
|||
|
(78)
|
(Beeler et al. 1972, punkt 139; Borwein et al. 1989; Borwein och Bailey 2003, s. 108; Bailey et al. 2007, s. 44). Ekvation (78) härleds från en modulär identitet av ordning 58, även om en första härledning inte presenterades före Borwein och Borwein (1987). Ovanstående serier ger båda
|
(79)
|
(Wells 1986, s. 54) som första approximation och ger ungefär 6 respektive 8 decimaler per term. Sådana serier existerar på grund av rationaliteten hos olika modulära invarianter.
Seriens allmänna form är
|
(80)
|
där ![]() är en binär kvadratisk formdiskriminant,
är en binär kvadratisk formdiskriminant, ![]() är j-funktionen,
är j-funktionen,
|
(81)
|
|||
|
(82)
|
och ![]() är Eisenstein-serier. Ett klassnummer
är Eisenstein-serier. Ett klassnummer ![]() fält innefattar
fält innefattar ![]() algebraiska heltal av 2711>th grad av konstanterna
algebraiska heltal av 2711>th grad av konstanterna ![]() ,
, ![]() och
och ![]() . Av alla serier som endast består av heltalstermer motsvarar den som ger flest numeriska siffror på kortast möjliga tid den största klassnummer 1-diskriminanten
. Av alla serier som endast består av heltalstermer motsvarar den som ger flest numeriska siffror på kortast möjliga tid den största klassnummer 1-diskriminanten ![]() och formulerades av bröderna Chudnovsky (1987). Den 163 som förekommer här är samma som förekommer i det faktum att
och formulerades av bröderna Chudnovsky (1987). Den 163 som förekommer här är samma som förekommer i det faktum att ![]() (Ramanujans konstant) är mycket nära ett heltal. På samma sätt kommer faktorn
(Ramanujans konstant) är mycket nära ett heltal. På samma sätt kommer faktorn ![]() från j-funktionsidentiteten för
från j-funktionsidentiteten för ![]() . Serien ges av
. Serien ges av
|
(83)
|
|||
|
(84)
|
(Borwein och Borwein 1993; Beck och Trott; Bailey et al. 2007, s. 44). Denna serie ger 14 siffror exakt per term. Samma ekvation i en annan form gavs av bröderna Chudnovsky (1987) och används av Wolfram Language för att beräkna ![]() (Vardi 1991; Wolfram Research),
(Vardi 1991; Wolfram Research),
|
(85)
|
där
|
(86)
|
|||
|
(87)
|
|||
|
(88)
|
Den bästa formeln för klass nummer 2 (största diskriminanten ![]() ) är
) är
|
(89)
|
här
|
(90)
|
|||
|
(91)
|
|||
|
(92)
|
(Borwein och Borwein 1993). Denna serie lägger till cirka 25 siffror för varje ytterligare term. Den snabbast konvergerande serien för klass nummer 3 motsvarar ![]() och ger 37-38 siffror per term. Den snabbast konvergerande serien för klass nummer 4 motsvarar
och ger 37-38 siffror per term. Den snabbast konvergerande serien för klass nummer 4 motsvarar ![]() och är
och är
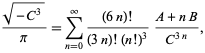 |
(93)
|
här
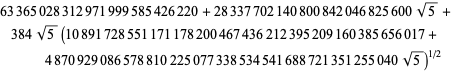 |
(94)
|
||
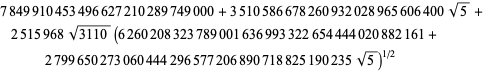 |
(95)
|
||
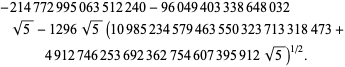 |
(96)
|
Detta ger 50 siffror per term. Borwein och Borwein (1993) har utvecklat en allmän algoritm för att generera sådana serier för ett godtyckligt klasstal.
En fullständig förteckning över Ramanujans serier för ![]() som hittats i hans andra och tredje anteckningsbok ges av Berndt (1994, pp. 352-354),
som hittats i hans andra och tredje anteckningsbok ges av Berndt (1994, pp. 352-354),
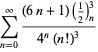 |
(97)
|
||
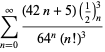 |
(98)
|
||
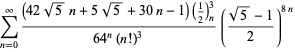 |
(99)
|
||
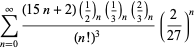 |
(100)
|
||
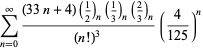 |
(101)
|
||
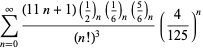 |
(102)
|
||
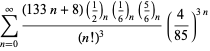 |
(103)
|
||
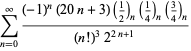 |
(104)
|
||
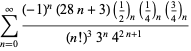 |
(105)
|
||
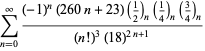 |
(106)
|
||
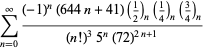 |
(107)
|
||
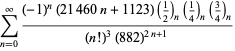 |
(108)
|
||
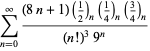 |
(109)
|
||
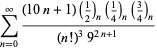 |
(110)
|
||
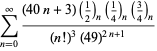 |
(111)
|
||
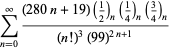 |
(112)
|
||
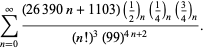 |
(113)
|
Dessa ekvationer bevisades först av Borwein och Borwein (1987a, s. 177-187). Borwein och Borwein (1987b, 1988, 1993) bevisade andra ekvationer av denna typ, och Chudnovsky och Chudnovsky (1987) fann liknande ekvationer för andra transcendentala konstanter (Bailey et al. 2007, s. 44-45).
En fullständig lista över oberoende kända ekvationer av denna typ ges av
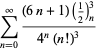 |
(114)
|
||
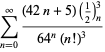 |
(115)
|
||
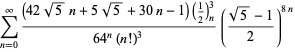 |
(116)
|
||
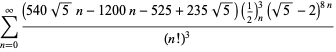 |
(117)
|
||
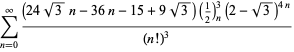 |
(118)
|
för ![]() med icke alternerande tecken,
med icke alternerande tecken,
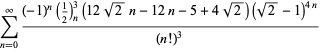 |
(119)
|
||
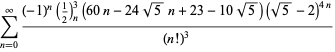 |
(120)
|
||
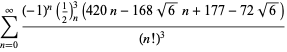 |
(121)
|
||
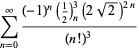 |
(122)
|
för ![]() med omväxlande tecken,
med omväxlande tecken,
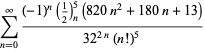 |
(123)
|
||
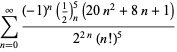 |
(124)
|
för ![]() (Guillera 2002, 2003, 2006),
(Guillera 2002, 2003, 2006),
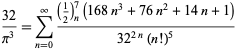 |
(125)
|
för ![]() (Guillera 2002, 2003, 2006), och inga andra för
(Guillera 2002, 2003, 2006), och inga andra för ![]() är kända (Bailey et al. 2007, s. 45-48).
är kända (Bailey et al. 2007, s. 45-48).
Bellard ger den exotiska formeln
 |
(126)
|
where
|
(127)
|
Gasper citerar resultatet
|
(128)
|
där ![]() är en generaliserad hypergeometrisk funktion, och transformerar det till
är en generaliserad hypergeometrisk funktion, och transformerar det till
|
(129)
|
Ett fascinerande resultat som beror på Gosper ges av
|
(130)
|
![]() uppfyller olikheten
uppfyller olikheten
|
(131)
|
D. Terr (pers. komm.) noterade den märkliga identiteten
|
(132)
|
som involverar de första 9 siffrorna i pi.
.