Rotationskinematik - Fysik 298

”Män talar om att döda tiden, medan tiden tyst dödar dem”
Dion Boucicault – London Assurance (1841)

Hittills har vi betraktat partikelns kinematik och dynamik, inklusive translations- och cirkelrörelse samt translationsrörelsen hos system av partiklar (särskilt stela kroppar) i termer av rörelsen hos systemets masscentrum (kropp). I det senare fallet kan vi föreställa oss att föremålets hela massa befinner sig i masscentrumet när det gäller externa translationella krafter.

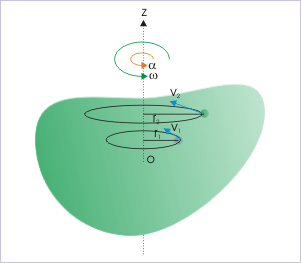Nästa steg är att betrakta rotationen av en stel kropp kring en fast rotationsaxel. Observera att eftersom vi betraktar en stel kropp förblir varje partikel i kroppen fast i förhållande till de andra. Detta innebär att i en sådan rotationsrörelse rör sig varje partikel i en cirkel vars centrum ligger på rotationsaxeln. I diagrammet till höger roterar föremålet runt z-axeln; de två provpartiklarna rör sig i cirklar med radierna r1 och r2. Om vi kan beskriva en partikels cirkelrörelse utan att direkt hänvisa till dess radie, kommer alla partiklar i systemet att beskrivas av samma uppsättning ekvationer. Även om partiklarnas radier är olika är deras vinkelrotationer identiska. Därför är det nödvändigt att införa vinkelvariabler.

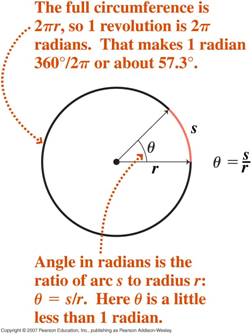
Radianmått för vinklar

Vinkelhastighet (hastighet) och vinkelacceleration

Vinkelhastighet och vinkelacceleration definieras på liknande sätt som hastighet och acceleration. Det finns medelvärden och momentana värden för vardera.

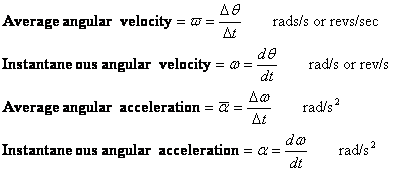
Vinkelacceleration är inte samma sak som centripetalacceleration. Centripetalacceleration beror på en förändring i hastighetens riktning, vinkelacceleration beror på en förändring i hastighetens storlek (genom rotationsvinkeln).

Precis som i translationsfallet är skillnaden mellan vinkelhastighet och vinkelhastighet riktning. Vinkelhastigheten måste innefatta en rotationsriktning runt den aktuella axeln. Exempelvis är 10 rad/s medurs om x-axeln en vinkelhastighet, 10 rad/s om x-axeln är en vinkelhastighet.

Rotationskinematiska ekvationer

I direkt analogi med de translationskinematiska ekvationerna kan cirkelrörelse kring en enda axel under konstant vinkelacceleration beskrivas med följande fyra ekvationer,

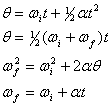
där vi har gjort utbytena,

Bemärk att på samma sätt som +x kan definieras godtyckligt till höger, kan det positiva värdet av theta definieras som med eller moturs.

Samband mellan vinkel- och translationsvariabler

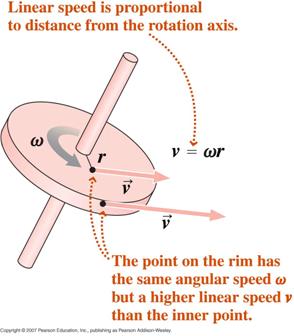Med utgångspunkt i definitionen av radianmåttet kan vi genom att differentiera med avseende på tiden visa att,

varvid v är den tangentiella hastigheten och a är den tangentiella accelerationen.

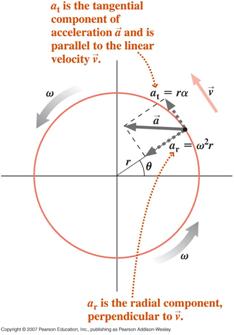
En partikel som utför en cirkelrörelse med varierande vinkelhastighet (ojämn cirkelrörelse) kommer att uppleva två accelerationskomponenter, en tangentiell komponent på grund av den förändrade storleken på dess hastighet och en radiell (centripetal) komponent på grund av den förändrade riktningen på dess hastighet

Partikelns nettoacceleration är vektorsumman av dessa två komponenter enligt nedan.

För din information…

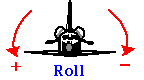
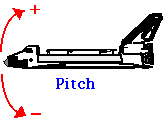
Samtidig rotation om mer än en axel kan betraktas på samma sätt som projektilrörelse, där vi utvidgade vår 1D translationella diskussion till 2D rörelse. I flygtekniska tillämpningar beskrivs rotationer kring de tre axlarna som Roll, Pitch och Yaw.