
Matematik handlar om ett enormt antal begrepp som är mycket viktiga men samtidigt komplexa och tidskrävande. Python tillhandahåller dock det fullfjädrade SciPy-biblioteket som löser detta problem för oss. I den här SciPy-handledningen kommer du att lära dig hur du använder det här biblioteket tillsammans med några funktioner och deras exempel.
För att gå vidare, ta en titt på alla ämnen som diskuteras i den här artikeln:
- Vad är SciPy?
- NumPy vs SciPy
- Underpaket i SciPy
- Grundläggande funktioner
- Specialfunktioner
- Integrationsfunktioner
- Optimeringsfunktioner
- Fouriertransformationsfunktioner
- Signal. Processing Functions
- Linear Algebra
- Sparse Eigenvalues
- Spatial Data Structures and Algorithms
- Multidimensional Image Processing Functions
- File IO
Så låt oss komma igång. 🙂
SciPy är ett Pythonbibliotek med öppen källkod som används för att lösa vetenskapliga och matematiska problem. Det bygger på NumPy-tillägget och gör det möjligt för användaren att manipulera och visualisera data med ett stort antal kommandon på hög nivå. Som tidigare nämnts bygger SciPy på NumPy och om du importerar SciPy behöver du därför inte importera NumPy.
NumPy vs SciPy
Både NumPy och SciPy är Pythonbibliotek som används för använd matematisk och numerisk analys. NumPy innehåller array-data och grundläggande operationer som sortering, indexering osv. medan SciPy består av all numerisk kod. Även om NumPy tillhandahåller ett antal funktioner som kan hjälpa till att lösa linjär algebra, Fouriertransformationer osv. är SciPy det bibliotek som faktiskt innehåller fullfjädrade versioner av dessa funktioner tillsammans med många andra. Om du gör vetenskapliga analyser med hjälp av Python måste du dock installera både NumPy och SciPy eftersom SciPy bygger på NumPy.
Underpaket i SciPy:
SciPy har ett antal underpaket för olika vetenskapliga beräkningar som visas i följande tabell:

För en detaljerad beskrivning kan du dock följa den officiella dokumentationen.
Dessa paket måste importeras exklusivt innan de används. Till exempel:
from scipy import cluster
För att titta på var och en av dessa funktioner i detalj ska vi först ta en titt på de funktioner som är gemensamma för både NumPy och SciPy.
Interaktion med NumPy:
SciPy bygger på NumPy och därför kan du använda dig av NumPy-funktioner i sig själv för att hantera matriser. Om du vill veta mer om dessa funktioner kan du helt enkelt använda funktionerna help(), info() eller source().
help():
För att få information om en funktion kan du använda funktionen help(). Det finns två sätt som denna funktion kan användas på:
- utan parametrar
- med parametrar
Här är ett exempel som visar båda ovanstående metoder:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
När du utför ovanstående kod returnerar den första help() informationen om klusterundermodulen. Den andra help() ber användaren att ange namnet på en modul, ett nyckelord etc. som användaren vill söka information om. För att stoppa utförandet av denna funktion skriver du helt enkelt ”quit” och trycker på enter.
info():
Denna funktion returnerar information om de önskade funktionerna, modulerna etc.
scipy.info(cluster)
source():
Källkoden returneras endast för objekt som är skrivna i Python. Den här funktionen returnerar inte användbar information om metoderna eller objekten är skrivna på något annat språk, t.ex. C. Men om du vill använda dig av den här funktionen kan du göra det på följande sätt:
scipy.source(cluster)
Specialfunktioner:
SciPy tillhandahåller ett antal specialfunktioner som används inom matematisk fysik, t.ex. elliptiska, bekvämlighetsfunktioner, gamma, beta osv. För att leta efter alla funktioner kan du använda funktionen help() som beskrivs tidigare.
Exponential- och trigonometriska funktioner:
SciPys paket Special Function tillhandahåller ett antal funktioner genom vilka du kan hitta exponenter och lösa trigonometriska problem.
Konsultera följande exempel:
EXEMPEL:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
UTGÅNG:
1000.0
8.0
1.0
0.7071067811865475
Det finns många andra funktioner som finns i SciPys specialfunktionspaket som du kan prova själv.
Integrationsfunktioner:
SciPy tillhandahåller ett antal funktioner för att lösa integraler. SciPy är ett lager av funktioner för att lösa alla typer av integralproblem, allt från vanlig differentiell integrator till att använda trapezoidregler för att beräkna integraler.
Allmän integration:
SiPy tillhandahåller en funktion som heter quad för att beräkna integralen av en funktion som har en variabel. Gränserna kan vara ( ) för att ange oändliga gränser. Syntaxen för funktionen quad() är följande:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Här kommer funktionen att integreras mellan gränserna a och b (kan också vara oändlig).
EXEMPEL:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
I exemplet ovan utvärderas funktionen ”a” mellan gränsvärdena 0, 1. När koden exekveras får du följande utdata.
UTGÅNG:
(3,9086503371292665, 4,3394735994897923e-14)
Dubbelintegralfunktion:
SciPy tillhandahåller dblquad som kan användas för att beräkna dubbla integraler. En dubbelintegral består som många av oss vet av två reella variabler. Funktionen dblquad() tar funktionen som ska integreras som parameter tillsammans med fyra andra variabler som definierar gränserna och funktionerna dy och dx.
EXEMPEL:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
UTLÄGGNING:
-1.333333333333333335, 1.4802973661668755e-14)
SciPy tillhandahåller olika andra funktioner för att utvärdera trippelintegraler, n-integraler, Romberg-integraler etc. som du kan utforska ytterligare i detalj. För att hitta alla detaljer om de nödvändiga funktionerna kan du använda hjälpfunktionen.
Optimeringsfunktioner:
Scipy.optimize tillhandahåller ett antal vanligt förekommande optimeringsalgoritmer som kan ses med hjälp av hjälpfunktionen.
Den består i princip av följande:
- Obegränsad och begränsad minimering av multivariata skalära funktioner dvs. minimera (t.ex. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, etc)
- Globala optimeringsrutiner (t.ex. Differential_evolution, dual_annealing, etc)
- Minimering av minsta kvadraters värden och kurvanpassning (t.ex. least_squares, curve_fit, etc)
- Skalära univariata funktioner minimerar och hittar rötter (t.ex. minimize_scalar och root_scalar)
- Multivariata ekvationssystemlösare som använder algoritmer som hybrid Powell, Levenberg-Marquardt.
Rosenbrook-funktion:
Rosenbrook-funktionen ( rosen) är ett testproblem som används för gradientbaserade optimeringsalgoritmer. Den definieras på följande sätt i SciPy:

EXEMPEL:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
UTLÄGG: 7371.039999999999945
Nelder-Mead:
Nelder-Mead-metoden är en numerisk metod som ofta används för att hitta min/max för en funktion i ett flerdimensionellt rum. I följande exempel används minimera-metoden tillsammans med Nelder-Mead-algoritmen.
EXEMPEL:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
UTPUT: array()
Interpoleringsfunktioner:
Inom området numerisk analys hänvisar interpolering till att konstruera nya datapunkter inom en uppsättning kända datapunkter. SciPy-biblioteket består av ett underpaket med namnet scipy.interpolate som består av spline-funktioner och klasser, endimensionella och flerdimensionella (univariata och multivariata) interpolationsklasser etc.
Univariabel interpolation:
Univariell interpolation är i princip ett område för kurvanpassning där man hittar den kurva som ger en exakt passning till en serie av tvådimensionella datapunkter. SciPy tillhandahåller interp1d-funktionen som kan användas för att producera univariat interpolation.
EXEMPEL:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
UTGÅNG:
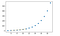
Multivariat interpolation:
Multivariat interpolation (rumslig interpolation ) är en typ av interpolation på funktioner som består av fler än en variabel. Följande exempel visar ett exempel på
Interpolering över ett 2-dimensionellt rutnät med hjälp av funktionen interp2d(x, y, z) i princip kommer att använda x, y, z-matriser för att approximera någon funktion interp2d-funktionen. f: ”z = f(x, y)” och returnerar en funktion vars anropsmetod använder splineinterpolation för att hitta värdet av nya punkter.
EXEMPEL:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
UTGÅNG:

Fouriertransformationsfunktioner:
Fourieranalys är en metod som handlar om att uttrycka en funktion som en summa av periodiska komponenter och att återskapa signalen från dessa komponenter. Funktionerna fft kan användas för att återge den diskreta Fouriertransformen för en reell eller komplex sekvens.
EXEMPEL:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
UTGÅNG:
På samma sätt kan du hitta inversen av detta genom att använda ifft-funktionen på följande sätt:
EXEMPEL:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
UTLÄSNING:
Signalbehandlingsfunktioner:
Signalbehandling handlar om att analysera, modifiera och syntetisera signaler som ljud, bilder osv. SciPy tillhandahåller några funktioner med hjälp av vilka du kan utforma, filtrera och interpolera endimensionella och tvådimensionella data.
Filtrering:
För att filtrera en signal tar du i princip bort oönskade komponenter från den. För att utföra ordnad filtrering kan du använda funktionen order_filter. Denna funktion utför i princip ordnad filtrering på en array. Syntaxen för denna funktion är följande:
SYNTAX:
order_filter(a, domain, rank)
a = N-dimensionell inmatningsmatris
domän = maskmatris som har samma antal dimensioner som `a`
rank = icke-negativt tal som väljer element från listan efter det att den har sorterats (0 är det minsta följt av 1…)
EXEMPEL:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
Den scipy.signal-underpaketet består också av olika funktioner som kan användas för att generera vågformer. En sådan funktion är chirp. Den här funktionen är en frekvens-svept cosinusgenerator och syntaxen är följande:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
UTLÄGG:

Linjär algebra:
Linjär algebra behandlar linjära ekvationer och deras representationer med hjälp av vektorrum och matriser. SciPy bygger på ATLAS LAPACK- och BLAS-biblioteken och är extremt snabb när det gäller att lösa problem som rör linjär algebra. Förutom alla funktioner från numpy.linalg tillhandahåller scipy.linalg även ett antal andra avancerade funktioner. Om numpy.linalg inte används tillsammans med ATLAS LAPACK- och BLAS-stödet är scipy.linalg dessutom snabbare än numpy.linalg.
Finnande av inversen av en matris:
Matematiskt sett är inversen av en matris A matrisen så att där är identitetsmatrisen som består av ettor nedför huvuddiagonalen betecknas som B=A-1. I SciPy kan denna invers erhållas med hjälp av linalg.inv-metoden.
EXEMPEL:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
OUTPUT:
]
Finnande av determinanter:
Värdet som härleds aritmetiskt från matrisens koefficienter är känt som determinanten för en kvadratmatris. I SciPy kan detta göras med hjälp av en funktion det som har följande syntax:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
where,
a : (M, M) Är en kvadratisk matris
overwrite_a( bool, valfritt) : Tillåter överskrivning av data i a
check_finite ( bool, valfritt): För att kontrollera om inmatningsmatrisen endast består av ändliga tal
EXEMPEL:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
UTGÅNG: -5.0
Sparse Eigenvalues:
Eigenvalues är en specifik uppsättning skalarer som är kopplade till linjära ekvationer. ARPACK tillhandahåller som gör det möjligt att hitta egenvärden ( egenvektorer ) ganska snabbt. Hela funktionaliteten hos ARPACK är förpackad i två gränssnitt på hög nivå som är scipy.sparse.linalg.eigs och scipy.sparse.linalg.eigsh. eigs. Gränssnittet eigs gör det möjligt att hitta egenvärdena för reella eller komplexa nonsymmetriska kvadratiska matriser medan gränssnittet eigsh innehåller gränssnitt för reella symmetriska eller komplexa hermitiska matriser.
Funktionen eigh löser ett generaliserat egenvärdesproblem för en komplex hermitisk eller reell symmetrisk matris.
EXEMPEL:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
UTLÄGGNING:
Väljda egenvärden :
Complex ndarray :
]
Spatiella datastrukturer och algoritmer:
Spatiella data består i princip av objekt som består av linjer, punkter, ytor osv. SciPys paket scipy.spatial kan beräkna Voronoi-diagram, trianguleringar osv. med hjälp av biblioteket Qhull. Det består också av KDTree-implementeringar för förfrågningar om närmsta grannpunkt.
Delaunay-trianguleringar:
Matematiskt sett är Delaunay-trianguleringar för en uppsättning diskreta punkter i ett plan en triangulering som är sådan att ingen punkt i den givna punktuppsättningen ligger innanför omkretsen av någon triangel.
EXEMPEL:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
UTGÅNG:

Multidimensionella bildbehandlingsfunktioner:
Bildbehandling handlar i grunden om att utföra operationer på en bild för att hämta information eller för att få fram en förbättrad bild från originalbilden. Paketet scipy.ndimage består av ett antal bildbehandlings- och analysfunktioner som är utformade för att arbeta med matriser av godtycklig dimensionalitet.
Konvolution och korrelation:
SciPy tillhandahåller ett antal funktioner som möjliggör korrelation och konvolution av bilder.
- Funktionen correlate1d kan användas för att beräkna endimensionell korrelation längs en given axel
- Funktionen correlate tillåter flerdimensionell korrelation av en given matris med den angivna kärnan
- Funktionen convolve1d kan användas för att beräkna en-dimensionell konvolution längs en given axel
Funktionen convolve möjliggör flerdimensionell konvolution av en given matris med den angivna kärnan
EXEMPEL:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
File IO:
Den scipy.io-paketet tillhandahåller ett antal funktioner som hjälper dig att hantera filer i olika format, t.ex. MATLAB-filer, IDL-filer, Matrix Market-filer etc.
För att använda det här paketet måste du importera det på följande sätt:
import scipy.io as sio
För fullständig information om delpaketet kan du läsa det officiella dokumentet om File IO.
Det här är slutet på den här SciPy-handledningen. Jag hoppas att du har förstått allt klart och tydligt. Se till att du övar så mycket som möjligt.
Om du vill läsa fler artiklar om marknadens mest trendiga teknik som artificiell intelligens, DevOps, etisk hackning, kan du se Edurekas officiella webbplats.
Se upp för andra artiklar i den här serien som kommer att förklara olika andra aspekter av Python och datavetenskap.
1. Machine Learning Classifier in Python
2. Python Scikit-Learn Cheat Sheet
3. Verktyg för maskininlärning
4. Python Libraries For Data Science And Machine Learning
5. Chatbot In Python
6. Python Collections
7. Python Modules
8. Python developer Skills
9. Intervjufrågor och svar om OOPs
10. CV för en Pythonutvecklare
11. Utforskande dataanalys i Python
12. Ormspel med Pythons sköldpaddsmodul
13. Pythonutvecklarens lön
14. Huvudkomponentanalys
15. Python vs C++
16. Scrapy Tutorial
17. Webbskrapning med Python
18. Metod för regression med minsta kvadratmetoden
19. Jupyter Notebook Cheat Sheet
20. Grunderna i Python
21. Pythonmönsterprogram
22. Generatorer i Python
23. Python Decorator
24. Python Spyder IDE
25. Mobila tillämpningar med hjälp av Kivy i Python
26. De tio bästa böckerna för att lära sig & öva Python
27. Robotramverk med Python
28. Ormspel i Python med PyGame
29. Django-intervjufrågor och svar
30. Topp 10 Pythonprogram
31. Hashtabeller och Hashmaps i Python
32. Python 3.8
33. Stödvektormaskin
34. Handledning i Python