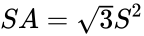Para la revista académica, véase Tetrahedron (journal).
| Tetraedro regular | |
|---|---|
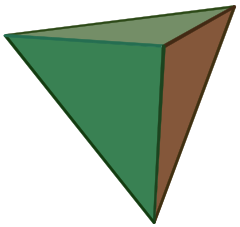 (Pulse aquí para ver el modelo giratorio) |
|
| Tipo | Sólido platónico |
| Elementos | F = 4, E = 6 V = 4 (χ = 2) |
| Caras por lados | 4{3} |
| Símbolo de Schläfli | {3,3} y s{2,2} |
| Símbolo de Wythoff | 3 | 2 3 | 2 2 |
| Anillo de Coxeter-Dynkin | |
| Simetría | Td o (*332) |
| U01, C15, W1 | |
| Propiedades | Deltaedro convexo regular |
| Ángulo diédrico | 70.528779° = arccos(1/3) |
 3,3.3 (Figura de vértice) |
 Autodual (poliedro dual) |
 Neto |
|
Un tetraedro (plural: tetraedros) es un poliedro compuesto por cuatro caras triangulares, tres de las cuales se encuentran en cada vértice. Un tetraedro regular es aquel en el que los cuatro triángulos son regulares, o «equiláteros», y es uno de los sólidos platónicos.
El tetraedro es un tipo de pirámide, que es un poliedro con una base poligonal plana y caras triangulares que conectan la base con un punto común. En el caso de un tetraedro la base es un triángulo (cualquiera de las cuatro caras puede considerarse la base), por lo que un tetraedro también se conoce como pirámide triangular o Deltaedro Digonal.
Fórmulas para el tetraedro regular
El volumen es {displaystyle V={frac {{3}}{12}}S^{3}
La superficie es
Template:Commonscat
- F. M. Jackson y Weisstein, Eric W., «Tetrahedron» de MathWorld.
- Weisstein, Eric W., «Tetrahedron» de MathWorld.
- Weisstein, Eric W., «Tetrahedron» de MathWorld.
- Los Poliedros Uniformes
- Tetrahedron: Interactive Polyhedron Model
- K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
- Fórmula de Piero della Francesca para el volumen del tetraedro en MathPages
- Modelos gratuitos en papel de un tetraedro y muchos otros poliedros
- Un asombroso, Space Filling, Non-regular Tetrahedron que también incluye una descripción de un «anillo giratorio de tetraedros», también conocido como calidociclo.
- Red de núcleos de tetraedros Aplicación de una estructura tetraédrica para crear una red de datos de malla parcial resistente
- Fórmulas exactas explícitas para el tensor de inercia de un tetraedro arbitrario en términos de sus coordenadas de vértice
- El tensor de inercia de un tetraedro
.