Introducción
Las transformaciones de coordenadas no son lo suficientemente intuitivas en 2D, y son dolorosas en 3D. Esta página las aborda en el siguiente orden: (i) vectores en 2D, (ii) tensores en 2D, (iii) vectores en 3D, (iv) tensores en 3D, y finalmente (v) transformaciones tensoriales de 4º rango.
Un aspecto importante de las transformaciones de coordenadas es la evaluación de la matriz de transformación, especialmente en 3D. Es muy importante reconocer que todas las transformaciones de coordenadas en esta página son rotaciones del sistema de coordenadas, mientras que el objeto en sí permanece fijo. El «objeto» puede ser un vector como la fuerza o la velocidad, o un tensor como la tensión o la deformación en un componente. Las rotaciones de objetos se tratan en secciones posteriores.
Transformaciones de coordenadas de vectores en 2D
La patata académica proporciona un excelente ejemplo de cómo se aplican las transformaciones de coordenadas a los vectores, a la vez que subraya que es el sistema de coordenadas el que gira y no el vector… o la patata.
La patata de la izquierda tiene un vector. Pero sin un sistema de coordenadas, no hay manera de describir el vector.Así que se ha añadido un sistema de coordenadas a la patata como se muestra a la derecha, lo que permite describir ahora el vector como \({\bf v} = 2{\bf i} + 9{\bf j}\).

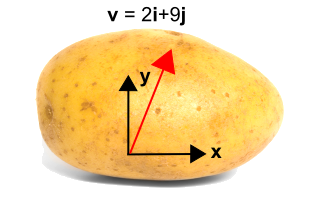
Así que ahora introducimos un sistema de coordenadas rotado que se muestra en azul a continuación, usando\\N(x’\\N) y \N(y’\N). El nuevo sistema está girado en sentido contrario a las agujas del reloj por un ángulo, \(\theta\), desde el sistema de coordenadas inicial. Nótese que el vector en sí no cambia en absoluto. Sigue siendo el mismo vector que antes. Pero se describe con valores numéricos diferentes en el nuevo sistema de coordenadas. En este caso, el vector es más paralelo al nuevo eje \ (x’\) que al eje \ (y’\), por lo que la componente \ (i’}) será mayor que la componente \ (j’}). La transformación se da debajo de la figura.
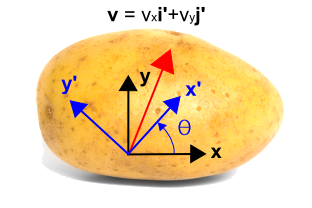
\\N-esto se puede ver observando queEstos cuatro factores constituyen los cuatro términos de las ecuaciones de transformación. Se comprueban fácilmente fijando \(\theta = 0^\c \) y \(\theta = 90^\c \). Cuando \(\theta = 0^\c\), entonces \(v’_x = v_x\) y \(v’_y = v_y\). Cuando \(\theta = 90^\c\), entonces \(v’_x = v_y\) y \(v’_y = -v_x\).
Matriz de transformación
Resulta más cómodo escribir (y trabajar con) las ecuaciones de transformación mediante matrices.
{Izquierda{{matriz{v_x{v_y}} \Los términos de la matriz están en la diagonal, mientras que los términos de la matriz están fuera de la diagonal. El único problema potencial es recordar qué término \(\sin \theta\) tiene el signo menos. Siempre es el término inferior izquierdo.
La ecuación anterior se escribe en notación matricial como
\
donde \({\bf Q}\) es la letra habitual elegida para la matriz de transformación.

Matrices de transformación vs. Matrices de rotación
Si este tema no fuera ya lo suficientemente difícil, muchos libros y páginas web aumentan la confusión al no aclarar qué es fijo y qué es de rotación. En esta página y en la siguiente, es el sistema de coordenadas el que gira mientras el objeto permanece fijo, por lo que el término matriz de transformación se utiliza aquí para enfatizarlo.
Sin embargo, más adelante abordaremos situaciones en las que el objeto gira mientras el sistema de coordenadas permanece fijo. En este caso, se utilizará el término matriz de rotación para enfatizar que el objeto está girando.
Mucha confusión surge del sorprendente hecho de que cada matriz (de transformación y de rotación) es simplemente la transposición de la otra. Así que se parecen mucho. En los problemas bidimensionales, la única diferencia práctica es si el signo menos delante de \(\sin \theta\) está en el término \(q_{12}\), o en el término \(q_{21}\).
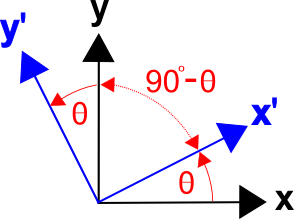
Existe un método general para formular matrices de transformación basadas en los cosenos de los ángulos entre los ejes de los dos sistemas de coordenadas, es decir, cosenos de dirección. (Esto también se aplica a las transformaciones tridimensionales.)La matriz de transformación puede escribirse como
\\Ndonde \((x’,x)\Nrepresenta el ángulo entre los ejes \N(x’\) y \N(x\), \N((x’,y)\Nes el ángulo entre los ejes \N(x’\) y \N(y\), etc.
El ángulo entre \(x’\) y \(y\) es \((90^\c – \theta)\), y \(\cos(x’,y) = \cos(90^\c – \theta) = \sin \theta\).
Así mismo, el ángulo entre \(y’\) y \(x\) es \((90^\circ + \theta)\), y \(\cos(y’,x) = \cos(90^\circ + \theta) = -\sin \theta).
Notación tensorial
La transformada de coordenadas se escribe en notación tensorial como
\
donde \(\lambda_{ij}\) es la matriz de transformación \({\bf Q}\). (No sé por qué se utiliza \({\bf Q}\) en notación matricial, pero \(\lambda_{ij}\), no \(q_{ij}\), se utiliza en notación tensorial). \(\lambda_{ij}\) se define como
\
Por ejemplo, si \(i = 1\) y \(j = 2\), entonces
\
(\lambda_{ij}\) es el coseno de la dirección del ángulo entre el eje \(x’_i\) y el eje \(x_j\). Una vez más, esto es igualmente aplicable a las transformaciones en 3-D también.
Transformaciones de coordenadas en 2-D de los tensores
Esta sección presentará el qué y el cómo de las transformaciones tensoriales.El por qué tendrá que esperar hasta más tarde.
Las transformaciones de coordenadas de los tensores de 2º rango implican la misma matriz \({\bf Q}\} que las transformaciones vectoriales. Una transformación del tensor de tensiones, \(\boldsymbol{\sigma}\), desde el sistema de coordenadas \(x-y\) de referencia a \(\boldsymbol{\sigma’}) en un nuevo sistema \(x’-y’\) se hace como sigue.
\NSi se escriben las matrices explícitamente se obtiene
\Nque el tensor de tensiones es siempre simétrico, incluso después de las transformaciones.)
Multiplicando las matrices se obtiene
\N
Estas tres ecuaciones son exactamente la transformación bidimensional de un tensor de tensiones resultante de sumar fuerzas en un elemento diferencial e imponer el equilibrio. Esto también está representado por el círculo de Mohr.
Notación tensorial
La transformación de coordenadas se escribe en notación tensorial como
Como es habitual, la notación tensorial proporciona una visión adicional del proceso. Esta vez, la información proviene de los subíndices de las lambdas. Cada lambda efectivamente pares hasta un subíndice en \ ~ (\boldsymbol ‘sigma’) con uno en \ ~ (\boldsymbol ‘sigma’).Esto es cierto independientemente del rango del tensor.
Transformaciones de coordenadas en 3-D de los vectores
Muchas de las ecuaciones generales usadas en las transformaciones en 2-D son también aplicables en 3-D.Los ejemplos incluyen
\
Sólo que ahora los detalles son diferentes. Los vectores tienen componentes z y las matrices de transformación son de 3×3 en lugar de 2×2.
[
[
[
[izquierda] {matriz { v_x \_y \ v_z }
Transformaciones de coordenadas de tensores en 3-D
Una vez más, las reglas no cambian, sólo los detalles lo hacen.
Escribiendo las matrices explícitamente se obtiene
\a = \a izquierda\a izquierda]
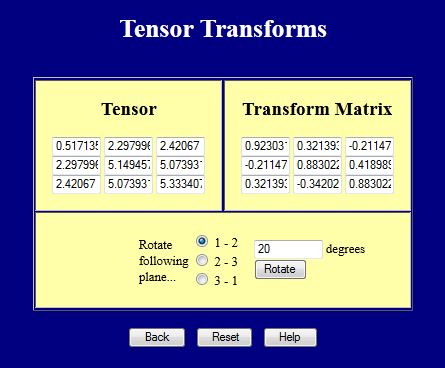
Esta página web realiza transformaciones de coordenadas en tensores en 3-D. Pruébalo.
Transformaciones de coordenadas de tensores de 4º rango
Veremos en la sección sobre la Ley de Hooke que el tensor de rigidez es de 4º rango, es decir, 3x3x3x3 (no 4×4). Se escribe como \(C_{kl}\ porque relaciona cualquier componente de deformación, \(\epsilon_{kl}\), con cualquier componente de tensión, \(\sigma_{ij}\), es decir \La ley de transformación de coordenadas para el tensor de rigidez de cuarto rango se escribe fácilmente en notación tensorial como
La ecuación tensorial indica cómo escribir la transformación en notación matricial.
\
Resumen
La transformación de coordenadas de un vector en notación matricial y tensorial es
\
La transformación de coordenadas de un tensor en notación matricial y tensorial es
\
Nota que \({\bf Q}\) y \(\lambda_{ij}\) son la misma matriz de transformación.
En 2-D, \({\bf Q}\) y \(\lambda_{ij}\) se definen como
]
que es un caso especial de la forma más general en 3-D
]