Střídavý proud se tak jmenuje proto, že proud střídavě přechází mezi dvěma polaritami. Jinými slovy, proud (a tedy i napětí) je funkcí času. Tím se zásadně liší od stejnosměrného proudu, který má pevnou polaritu a je obecně konstantní v čase. Například laboratorní zdroj stejnosměrného napětí v ideálním případě udržuje na svých svorkách nastavené napětí a v čase se nemění. Naproti tomu, jak střídavý proud kmitá v čase sem a tam, může jeho tvar vykazovat široké variace, od jednoduchých, pravidelných průběhů laboratorních standardů, jako jsou sinusovky, trojúhelníky a čtverce, až po mnohem složitější a zvlněné průběhy, které vytvářejí hudební nástroje a lidský hlas.
Sinusovka je nejjednodušší vlna, kterou lze vytvořit. Představuje pohyb jednoduchého vektoru otáčejícího se konstantní rychlostí, například vertikální posun vteřinové ručičky hodin. Příklad je na obrázku \(\PageIndex{1}\). Na vodorovné ose je zobrazen čas. Zvětšuje se, jak se pohybujeme zleva doprava (tj. pokud se bod A nachází napravo od bodu B, pak bod A nastane v čase později než bod B). Svislá osa je zde znázorněna obecně jako procento z maxima, ale obvykle by se jednalo o měření napětí, proudu, akustického tlaku nebo podobně.
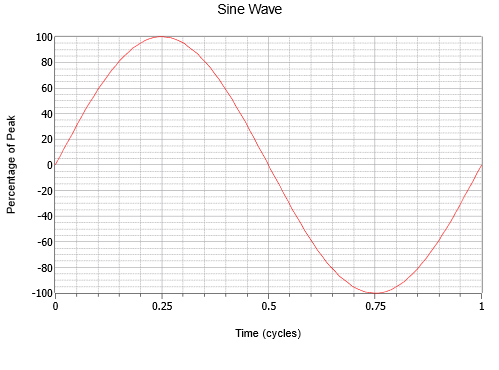
Obrázek \(\PageIndex{1}\):
Všimněte si plynulého kolísání, které začíná na nule, stoupá do kladného vrcholu v jedné čtvrtině cesty, v polovině cesty klesá zpět na nulu, pokračuje do záporného vrcholu ve třech čtvrtinách cesty a pak opět stoupá tam, kde začalo. Tento proces se pak opakuje. Každé opakování se označuje jako cyklus. Na obrázku \(\PageIndex{1}\) je zobrazen jeden úplný cyklus.
Sinusové vlny vykazují symetrii čtvrtvln. To znamená, že každá čtvrtina (v čase) vlny je totožná s jakoukoli jinou, pokud ji jednoduše otočíte kolem vodorovné osy a/nebo otočíte svisle kolem jejího vrcholu. Doba potřebná k dokončení jednoho cyklu se nazývá perioda a označuje se symbolem \(T\) (pro Čas). Reciproční hodnota periody je frekvence, \(f\).
\
Frekvence udává, kolik cyklů existuje za jednu sekundu. Na počest jednoho z badatelů 19. století v tomto oboru používáme místo označení jednotky „cykly za sekundu“ označení Hertz, pojmenované podle Heinricha Hertze a zkrácené Hz. Na obrázku \(\PageIndex{2}\) jsou zobrazeny tři sinusové vlny s různými frekvencemi; počáteční vlna (zelená), vlna s dvojnásobnou frekvencí (modrá) a třetí s poloviční frekvencí nebo dvojnásobnou periodou (červená).
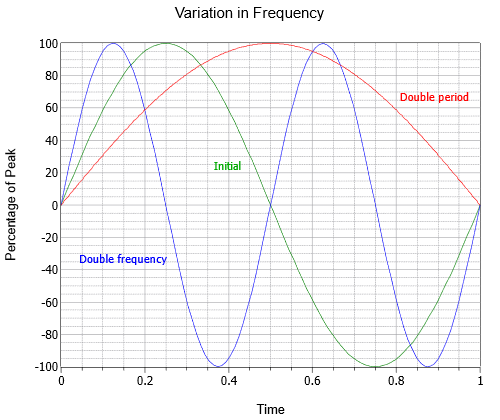
Obrázek \(\PageIndex{2}\):
Amplitudu (vertikální) vlny lze vyjádřit jako vrcholovou veličinu, což je změna od střední nulové čáry až po nejpozitivnější hodnotu. Amplitudu lze také vyjádřit jako hodnotu od vrcholu k vrcholu; vzdálenost od nejnegativnější hodnoty k nejpozitivnější. U sinusové vlny to bude vždy dvojnásobek vrcholové hodnoty, i když to nemusí platit pro jiné vlny, které mohou být asymetrické. Na obrázku \(\PageIndex{3}\) je znázorněna řada tří sinusových vln s různými amplitudami. Vedle původní (zelené) jsou uvedeny verze s dvojnásobnou amplitudou (modrá) a poloviční amplitudou (červená).
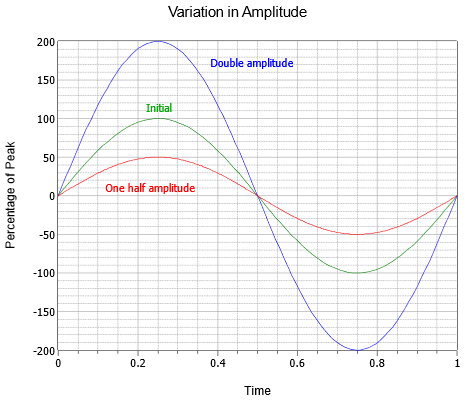
Obrázek \(\PageIndex{3}\):
Kombinací těchto parametrů uvažujte průběh napětí zobrazený na obrázku \(\PageIndex{4}\). Zde vidíme dva cykly průběhu střídavého napětí.
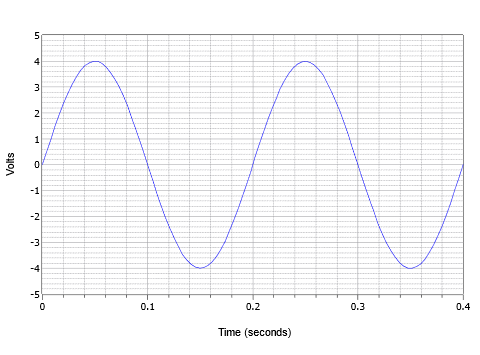
Obrázek \(\PageIndex{4}\):
Příklad základního sinusového průběhu.
Vrcholová hodnota je 4 volty a hodnota od špičky do špičky je 8 voltů (obvykle zkráceně „8 V pp“). Perioda jednoho cyklu je 0,2 sekundy nebo \(T = 200\) milisekund. Dále je to frekvence \(f = 1/200\) milisekund, neboli 5 Hz (5 cyklů za jednu sekundu).
Střídavé průběhy mohou být také kombinovány se stejnosměrným posunem. Přidání kladné stejnosměrné úrovně posune vlnu vertikálně nahoru, zatímco záporná stejnosměrná úroveň posune vlnu vertikálně dolů. Tím se nemění frekvence ani střídavá část amplitudy (ačkoli absolutní špičky by se posunuly o hodnotu stejnosměrného proudu). Obrázek \(\PageIndex{5}\) ukazuje vliv různých stejnosměrných posunů. Nad původní vlnou (zelená) je jinak identická vlna s kladným stejnosměrným posunem rovným 20 % původní vrcholové hodnoty (modrá). Pod původní vlnou je třetí vlna (červená), která vykazuje záporný stejnosměrný posun rovnající se polovině vrcholové hodnoty původní vlny.
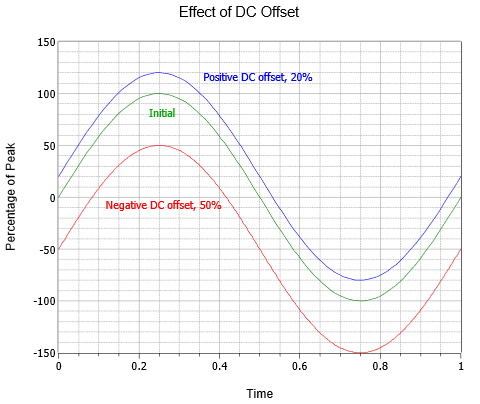
Obrázek \(\PageIndex{5}\):
Dále je možné, aby byla sinusová vlna časově posunuta oproti jiné sinusové vlně nebo referenci. I když je možné tento posun uvést jako absolutní čas, častěji se to dělá jako fázový posun, tj. čas vyjádřený jako část periody ve stupních. Pokud například jedna sinusoida předbíhá druhou o čtvrtinu periody, říká se, že vede o 90\(^{\circ}\) (tj. 1/4 360\(^{\circ}\)). Pokud je pozadu o ½ periody, říká se, že je pozadu o 180\(^{\circ}\) (tj. později v čase o 1/2 cyklu). Jiný způsob vyjádření je, že vedoucí průběhy začínají v čase dříve, a proto jsou vykresleny vlevo od reference, zatímco opožděné průběhy začínají v čase později a jsou vykresleny vpravo.
Obrázek \(\PageIndex{6}\) znázorňuje vliv fázového posunu. Všimněte si, že v tomto grafu byl \(t = 0\) posunut do středu vodorovné osy. Prostřední křivka je počáteční nebo referenční vlna (zelená). Vlevo (červená) je vlna, která vede počáteční vlnu o jednu osminu cyklu, neboli 45\(^{\circ}\). Vpravo (modrá) je vlna zaostávající o polovinu cyklu, tedy -22,5\(^{\circ}\).
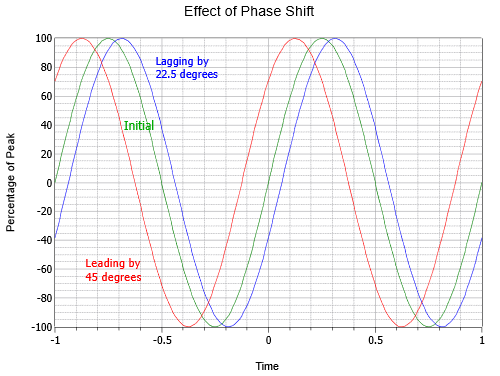
Obrázek \(\PageIndex{6}\): Změny fáze sinusové vlny.
Kombinace výše uvedených prvků nám umožňuje vytvořit obecný formát sinusové vlny (zobrazeno napětí):
\
Kde
\(v(t)\) je napětí v určitém čase \(t\),
\(V_{DC}\) je případný stejnosměrný offset,
\(V_{P}\) je špičková hodnota,
\(f\) je frekvence,
\(\theta\) je fázový posun (+, pokud vede a je nakreslen vlevo, -, pokud zaostává a je nakreslen vpravo).
Pro rychlý a praktický příklad má průběh zobrazený na obrázku \(\PageIndex{4}\) amplitudu 4 volty ve špičce, frekvenci 5 Hz a žádný stejnosměrný posun nebo fázový posun. Jeho vyjádření je tedy \(v(t) = 4 \sin (2 \pi 5 t)\)
Pro výpočet fázového posunu nejprve určete časový rozdíl mezi průběhem a referencí, který nazveme \(\Delta t\). Referencí může být pevný časový bod (např. \(t = 0\)) nebo jiný průběh. Obecně je snadné změřit rozdíl při průchodu nulou za předpokladu, že neexistuje stejnosměrný offset. Pokud offset existuje, proveďte měření v místě, kam byl posunut průchod nulou (tj. na úrovni stejnosměrného offsetu). Po zjištění rozdílu jej vydělte periodou, abyste posun vyjádřili jako zlomek periody. Protože jeden cyklus představuje jedno otočení vektoru neboli 360 stupňů, jednoduše vynásobte zlomek 360 stupni, abyste zjistili fázový posun ve stupních. Vyjádřeno vzorcem:
\
Pamatujte, že pokud je vlna posunuta doleva, pak je vedoucí a kladná, zatímco posun doprava je zpožděný nebo opožděný v čase, a tedy záporný.
Příklad \(\PageIndex{1}\)
Napište výraz pro průběh zobrazený na obrázku \(\PageIndex{7}\).
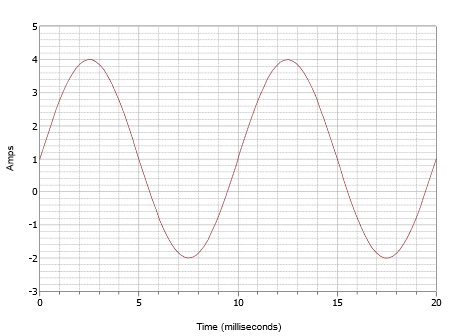
Obrázek \(\PageIndex{7}\):
Tento průběh může na první pohled vypadat jako průběh na obrázku \(\PageIndex{4}\), ale nenechte se zmást. Především se liší časové měřítko. U tohoto průběhu se jeden cyklus dokončí za 10 milisekund. Proto je frekvence
\
\
\
\
Druhým problémem je stejnosměrný offset. Všimněte si, že kladná špička se vyskytuje při 4 ampérech, zatímco záporná při -2 ampérech. To znamená, že hodnota špička-špička je 6 ampér. Bez offsetu by kladná špička byla při 3 ampérech, proto je zde stejnosměrný offset +1 ampér. Vertikální střed křivky je posunut nahoru z 0 ampérů na +1 ampér. Tento bod je v bodě t = 0, proto nedochází k žádnému fázovému posunu. Výsledný výraz je:
\
Příklad \(\PageIndex{2}\)
Napište výraz pro průběh zobrazený na obrázku \(\PageIndex{8}\).
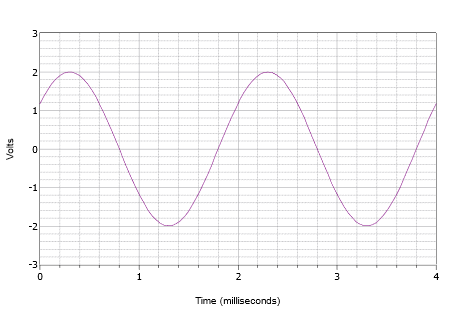
Obrázek \(\PageIndex{8}\):
Předně, kladná špička je 2 volty a hodnota špička-špička je 4 volty. Proto zde není žádný stejnosměrný offset. Vertikální střed vlny nezačíná v bodě \(t = 0\), proto musí dojít k fázovému posunu. Hodnota při \(t = 0\) je 1,2 voltu. Vlna dosáhne stejné amplitudy v \(t = 2\) milisekundy a začne opakovat další cyklus. Z toho vyplývá, že perioda musí být 2 milisekundy. Frekvence je reciproká této hodnoty, a tedy \(f = 500\) Hz.
Křivka je posunuta doleva, což znamená kladný nebo vedoucí fázový posun. Prozkoumáme-li druhý cyklus, vidíme, že na nulu se dostane v čase 1,8 milisekundy. Posun je tedy 0,2 milisekundy. Vyjádřeno ve stupních je to:
\
\
\
Konečný výraz je:
\
Příklad \(\PageIndex{3}\)
Nakreslete průběh odpovídající následujícímu výrazu.
\
Nejprve si všimněte, že posunutí o -3 volty sráží kladný pík z 5 voltů na 2 volty a záporný pík z -5 voltů na -8 voltů. Frekvence 40 kHz diktuje periodu:
\
\
\
Fázový posun -72\(^{\circ}\) představuje 72/360, neboli 0,2 cyklu. To odpovídá časovému zpoždění (posunutému doprava, protože je záporné) 0,2 krát 25 \(\mu\)s, neboli 5 \(\mu\)s.
Zpočátku je často lepší sestrojit graf pomocí řady diskrétních kroků, než se snažit nakreslit jej celý najednou. Nejprve nakreslete sinusovku se špičkovou amplitudou 5 V a periodou 25 \(\mu\)s. Nyní posuňte průběh o 3 volty dolů, aby kladná špička byla pouze 2 volty a záporná špička -8 voltů. Nakonec posuňte nově posunutý průběh doprava o 5 \(\mu\)s. Výsledek je zobrazen na obrázku \(\PageIndex{9}\).
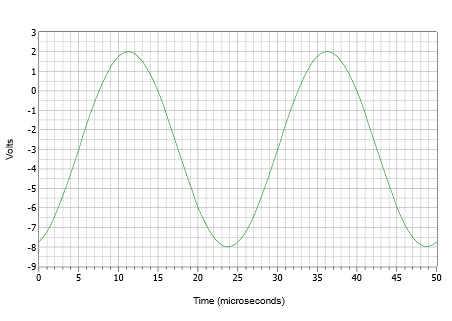
Obrázek \(\PageIndex{9}\):
1.2.1: Průběh pro příklad \(\PageIndex{3}\): Laboratorní měření
V laboratoři se ke generování sinusových a jiných tvarů vln používá generátor funkcí. Tato zařízení umožní přesnou kontrolu amplitudy i frekvence vlny spolu s případným přidáním stejnosměrného offsetu. Příklad je uveden na obrázku \(\PageIndex{10}\). Odpovídajícím měřicím přístrojem je osciloskop nebo zkráceně jen scope.

Obrázek \(\PageIndex{10}\):
Osciloskop je pravděpodobně nejužitečnější a nejuniverzálnější měřicí zařízení v laboratoři. Obvykle jsou vybaveny dvěma nebo čtyřmi vstupními kanály, i když jich může být i více. Každý vstupní kanál má vlastní nastavení citlivosti a všechny kanály mají společnou časovou referenci. Displej vykresluje průběhy stejným způsobem jako na obrázcích \(\PageIndex{1}\) – \(\PageIndex{9}\). Také mohou vykreslovat jedno napětí vůči druhému (režim X – Y). Moderní osciloskopy mají další funkce, jako je automatické měření frekvence, amplitudy, fázového posunu atd., měření pomocí kurzoru a možnost ukládat obrázky displeje jako grafické soubory. Příklad čtyřkanálového digitálního osciloskopu je uveden na obrázku \(\PageIndex{11}\).

Obrázek \(\PageIndex{11}\):
1.2.2: Symboly pro schémata
Co se týče schémat, symboly pro zdroje střídavého napětí a proudu jsou uvedeny na obrázku \(\PageIndex{12}\). Označení polarity a směru není absolutní; jde přece o zdroje střídavého proudu, jejichž polarita a směry se převracejí tam a zpět. Značky se místo toho používají k určení časové reference, zejména v obvodech využívajících více zdrojů.
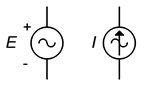
Obrázek \(\PageIndex{12}\):
Je třeba si uvědomit, že negace zdroje je totéž jako převrácení jeho polarity. To platilo pro zdroje stejnosměrného proudu a platí to i pro zdroje střídavého proudu. To je znázorněno na obrázku \(\PageIndex{13}\). Někdy převrácení nebo negace zdroje učiní analýzu o něco zřejmější nebo snadněji vizualizovatelnou.
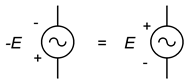
Obrázek \(\PageIndex{13}\):
Příklad \(\PageIndex{4}\)
Předpokládejme, že osciloskop zobrazí dvě vlny, jak je znázorněno na obrázku \(\PageIndex{14}\). Určete fázový posun menší vlny se špičkou 20 V (modrá) vůči větší vlně se špičkou 25 V (červená).
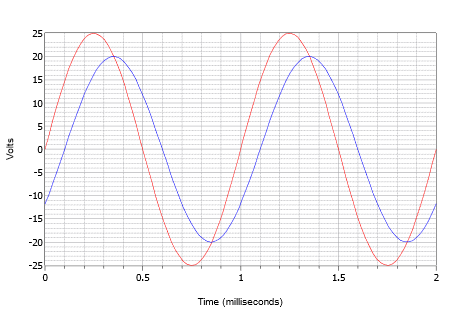
Obrázek \(\PageIndex{14}\):
Nejprve si všimněte, že ani jedna z vln nevykazuje stejnosměrný posun. Pokud by jedna nebo obě měly posun, musela by být vlna(y) vertikálně posunuta(y) tak, aby jejich normální body průsečíku nul byly na stejné úrovni. Při měření obou vln se zjistí, že perioda je 1 milisekunda. Časový posun lze nejsnáze zjistit na kterémkoli z průsečíků nul (na výběr jsou čtyři místa). Zpoždění je jedna malá odchylka, tedy 0,1 milisekundy, přičemž menší vlna je časově zpožděná neboli zaostává za větší vlnou. To značí záporný fázový posun.
\
\
\
1.2.3: Sinusy a kosinusy
Existuje několik specifických fázových posunů, které stojí za bližší pozornost. Pokud je sinusovka invertovaná, tedy převrácená vzhůru nohama, je k nerozeznání od sinusovky, která byla posunuta o +180 nebo -180 stupňů. Jinými slovy, takovou vlnu lze zapsat třemi různými způsoby: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\) nebo \(\sin (2 \pi ft + 180^{\circ})\). Dále, pokud je sinusová vlna posunuta o +90 stupňů (tj. dopředu a doleva), lze ji také označit jako kosinusovou vlnu. Tedy \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). A konečně, pokud je sinusová vlna posunuta o -90 stupňů (tj. zpožděná a doprava), lze ji označit jako zápornou nebo obrácenou kosinusovou vlnu. Tedy \(\sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). Vztahy těchto čtyř vln jsou znázorněny na obrázku \(\PageIndex{15}\).
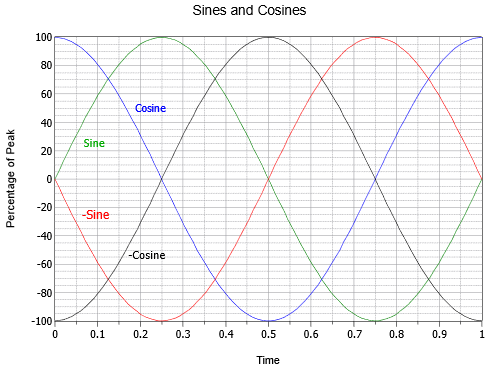
Obrázek \(\PageIndex{15}\): Časové vztahy mezi sinusy a kosinusy.
Je třeba také poznamenat, že kosinusová vlna představuje první derivaci neboli sklon sinusové vlny. Jak si možná vzpomínáte z jiných studií, sklon neboli „strmost“ přímky je poměr vertikální změny k horizontální změně, někdy se nazývá „nárůst nad dráhou“. Pro napětí by to byla změna napětí nad změnou času, neboli \(\Delta V/ \Delta t\). Pro hladkou, spojitě se měnící křivku, jako je sinusovka, je sklon v daném bodě správně definován jako první derivace, neboli v tomto případě \(dv/dt\). Chcete-li si vizuálně ověřit, že to platí, všimněte si, že nejstrmější část sinusoidy (zelená) je v místě, kde prochází nulovou amplitudou. Jakmile překročí nulu při kladném pohybu (v bodě \(t = 0\) nebo \(t = 1\) na obrázku \(\PageIndex{15}\)), kosinus (modrá) je na svém kladném vrcholu. Když sinus překročí nulu při záporném pohybu (v \(t = 0,5\)), kosinus je na svém záporném vrcholu. Dále je sinusovka plochá s nulovým sklonem v kladném a záporném vrcholu (v \(t = 0,25\) a \(t = 0,75\)) a v těchto okamžicích je také amplituda kosinusu nulová. Platí také, že sinusovka je sklonem záporné kosinusovky, záporná kosinusovka je sklonem záporné sinusovky a záporná sinusovka je sklonem kosinusovky. Přejdeme-li opačným směrem, můžeme říci, že antiderivát (neurčitý integrál) kosinové vlny je sinusová vlna, integrál sinusové vlny je záporná kosinová vlna atd. Tyto vztahy se ukáží jako nejužitečnější, až se budeme věnovat odezvě kondenzátorů a cívek v obvodech střídavého proudu.
1.2.4: RMS – měření střední kvadratické hodnoty
Společně se špičkou a špičkou k špičce lze amplitudu udávat jako střední kvadratickou hodnotu (RMS – Root Mean Square). Ve skutečnosti, pokud není zadána špička nebo špička-špička, předpokládá se, že měření je RMS. RMS je speciální výpočet, který se používá pro zjištění ekvivalentního stejnosměrného výkonu (velmi časté například u audio zesilovačů). Jinými slovy, pokud nás zajímá zjištění výkonu v rezistoru, musí být výpočet proveden pomocí efektivních hodnot napětí nebo proudu, nikoliv špičkových hodnot nebo hodnot špička-špička. Pokud tak neučiníme, dostaneme chybné výkony. To platí bez ohledu na tvar vlny; ať už se jedná o sinusovku, trojúhelník nebo komplexní vlny hudebních signálů. Pokud je napětí zadáno jako efektivní hodnota, lze s ním pro výpočet výkonu zacházet stejně jako s ekvivalentně velkým stejnosměrným napětím. Například sinusové napětí 1 V RMS způsobí stejný rozptyl výkonu a zahřívání v daném rezistoru jako stejnosměrné napětí 1 V. Z tohoto důvodu se RMS někdy označuje jako efektivní hodnota (tj. efektivní hodnota stejnosměrného proudu).
Název root-mean-square popisuje proces určení efektivní hodnoty. Nejprve si připomeňme, že výkon je úměrný kvadrátu napětí nebo proudu. Naším prvním krokem tedy bude kvadratizace vstupního průběhu. Průběh je samozřejmě funkcí času a jeho kvadrát poskytne nějaký nový tvar. V tomto okamžiku musíme najít střední hodnotu tohoto nového tvaru. Důvod je jednoduchý, avšak ne vždy zřejmý. Elektrické a elektronické součástky mají hmotnost, a proto se nezahřívají ani nechladí okamžitě. Vykazují tepelnou časovou konstantu. Proto reagují na průměrný příkon v průběhu času. I když bychom mohli vypočítat nějakým způsobem „okamžitý špičkový výkon“ v určitém časovém okamžiku, nepředstavuje to ekvivalentní stejnosměrný výkon. Jakmile získáme střední hodnotu tohoto kvadratického průběhu, odpovídající stejnosměrná hodnota je pouze odmocninou ze střední hodnoty. Výsledkem je zlomková hodnota mezi nulou a jedničkou, která se používá jako škálovací faktor pro přeměnu špičkové hodnoty na efektivní hodnotu. Tato hodnota bude jedinečná pro konkrétní tvar vlny. To znamená, že všechny sinusovky (bez ohledu na fázi) mají stejný faktor, všechny pravidelné trojúhelníkové vlny mají stejný faktor atd. Protože se většinou zabýváme sinusovkami, podívejme se blíže na určení jejich efektivního činitele.
Začneme základním výrazem pro sinusovku bez stejnosměrného posunu nebo fázového posunu a s amplitudou rovnou jedné:
\
Prvním krokem je kvadratizace tohoto průběhu. Užitečná trigonometrická identita je
\
Při jejím použití na naši vlnu získáme:
\
Tento výraz popisuje převrácenou kosinusovou vlnu s dvojnásobkem původní frekvence a polovinou původní amplitudy, která jede na stejnosměrném posunu rovném její vrcholové hodnotě. Jinými slovy, záporný vrchol kosinusu je na nule a kladný vrchol je na 1. Dalším krokem je nalezení průměrné nebo střední hodnoty tohoto mezivýsledku. Střední hodnota je rovna posunu 0,5. To si lze představit jako oblast nad offsetem, která dokonale vyplňuje „propad“ pod offsetem. Posledním krokem je druhá odmocnina z průměrné hodnoty. Druhá odmocnina z 0,5 se rovná jedné odmocnině ze dvou, tedy přibližně 0,707. RMS hodnota je tedy 0,707 krát vrcholová hodnota. Alternativně můžete špičku vydělit druhou odmocninou ze dvou, tedy přibližně 1,414. Tento postup je graficky znázorněn na obrázku \(\PageIndex{16}\).
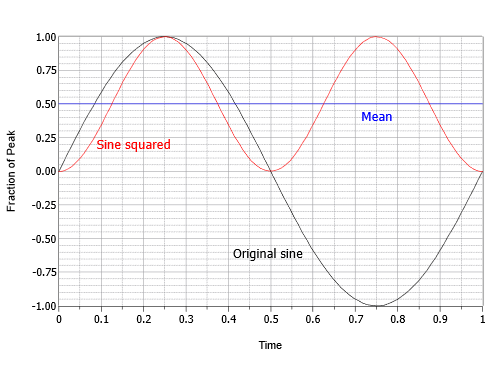
Obrázek \(\PageIndex{16}\):
Při sčítání sinusových vln je efektivní hodnota vždy vrcholová hodnota krát 0,707. Mohli bychom také říci, že efektivní hodnota libovolné sinusovky je její vrcholová hodnota dělená přibližně 1,414. Tyto poměry by opět nemusely nutně platit pro nesinusové vlny. Podrobnosti týkající se dalších běžných tvarů najdete v příloze C. Konečně poměr vrcholové hodnoty k efektivní hodnotě se nazývá hřebenový poměr. Ten má u sinusových vln pevnou hodnotu (opět přibližně 1,414), ale u některých druhů zvukových signálů může být vyšší než 10:1.
1.2.5: Vlnová délka
Další zajímavou položkou je rychlost šíření vlny. Ta se značně liší. V případě světla ve vakuu (nebo v blízkém přiblížení elektrického proudu ve vodiči) je rychlost asi 3E8 metrů za sekundu (tj. 300 000 km/s) nebo asi 186 000 mil za sekundu.
Při dané rychlosti a periodě si můžeme představit, jak daleko od sebe jsou vrcholy vlny. Tato vzdálenost se nazývá vlnová délka a označuje se řeckým písmenem lambda \(\lambda\). Vlnová délka se rovná rychlosti dělené frekvencí, \(\lambda = v/f\). Pro reproduktor produkující sinusový zvuk o frekvenci 100 Hz je tedy rychlost zvuku ve vzduchu 344 m/s, tedy \(\lambda = 344 m/s \, / \, 100\) Hz, neboli 3,44 metru (něco přes 11 stop). Všimněte si, že čím vyšší je frekvence, tím kratší je vlnová délka. Všimněte si také, že čím vyšší je rychlost, tím delší je vlnová délka. Výpočty vlnových délek mají význam zejména v oblasti telekomunikací a akustiky.
.