
Matematika se zabývá obrovským množstvím pojmů, které jsou velmi důležité, ale zároveň složité a časově náročné. Python však poskytuje plnohodnotnou knihovnu SciPy, která tento problém řeší za nás. V tomto výukovém kurzu SciPy se dozvíte, jak tuto knihovnu využívat spolu s několika funkcemi a jejich příklady.
Předtím, než budete pokračovat, podívejte se na všechna témata probíraná v tomto článku:
- Co je SciPy?
- NumPy vs SciPy
- Podbalíčky v SciPy
- Základní funkce
- Speciální funkce
- Integrační funkce
- Optimalizační funkce
- Fouierovy transformační funkce
- Signálové funkce. Processing Functions
- Lineární algebra
- Sparse Eigenvalues
- Prostorové datové struktury a algoritmy
- Funkce pro zpracování vícerozměrného obrazu
- File IO
Takže začněme. 🙂
SciPy je open-source knihovna jazyka Python, která se používá k řešení vědeckých a matematických problémů. Je postavena na rozšíření NumPy a umožňuje uživateli manipulovat s daty a vizualizovat je pomocí široké škály vysokoúrovňových příkazů. Jak již bylo zmíněno, SciPy staví na NumPy, a proto pokud importujete SciPy, není třeba importovat NumPy.
NumPy vs SciPy
Obě knihovny NumPy a SciPy jsou knihovny Pythonu používané pro používané matematické a numerické analýzy. NumPy obsahuje datová pole a základní operace, jako je třídění, indexování atd. zatímco SciPy se skládá z veškerého numerického kódu. Ačkoli NumPy poskytuje řadu funkcí, které mohou pomoci řešit lineární algebru, Fourierovy transformace atd., SciPy je knihovna, která ve skutečnosti obsahuje plnohodnotné verze těchto funkcí spolu s mnoha dalšími. Pokud však provádíte vědeckou analýzu pomocí jazyka Python, musíte si nainstalovat jak NumPy, tak SciPy, protože SciPy staví na NumPy.
Podbalíčky v SciPy:
SciPy má řadu podbalíčků pro různé vědecké výpočty, které jsou uvedeny v následující tabulce:

Pro podrobný popis však můžete sledovat oficiální dokumentaci.
Tyto balíčky je třeba před jejich použitím výhradně importovat. Například:
from scipy import cluster
Než se na jednotlivé funkce podíváme podrobněji, podívejme se nejprve na funkce, které jsou společné jak pro NumPy, tak pro SciPy.
Interakce s NumPy:
SciPy staví na NumPy, a proto můžete využívat samotné funkce NumPy pro práci s poli. Chcete-li se o těchto funkcích dozvědět více do hloubky, můžete jednoduše využít funkce help(), info() nebo source().
help():
Chcete-li získat informace o jakékoli funkci, můžete využít funkci help(). Tuto funkci lze použít dvěma způsoby:
- bez parametrů
- použitím parametrů
Tady je příklad, který ukazuje oba výše uvedené způsoby:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Při spuštění výše uvedeného kódu vrátí první funkce help() informace o podmodulu clusteru. Druhá metoda help() požádá uživatele o zadání názvu libovolného modulu, klíčového slova atd. pro které si uživatel přeje vyhledat informace. Chcete-li zastavit provádění této funkce, jednoduše zadejte ‚quit‘ a stiskněte enter.
info():
Tato funkce vrací informace o požadovaných funkcích, modulech atd.
scipy.info(cluster)
source():
Zdrojový kód se vrací pouze pro objekty napsané v jazyce Python. Tato funkce nevrací užitečné informace v případě, že jsou metody nebo objekty napsány v jiném jazyce, například v jazyce C. Nicméně v případě, že chcete tuto funkci využít, můžete tak učinit následujícím způsobem:
scipy.source(cluster)
Speciální funkce:
SciPy poskytuje řadu speciálních funkcí, které se používají v matematické fyzice, například eliptické, komfortní funkce, gama, beta atd. Pro vyhledání všech funkcí můžete využít funkci help(), jak bylo popsáno dříve.
Exponenciální a trigonometrické funkce:
Balík speciálních funkcí SciPy poskytuje řadu funkcí, pomocí kterých můžete najít exponenty a řešit trigonometrické úlohy.
Podívejte se na následující příklad:
PŘÍKLAD:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
VÝSLEDEK:
1000,0
8,0
1,0
0.7071067811865475
V balíčku speciálních funkcí SciPy se nachází mnoho dalších funkcí, které si můžete sami vyzkoušet.
Integrační funkce:
SciPy poskytuje řadu funkcí pro řešení integrálů. Od obyčejného diferenciálního integrátoru až po použití lichoběžníkových pravidel pro výpočet integrálů, SciPy je zásobárnou funkcí pro řešení všech typů integrálních úloh.
Obecná integrace:
SiPy poskytuje funkci s názvem quad pro výpočet integrálu funkce, která má jednu proměnnou. Limity mohou být ( ) pro označení nekonečných limit. Syntaxe funkce quad() je následující:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Zde bude funkce integrována mezi limity a a b (může být i nekonečná).
PŘÍKLAD:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
V uvedeném příkladu se funkce ‚a‘ vyhodnotí mezi limity 0, 1. Po provedení tohoto kódu se zobrazí následující výstup.
VÝSTUP:
(3,9086503371292665, 4,3394735994897923e-14)
Dvojná integrální funkce:
SciPy poskytuje funkci dblquad, kterou lze použít k výpočtu dvojných integrálů. Dvojný integrál, jak mnozí z nás vědí, se skládá ze dvou reálných proměnných. Funkce dblquad() přijme jako svůj parametr integrovanou funkci spolu s dalšími 4 proměnnými, které definují limity a funkce dy a dx.
PŘÍKLAD:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
VÝSLEDEK:
-1.33333333333335, 1.4802973661668755e-14)
SciPy poskytuje různé další funkce pro vyhodnocování trojných integrálů, n integrálů, Rombergových integrálů atd. které můžete dále podrobně prozkoumat. Chcete-li zjistit všechny podrobnosti o požadovaných funkcích, použijte funkci help.
Optimalizační funkce:
Scipy.optimize poskytuje řadu běžně používaných optimalizačních algoritmů, které si můžete prohlédnout pomocí funkce help.
Jedná se v podstatě o následující:
- Omezená a omezená minimalizace vícerozměrných skalárních funkcí, tj. minimalizace (např. BFGS, Newton Conjugate Gradient, Nelder_mead simplex atd.)
- Globální optimalizační rutiny (např. differential_evolution, dual_annealing atd.)
- Minimalizace nejmenších čtverců a fitování křivek (např. least_squares, curve_fit atd.)
- Minimalizátory skalárních jednorozměrných funkcí a vyhledávače kořenů (např. minimize_scalar a root_scalar)
- Řešiče soustav vícerozměrných rovnic pomocí algoritmů, jako je hybridní Powell, Levenberg-Marquardt.
Rosenbrookova funkce:
Rosenbrookova funkce ( rosen) je testovací problém používaný pro optimalizační algoritmy založené na gradientu. Ve SciPy je definována takto:

PŘÍKLAD:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
Výstup: 7371.0399999999945
Nelder-Mead:
Nelder-Meadova metoda je numerická metoda často používaná k nalezení minima/maxima funkce ve vícerozměrném prostoru. V následujícím příkladu je použita metoda minimalizace spolu s algoritmem Nelder-Mead.
PŘÍKLAD:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
Výstup: array()
Interpolační funkce:
V oblasti numerické analýzy se interpolací rozumí konstrukce nových datových bodů v rámci množiny známých datových bodů. Knihovna SciPy se skládá z podbalíčku s názvem scipy.interpolate, který se skládá ze spline funkcí a tříd, jednorozměrných a vícerozměrných (jednorozměrných a vícerozměrných) interpolačních tříd atd.
Jednorázová interpolace:
Jednorázová interpolace je v podstatě oblast fitování křivek, která nachází křivku, jež poskytuje přesné přizpůsobení řadě dvourozměrných datových bodů. SciPy poskytuje funkci interp1d, kterou lze využít k vytvoření univariační interpolace.
PŘÍKLAD:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
VÝSLEDEK:
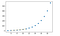
Multivariační interpolace:
Multivariační interpolace (prostorová interpolace ) je druh interpolace na funkce, které se skládají z více než jedné proměnné. Následující příklad demonstruje příklad
Interpolace přes 2-D síť pomocí funkce interp2d(x, y, z) v podstatě použije pole x, y, z k aproximaci nějaké funkce interp2d. f: „z = f(x, y)“ a vrátí funkci, jejíž metoda volání použije spline interpolaci k nalezení hodnoty nových bodů.
PŘÍKLAD:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
VÝSTUP:

Fourierova transformace funkcí:
Fourierova analýza je metoda, která se zabývá vyjádřením funkce jako součtu periodických složek a obnovením signálu z těchto složek. Pomocí funkcí fft lze vrátit diskrétní Fourierovu transformaci reálné nebo komplexní posloupnosti.
PŘÍKLAD:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
VÝSTUP:
Podobně lze zjistit inverzní hodnotu pomocí funkce ifft takto:
PŘÍKLAD:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
VÝSTUP:
Funkce zpracování signálů:
Zpracování signálů se zabývá analýzou, úpravou a syntézou signálů, jako je zvuk, obraz atd. SciPy poskytuje několik funkcí, pomocí kterých můžete navrhovat, filtrovat a interpolovat jednorozměrná a dvourozměrná data.
Filtrování:
Filtrováním signálu z něj v podstatě odstraňujete nežádoucí složky. Chcete-li provést uspořádané filtrování, můžete využít funkci order_filter. Tato funkce v podstatě provádí uspořádané filtrování na poli. Syntaxe této funkce je následující:
SYNTAX:
order_filter(a, domain, rank)
a = N-rozměrné vstupní pole
doména = maskovací pole, které má stejný počet rozměrů jako `a`
rank = nezáporné číslo, které vybírá prvky ze seznamu po jeho seřazení (0 je nejmenší, následuje 1…)
PŘÍKLAD:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
The scipy.Signal podbalíček se také skládá z různých funkcí, které lze použít ke generování průběhů. Jednou z takových funkcí je chirp. Tato funkce je generátorem kosinusových křivek s frekvenčním posunem a její syntaxe je následující:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear‘, phi=0, vertex_zero=True)
where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:

Lineární algebra:
Lineární algebra se zabývá lineárními rovnicemi a jejich reprezentací pomocí vektorových prostorů a matic. SciPy je postaven na knihovnách ATLAS LAPACK a BLAS a je extrémně rychlý při řešení problémů souvisejících s lineární algebrou. Kromě všech funkcí z numpy.linalg poskytuje scipy.linalg také řadu dalších pokročilých funkcí. Také pokud se nepoužívá numpy.linalg spolu s podporou ATLAS LAPACK a BLAS, je scipy.linalg rychlejší než numpy.linalg.
Nalezení inverzní matice:
Matematicky je inverzní matice A taková matice, kde je matice identity složená z jedniček po hlavní diagonále označená jako B=A-1. Scipy.linalg je také rychlejší než numpy.linalg. V programu SciPy lze tuto inverzi získat pomocí metody linalg.inv.
PŘÍKLAD:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
VÝSLEDEK:
]
Zjištění determinantů:
Hodnota odvozená aritmeticky z koeficientů matice se nazývá determinant čtvercové matice. Ve SciPy to lze provést pomocí funkce det, která má následující syntaxi:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
kde,
a : (M, M) Je čtvercová matice
overwrite_a( bool, nepovinné) : Umožňuje přepsání dat v a
check_finite ( bool, nepovinné): Kontrola, zda se vstupní matice skládá pouze z konečných čísel
PŘÍKLAD:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
VÝSTUP: -5.0
Sparse Eigenvalues:
Vlastní čísla jsou specifickou množinou skalárů spojených s lineárními rovnicemi. ARPACK poskytuje, že umožňuje najít vlastní hodnoty ( vlastní vektory ) poměrně rychle. Kompletní funkčnost ARPACKu je zabalena do dvou vysokoúrovňových rozhraní, kterými jsou scipy.sparse.linalg.eigs a scipy.sparse.linalg.eigsh. eigs. Rozhraní eigs umožňuje najít vlastní čísla reálných nebo komplexních nesymetrických čtvercových matic, zatímco rozhraní eigsh obsahuje rozhraní pro reálné symetrické nebo komplexně hermitovské matice.
Funkce eigh řeší zobecněný problém vlastních čísel pro komplexně hermitovskou nebo reálnou symetrickou matici.
PŘÍKLAD:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
VÝSTUP:
Vybraná vlastní čísla :
Komplexní ndarray :
]
Prostorové datové struktury a algoritmy:
Prostorová data se v podstatě skládají z objektů, které se skládají z linií, bodů, ploch atd. Balíček scipy.spatial programu SciPy dokáže pomocí knihovny Qhull vypočítat Voronoiovy diagramy, triangulaci atd. Obsahuje také implementaci KDTree pro dotazy na nejbližší sousední body.
Delaunayovy triangulace:
Matematicky je Delaunayova triangulace pro množinu diskrétních bodů v rovině taková triangulace, že žádný bod v dané množině bodů není uvnitř obvodu žádného trojúhelníku.
PŘÍKLAD:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
VÝSTUP:

Funkce zpracování vícerozměrného obrazu:
Zpracování obrazu se v podstatě zabývá prováděním operací s obrazem za účelem získání informací nebo získání vylepšeného obrazu z původního. Balík scipy.ndimage obsahuje řadu funkcí pro zpracování a analýzu obrazu, které jsou určeny pro práci s poli libovolné dimenzionality.
Konvoluce a korelace:
SciPy poskytuje řadu funkcí, které umožňují korelaci a konvoluci obrázků.
- Funkci correlate1d lze použít k výpočtu jednorozměrné korelace podél dané osy
- Funkce correlate umožňuje vícerozměrnou korelaci libovolného pole se zadaným jádrem
- Funkci convolve1d lze použít k výpočtu jedno-rozměrnou konvoluci podél dané osy
- Funkce convolve umožňuje vícerozměrnou konvoluci libovolného daného pole se zadaným jádrem
PŘÍKLAD:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
Výstup: array()
Soubor IO:
Scipy.io poskytuje řadu funkcí, které vám pomohou spravovat soubory různých formátů, jako jsou soubory MATLABu, soubory IDL, soubory Matrix Marketu atd.
Chcete-li tento balíček využít, musíte jej importovat následujícím způsobem:
import scipy.io as sio
Kompletní informace o podbalíčku najdete v oficiálním dokumentu o File IO.
Tímto se dostáváme na konec tohoto SciPy Tutoriálu. Doufám, že jste vše jasně pochopili. Ujistěte se, že si co nejvíce procvičujete.
Pokud se chcete podívat na další články o nejtrendovějších technologiích na trhu, jako je umělá inteligence, DevOps, etický hacking, pak se můžete podívat na oficiální stránky Edureka.
Věnujte pozornost dalším článkům z této série, které budou vysvětlovat různé další aspekty Pythonu a datové vědy.
1. Učebnice Pythonu. Klasifikátor strojového učení v Pythonu
2. Tahák pro Python Scikit-Learn
3. Nástroje pro strojové učení
4. Knihovny Pythonu pro datovou vědu a strojové učení
5. Strojové učení v Pythonu. Chatbot v Pythonu
6. Kolekce v Pythonu
7. Moduly Pythonu
8. Dovednosti vývojáře v Pythonu
9. Python. Otázky a odpovědi na pohovory týkající se OOP
10. Životopis vývojáře v jazyce Python
11. Průzkumná analýza dat v jazyce Python
12. Hadí hra s modulem Turtle v jazyce Python
13. Plat vývojáře v jazyce Python
14. Analýza hlavních komponent
15. Python versus C++
16. Výukový program Scrapy
17. Škrabání webu pomocí Pythonu
18. Regresní metoda nejmenších čtverců
19. Zápisník Jupyter Cheat Sheet
20. Základy Pythonu
21. Vzorce programů v jazyce Python
22. Generátory v jazyce Python
23. Dekorátor v jazyce Python
24. IDE Python Spyder
25. Mobilní aplikace pomocí Kivy v Pythonu
26. Deset nejlepších knih pro výuku &praktického Pythonu
27. Robotický framework v Pythonu
28. Hadí hra v Pythonu pomocí PyGame
29. Otázky a odpovědi k pohovoru o Django
30. Deset nejlepších aplikací v jazyce Python
31. Hašovací tabulky a hašmapy v jazyce Python
32. Python 3.8
33. Stroj s podpůrnými vektory
34. Výukový kurz jazyka Python