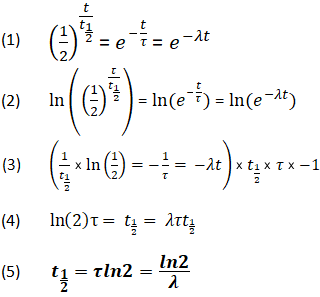Následující nástroje dokáží vygenerovat libovolnou z dalších tří hodnot ve vzorci pro poločas rozpadu látky, který se sníží na polovinu.

Kalkulačka poločasu rozpadu
Pro výpočet čtvrté hodnoty uveďte libovolné tři z následujících údajů.
Převod poločasu života, střední doby života a rozpadové konstanty
Prosím, uveďte některou z následujících možností, jak získat další dvě.
Definice a vzorec
Poločas života je definován jako doba, za kterou se daná veličina sníží na polovinu své původní hodnoty. Termín se nejčastěji používá v souvislosti s atomy procházejícími radioaktivním rozpadem, ale lze jej použít i k popisu jiných typů rozpadu, ať už exponenciálního, nebo ne. Jednou z nejznámějších aplikací poločasu rozpadu je datování pomocí uhlíku 14. Poločas rozpadu uhlíku-14 je přibližně 5 730 let a lze jej spolehlivě použít k měření dat až do doby před přibližně 50 000 lety. Postup datování pomocí uhlíku-14 vyvinul William Libby a je založen na skutečnosti, že uhlík-14 se v atmosféře neustále tvoří. Při fotosyntéze se dostává do rostlin a při konzumaci rostlin do živočichů. Uhlík-14 podléhá radioaktivnímu rozpadu, jakmile rostlina nebo živočich zemře, a měření množství uhlíku-14 ve vzorku poskytuje informaci o tom, kdy rostlina nebo živočich zemřeli.
Níže jsou uvedeny tři ekvivalentní vzorce popisující exponenciální rozpad:
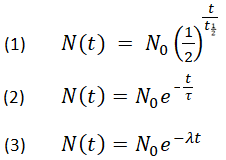
- kde
N0 je počáteční množství
Nt je zbývající množství po čase, t
t1/2 je poločas rozpadu
τ je střední doba života
λ je rozpadová konstanta
Pokud by archeolog našel fosilní vzorek, který by obsahoval 25 % uhlíku-14 ve srovnání s živým vzorkem, čas smrti fosilního vzorku by mohl být určen přeskládáním rovnice 1, protože jsou známy hodnoty Nt, N0 a t1/2. Na základě této rovnice by bylo možné určit, kdy fosilní vzorek zemřel.
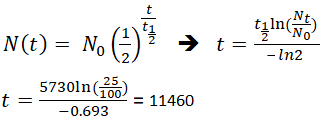
To znamená, že fosilie je stará 11 460 let.
Derivace vztahu mezi konstantami poločasu života
Pomocí výše uvedených rovnic je také možné odvodit vztah mezi t1/2, τ a λ. Tento vztah umožňuje určit všechny hodnoty, pokud je známa alespoň jedna.