Proporcionální řízení je jen jedním ze způsobů, jak reagovat na chybu v systému. Problémem proporcionálního řízení je, že nedokáže rozpoznat trendy a přizpůsobit se jim. To je úkolem integrálního řízení.
Vlevo na obrázku 6 je další příklad grafu chyby v systému v čase. Opět se může jednat o vzdálenost robota od objektu, nebo o hladinu kapaliny v nádrži či teplotu v tovární peci. Možná se cíl, který robot sleduje, od robota stále vzdaluje rychlostí, kterou robot nestíhá. Možná je opotřebované těsnění dvířek trouby; možná je odběr kapaliny z nádrže neobvykle velký. Bez ohledu na příčinu, protože proporcionální systém není navržen tak, aby reagoval na trendy, nemůže problém odhalit a opravit. Proto přichází na řadu integrální regulace.
Integrální měří oblast mezi hodnotami chyby a časovou osou. Pokud se chyba nevrací k nule, plocha chyby se stále zvětšuje. Pravá strana obrázku 6 ukazuje, jak může integrální výstup reagovat na tento druh trendu. Jak se zvětšuje plocha mezi křivkou chyby a časovou osou, výstup se zvětšuje úměrně této ploše. Výsledkem je, že výstup pohání pohon stále silněji, aby chybu opravil.
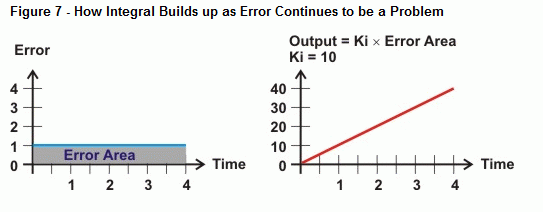
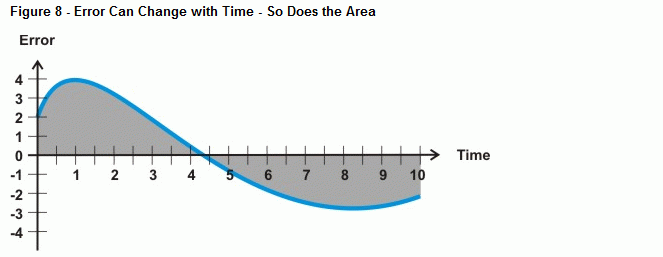
Co se tedy stane, když chyba není přímka, jako křivka na obrázku 8? To určuje početní operace integrace, plocha mezi křivkou a osou. V případě integrálního řízení platí, že čím více času uplyne s chybou, tím více roste plocha pod křivkou a tím i hodnota, kterou integrální výpočet použije k řízení proti chybě systému. Pokud křivka chyby klesne pod časovou osu, odečte se nárůst záporné plochy od nárůstu kladné plochy. Při správném nastavení může integrální řízení pomoci systému zdokonalit se na nulovou chybu.
Znak BASIC může aproximovat chybu pod křivkou pomocí numerické integrace. Obrázek 9 ukazuje, jak lze aproximovat chybu pod křivkou sečtením plochy svazku malých obdélníků mezi křivkou chyby a časovou osou. Plocha každého políčka je chyba vynásobená časem mezi měřeními. Sečtením ploch všech políček získáte aproximaci plochy pod křivkou.
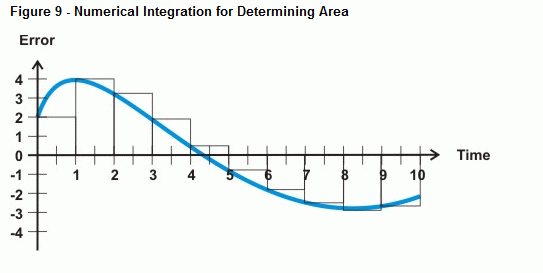
Pokud jsou vaše měření rovnoměrně rozložena, můžete šířku každého políčka nazvat hodnotou 1. Díky tomu je matematika mnohem jednodušší, než když se snažíte zohlednit 20 ms mezi vzorky, 5 minut mezi vzorky nebo jakoukoli vzorkovací frekvenci. Namísto násobení chyby časovým přírůstkem mezi vzorky a následného přičítání k další chybě vynásobené časem můžete prostě vynásobit každý vzorek chyby časem 1. Výsledkem je, že pro výpočet integrálu můžete prostě vést průběžný součet chybových měření. Zde je příklad, jak to provést pomocí PBASIC:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
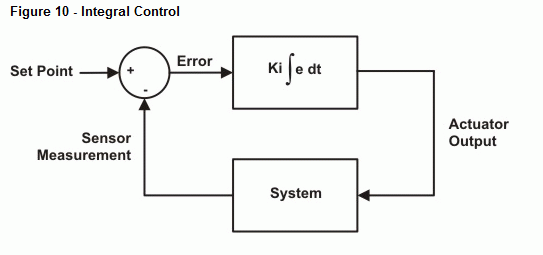
Další ukázkový program provede numerickou integraci na chybovém signálu a podle toho upraví výstup. Stejně jako u proporcionálního řízení existuje konstanta, která škáluje integrační výstup na požadovanou hodnotu. Pro zjednodušení použijeme pro Ki opět hodnotu 10. Na obrázku 10 je znázorněno blokové schéma regulační smyčky. Výraz Kp ∫ edt označuje Kp vynásobený integrálem chyby v čase. Jinými slovy, Kp vynásobené kumulovanou plochou mezi křivkou chyby a časovou osou.
Ukázkový program – IntegralAlgorithm.bs2
- Zadejte, uložte a spusťte IntegralAlgorithm.bs2.
- Zadejte tuto posloupnost hodnot do okénka vysílání Debug Terminal: 3 3 3 3 3 3 3 3 3. Všimněte si, jak se integrální výstup zvětšuje při každém opakování 3. To je práce integrálu, zjišťovat trendy a podle potřeby zvětšovat jednotku pro korekci.
- Nyní zkuste tuto sekvenci: 1 2 3 4 5 4 3 2 1 0 -1 -2 -3 -4 -3 -2 -1 0. Plocha pod touto křivkou je 0, protože záporná plocha je stejná jako kladná plocha. K tomu také dospěje integrální výpočet, když dokončíte zadávání posloupnosti.
' IntegralAlgorithm.bs2' Demonstrates how integral control influences error correction' in a feedback loop. ' {$STAMP BS2}' {$PBASIC 2.5} SetPoint CON 0 ' Set pointKi CON 10 ' Integral constant Current CON 0 ' Array index for current errorAccumulator CON 1 ' Array index for accumulated error sensorInput VAR Word ' Inputerror VAR Word(2) ' Two element error arrayi VAR Word ' Integral termdrive VAR Word ' Output DO DEBUG "Enter sensor input value: " DEBUGIN SDEC sensorInput ' Calculate error. error(Current) = SetPoint - sensorInput ' Calculate integral term. error(Accumulator) = error(Accumulator) + error(Current) i = Ki * error(Accumulator) ' Calculate output. drive = i ' Display values. DEBUG CR, CR, "ERROR", CR, SDEC ? SetPoint, SDEC ? sensorInput, SDEC ? error(Current), CR, "INTEGRAL", CR, SDEC ? Ki, SDEC ? error(accumulator), SDEC ? i, CR, "OUTPUT", CR, SDEC ? i, SDEC ? drive, CR, CR LOOP
Jak funguje IntegralAlgorithm.bs2
Tento program je ProportionalAlgorithm.bs2 upravený tak, aby místo toho prováděl integrální výpočet. Nyní je třeba sledovat dva různé typy chyb, takže tam bylo pole proměnných chyb rozšířeno na dva prvky. Proměnná error(0) sleduje aktuální chybu a error(1) sleduje kumulovanou chybu. Díky konstantám Current CON 0 a Accumulator CON 1 je účtování pomocí error(current) a error(accumulator) o něco rozumnější.
Další změna, která byla provedena, spočívá v tom, že chyba se kumuluje a integrální výstup se počítá pomocí těchto dvou příkazů:
' Calculate integral term.error(Accumulator) = error(Accumulator) + error(Current)i = Ki * error(Accumulator)
Váš tah – upínání integrálního výstupu
Jak jste možná pochopili z opakovaného zadávání 3 do ladicího terminálu, integrální výstup pohonu může opravdu začít utíkat. Pomocí operátorů MIN a MAX můžete integrálnímu řízení zabránit, aby to s výstupem přehnalo. Zopakujme činnost se servopohonem a omezme výstup od 650 do 850.
- Změňte příkaz drive = i na drive = i + Offset MIN 650 MAX 850.
- Spustíme program a ověříme, že integrální výstup je omezen na hodnoty mezi 650 a 850. Zkuste opakovaně zadat 2 a pak opakovaně -2.
.