Rotační kinematika - Fyzika 298

„Lidé mluví o zabíjení času, zatímco čas tiše zabíjí je“
Dion Boucicault – London Assurance (1841)

Dosud jsme se zabývali kinematikou a dynamikou částic, včetně translačního a kruhového pohybu a translačního pohybu soustav částic (zejména tuhých těles) z hlediska pohybu středu hmotnosti soustavy (tělesa). V posledním případě si můžeme představit, že veškerá hmotnost objektu se nachází v jeho středu, pokud jde o vnější translační síly.

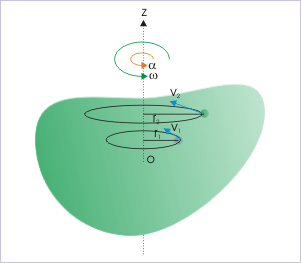Dalším krokem je úvaha o rotaci tuhého tělesa kolem pevné osy otáčení. Všimněte si, že protože uvažujeme tuhé těleso, každá částice v tělese zůstává vůči ostatním pevná. To znamená, že při takovém rotačním pohybu se každá částice pohybuje po kružnici, jejíž střed leží na ose otáčení. Na obrázku vpravo se objekt otáčí kolem osy z; dvě částice vzorku se pohybují po kružnicích o poloměrech r1 a r2. Pokud můžeme popsat kruhový pohyb částice bez přímého odkazu na její poloměr, pak budou všechny částice v systému popsány stejnou soustavou rovnic. Přestože poloměry částic jsou různé, jejich úhlové natočení je totožné. Protoje nutné zavést úhlové proměnné.

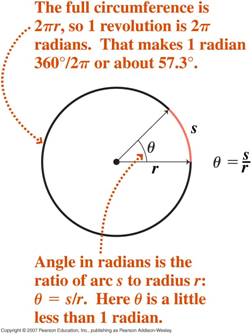
Radiánová míra úhlů

Úhlová rychlost (rychlost) a úhlové zrychlení

Úhlová rychlost a úhlové zrychlení jsou definovány podobně jako rychlost a zrychlení. U každého z nich existují průměrné a okamžité hodnoty.

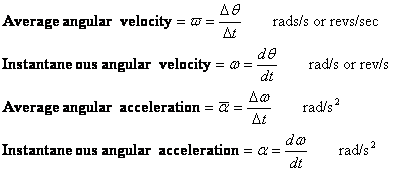
Úhlové zrychlení není totéž co dostředivé zrychlení. Dostředivé zrychlení je způsobeno změnou směru rychlosti, úhlové zrychlení je způsobeno změnou velikosti rychlosti (prostřednictvím úhlu natočení).

Přesně jako v případě translace je rozdíl mezi úhlovou rychlostí a úhlovou rychlostí ve směru. Úhlová rychlost musí obsahovat směr otáčení kolem dané osy. Například 10 rad/s ve směru hodinových ručiček kolem osy x je úhlová rychlost, 10 rad/s kolem osy x je úhlová rychlost.

Rotační kinematické rovnice

Přímou analogií s translačními kinematickými rovnicemi lze kruhový pohyb kolem jedné osy při konstantním úhlovém zrychlení popsat pomocí následujících čtyř rovnic,

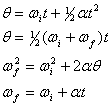
kde jsme provedli substituce,

Všimněte si, že stejně jako +x je definováno libovolně doprava, kladná hodnota theta může být definována jako pravotočivá nebo levotočivá.

Vztah mezi úhlovou a translační veličinou

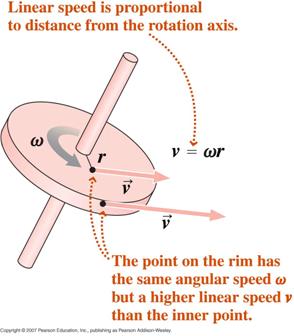Vycházejíce z definice radiánové míry, diferencováním vzhledem k času můžeme ukázat, že,

kde v je tečná rychlost a a je tečné zrychlení.

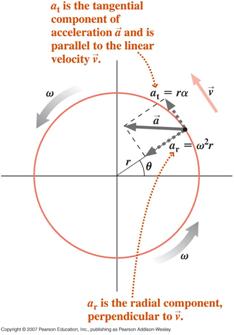
Částice vykonávající kruhový pohyb s měnící se úhlovou rychlostí (nerovnoměrný kruhový pohyb) bude mít dvě složky zrychlení, tangenciální složku v důsledku měnící se velikosti její rychlosti a radiální (dostředivou) složku v důsledku měnícího se směru její rychlosti

Čisté zrychlení částice je vektorový součet těchto dvou složek, jak je uvedeno níže.

Pro informaci…

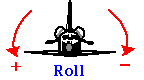
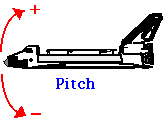
Současnou rotaci kolem více než jedné osy lze uvažovat podobně jako pohyb projektilu, kdy jsme naši 1D translační diskusi rozšířili na 2D pohyb. V leteckých aplikacích se rotace kolem tří os popisují jako Roll, Pitch a Yaw.