
Neuronové sítě a matematika jsou neoddělitelné a to asi většinu lidí děsí. Slyšel jsem o Deep Learningu až příliš mnoho pochybovačných poznámek: „Ach, to je příliš mnoho matematiky na to, abych to pochopil“, „Kolik firem opravdu používá Deep Learning? Raději si ušetřím mozkové závity a budu se od těchto náročných konceptů držet dál.“
Ale když se nad tím zamyslíte, tak to zase tak složité není. Věřte mi! Abychom pochopili, proč se algoritmus chová určitým způsobem, je nezbytné pochopit, co se děje v zákulisí. Složité algoritmy strojového učení jsou dnes pro nás pohodlně zabaleny a stačí je zavolat funkcí. Derivace aktivačních funkcí jsou poněkud méně zřejmé pojmy, které máme často tendenci ignorovat. Tvoří však základ výkonných algoritmů a vynaložit trochu úsilí navíc na jejich pochopení se rozhodně vyplatí. Po přečtení tohoto článku budete o krok blíže k odhalení toho, co se skrývá pod fasádou „černé skříňky“.
Základní informace
Neuronové sítě používají ke katalyzování procesu učení různé aktivační funkce ve skryté a výstupní vrstvě. Mezi několik běžně používaných aktivačních funkcí patří sigmoidní funkce a funkce tanH. Nejoblíbenější aktivační funkcí je ReLU ( Rectified Linear Unit), protože dokáže účinně překonat problém mizejícího gradientu. Hlubší vhled do aktivačních funkcí je na jindy. Dnes se zaměříme na matematiku, která se skrývá za derivací Sigmoidovy funkce.
Proč je důležitá derivace aktivační funkce?
Jak asi víte, neuronové sítě se řídí dvěma kroky:
- Propagace směrem dopředu – vstupní data procházejí sítí a my získáváme předpovězený výstup. Porovnáme jej se skutečným výstupem a vypočítáme chybu.
- Zpětné šíření – Vypočtená chyba se použije k aktualizaci parametrů neuronové sítě pomocí derivace aktivační funkce.
Sigmoidní funkce
Sigmoidní funkce, charakterizovaná křivkou ve tvaru písmene S, se často označuje jako zvláštní případ logistické funkce. Je nejužitečnější v případech, kdy máme jako výstup předpovědět pravděpodobnost.
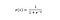
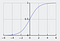
Sigmoidní funkce vynáší hodnoty, které leží mezi 0 a 1 (oprávněně vzhledem k tomu, že předpovídá pravděpodobnosti).
Sigmoidní derivace
Tento základní stavební prvek, který pomáhá trénovat neuronové sítě, má tvar:


Bez dalších podrobností, pojďme se pustit do derivace!
Přístup 1

Přístup 2:
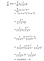
Proč používáme tuto verzi derivátu?
V kroku dopředného šíření vypočítáme sigmoidní funkci (σ(x)) a máme po ruce její hodnotu. Při výpočtu derivace v kroku zpětného šíření stačí do výše odvozeného vzorce dosadit hodnotu σ(x) a voilá, můžete začít!“
To je vše, pánové! Díky za přečtení!