Úvod
Souřadnicové transformace jsou ve 2D dost neintuitivní a ve 3D dost bolestivé. Tato stránka se jimi zabývá v následujícím pořadí: (i) vektory ve 2-D, (ii) tenzory ve 2-D, (iii) vektory ve 3-D, (iv) tenzory ve 3-D a konečně(v) tenzorové transformace 4. řádu.
Důležitým aspektem souřadnicových transformací je vyhodnocení transformační matice,zejména ve 3-D. Toho se zde dotkneme a podrobně o tom pojednáme na další stránce.
Je velmi důležité si uvědomit, že všechny souřadnicové transformace na této stránce jsou rotacemi souřadnicového systému, zatímco samotný objekt zůstává pevný. „Objektem“ může být vektor, například síla nebo rychlost, nebo tenzor, například napětí nebo deformace v součásti. Rotaci objektů se budeme věnovat v dalších částech.
2-D Transformace souřadnic vektorů
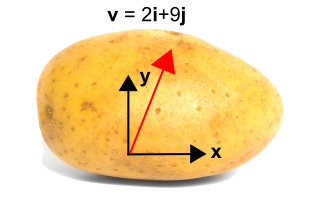
Akademická brambora poskytuje vynikající příklad toho, jak se transformace souřadnicaplikují na vektory, a zároveň zdůrazňuje, že se otáčí souřadnicový systém, a ne vektor… nebo brambora.
Brambora vlevo má na sobě vektor. Bez souřadnicového systému však není možné tento vektor popsat.Proto byl k bramboře přidán souřadnicový systém, jak je znázorněno vpravo, což nyní umožňuje popsat vektor jako \({\bf v} = 2{\bf i} + 9{\bf j}\).

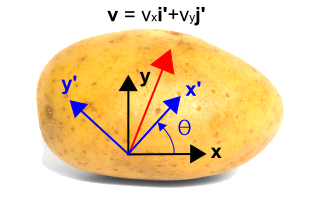
Nyní tedy zavedeme otočený souřadnicový systém znázorněný modře níže, pomocí\(x’\) a \(y’\). Nový systém je otočen proti směru hodinových ručiček o úhel \(\theta\) oproti původnímu souřadnicovému systému. Všimněte si, že samotný vektor se vůbec nemění. Je to stále stejný vektor jako předtím. V novém souřadném systému je však popsán jinými číselnými hodnotami. V tomto případě je vektor rovnoběžnější s novou osou \(x’\) než s osou \(y’\), takže složka \({\bf i‘}\) bude větší než složka \({\bf j‘}\). Transformace je uvedena pod obrázkem.
\\\
To lze vidět tak, že si všimneme, žeTyto čtyři činitele tvoří čtyři členy v rovnicích transformace. Lze je snadno ověřit nastavením \(\theta = 0^\circ \) a \(\theta = 90^\circ \). Když \(\theta = 0^\circ\), pak \(v’_x = v_x\) a \(v’_y = v_y\). Když \(\theta = 90^\circ\), pak \(v’_x = v_y\) a \(v’_y = -v_x\).
Transformační matice
Pohodlnější je zapisovat transformační rovnice (a pracovat s nimi) pomocí matic.
\\\levice\{ \matice {v_x \\ v_y} \pravá\}\]
Členy \(\cos \theta\) jsou na diagonále matice, zatímco členy \(\sin \theta\) jsou mimo diagonálu. Jediným potenciálním problémem je zapamatovat si, který člen \(\sin \theta\) má znaménko minus. Je to vždy levý dolní člen.
Výše uvedená rovnice se zapisuje v maticovém zápisu jako
\
kde \({\bf Q}\) je obvyklé písmeno zvolené pro transformační matici.

Transformační vs. rotační matice
Pokud by toto téma nebylo již tak dost složité, mnoho knih a webových stránek přispívá ke zmatku tím, že neobjasňuje, co je pevné a co je rotační. Na této a následující stránce je to souřadnicový systém, který se otáčí, zatímco objekt zůstává pevný.
Pro zdůraznění této skutečnosti je zde tedy použit termín transformační matice.
Později se však budeme zabývat situacemi, kdy se objekt otáčí, zatímco souřadnicový systém zůstává pevný. V tomto případě bude použit termín rotační matice, abychom zdůraznili, že objekt rotuje.
Mnoho nejasností vyplývá z úžasné skutečnosti, že každá matice (transformační a rotační) je pouze transpozicí té druhé! Vypadají tedy nesmírně podobně. Ve dvourozměrných problémech je jediný praktický rozdíl v tom, zda je znaménko minus před \(\sin \theta\) na členu \(q_{12}\), nebo na členu \(q_{21}\).
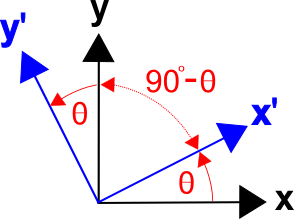
Existuje obecná metoda pro formulaci transformačních matic založená na kosinech úhlů mezi osami obou souřadnicových systémů, tj. na směrových kosinech. (To platí i pro trojrozměrné transformace.)Transformační matici lze zapsat jako
\\]
kde \((x‘,x)\) představuje úhel mezi osami \(x’\) a \(x\),\((x‘,y)\) je úhel mezi osami \(x’\) a \(y\) atd.
Úhel mezi \(x’\) a \(y\) je \((90^\circ – \theta)\) a \(\cos(x‘,y) = \cos(90^\circ – \theta) = \sin \theta\).
Také úhel mezi \(y’\) a \(x\) je \((90^\circ + \theta)\) a \(\cos(y‘,x) = \cos(90^\circ + \theta) = -\sin \theta\).
Tenzorový zápis
Transformace souřadnic se zapisuje v tenzorové notaci jako
\\
kde \(\lambda_{ij}\) je transformační matice \({\bf Q}\). (Nevím, proč se v maticovém zápisu používá \({\bf Q}\), ale v tenzorovém zápisu se používá \(\lambda_{ij}\), nikoli \(q_{ij}\).) \(\lambda_{ij}\) je definováno jako
\\
Příklad pokud \(i = 1\) a \(j = 2\), pak
\
\(\lambda_{ij}\) je směrový kosinus úhlu mezi osou \(x’_i\) a osou \(x_j\). Opět to platí i pro 3-D transformace.
2-D souřadnicové transformace tenzorů
V této části si představíme co a jak u tenzorových transformací, proč si budeme muset počkat na později.
Souřadnicové transformace tenzorů 2. řádu zahrnují stejnou matici \({\bf Q}\)jako vektorové transformace. Transformace tenzoru napětí, \(\boldsymbol{\sigma}\), z referenčního souřadnicového systému \(x-y\) na \(\boldsymbol{\sigma‘}\) v novém systému \(x‘-y’\) se provádí takto.
\
Při explicitním zápisu matic dostaneme
\ = \levá \levá \levá \]
(Všimněte si, že tenzor napětí je vždy symetrický, a to i po transformacích.)
Vynásobením matic získáme
\\
Tyto tři rovnice jsou přesně 2-D transformací tenzoru napětí vyplývajícího ze součtu sil na diferenciálním prvku a nastolení rovnováhy. To je také znázorněno Mohrovou kružnicí.
Tenzorový zápis
Transformace souřadnic se zapisuje v tenzorové notaci jako
\
Jak je obvyklé, tenzorový zápis poskytuje další vhled do procesu. Tentokrát tento vhled vyplývá z indexů na lambdách. Každá lambda ve skutečnosti páruje index na \(\tučný symbol{\sigma‘}\) s indexem na \(\tučný symbol{\sigma}\).To platí bez ohledu na hodnost tenzoru.
3-D transformace souřadnic vektorů
Mnoho obecných rovnic používaných při 2-D transformacích je použitelných i ve 3-D. Příklady zahrnují
\
Jen nyní se liší detaily. Vektory mají z-komponenty a transformační matice jsou 3×3 místo 2×2.
\\]
\\]
\\\{ \matrix { v_x \\ v_y \\ v_z } \right\}\]
3-D souřadnicové transformace tenzorů
Znovu opakuji, pravidla se nemění, mění se pouze podrobnosti.
\
Při explicitním zápisu matic dostaneme
\ = \left\left\left\]
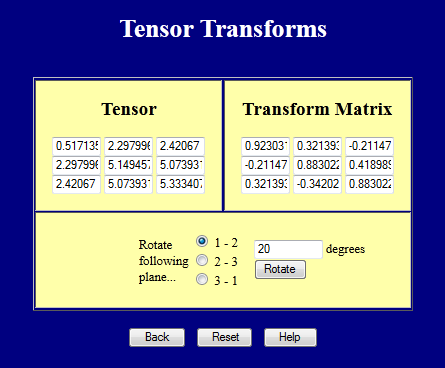
Tato webová stránka provádí souřadnicové transformace 3-D tenzorů. Vyzkoušejte si to.
Souřadnicové transformace tenzorů 4. řádu
V části o Hookově zákonu uvidíme, že tenzor tuhosti je4. řádu, tj. 3x3x3x3 (nikoliv 4×4). Zapisuje se jako \(C_{ijkl}\), protože se vztahuje k jakékoliv složce deformace, \(\epsilon_{kl}\), k jakékoliv složce napětí, \(\sigma_{ij}\), tj, \(\sigma_{ij} = C_{ijkl} \epsilon_{kl}\).Zákon transformace souřadnic pro tenzor tuhosti 4. řádu se snadno zapíše v tenzorové notaci jako
\
Tenzorová rovnice říká, jak zapsat transformaci v maticové notaci.
\
Souhrn
Souřadnicová transformace vektoru v maticovém a tenzorovém zápisu je
\
Souřadnicová transformace tenzoru v maticovém a tenzorovém zápisu je
\
Všimněte si, že \({\bf Q}\) a \(\lambda_{ij}\) jsou stejné transformační matice.
V 2-D jsou \({\bf Q}\) a \(\lambda_{ij}\) definovány jako
\\]
což je speciální případ obecnějšího 3-D tvaru
\\]
.