Jak se připravit na otázky z geometrie v testu z matematiky
Všeobecné informace
Geometrie je jen módní název pro studium přímek a tvarů. Určitě existují další složité principy a témata, ale my zde máme základy. Než se pustíte do pokročilejších konceptů, budete je muset zvládnout.
(Vezměte prosím na vědomí, že pokud je obrázek v této příručce označen jako „příklad“, nemusí to být jediné znázornění daného obrázku, ale je jedním z nich)
Body a čáry
Bod v geometrii je místo. Nemá délku, šířku ani hloubku. K označení bodu používáme tečku a velké písmeno.
Úsečka je určena dvěma body a všemi body mezi nimi. Tyto dva body se nazývají koncové body úsečky. Úsečka má jeden rozměr: délku. Chcete-li úsečku zapsat, umístěte nad oba koncové body čárku. \(\overline{AB}\) nebo \(\overline{BA}\) je tato úsečka:

Úsečka se táhne oběma směry bez konce. Úsečku zapíšete tak, že nad libovolné dva body úsečky umístíte sloupec se dvěma šipkami. \(\overleftrightarrow{AB}\) nebo \(\overleftrightarrow{BA}\) je přímka:

Prvek začíná v jednom koncovém bodě a táhne se bez konce pouze jedním směrem. Chcete-li paprsek zapsat, umístěte čáru se šipkou směřující doprava nad dva body: koncový bod a libovolný další bod (v daném směru). \(\overrightarrow{AB}\) je paprsek:

Poznámka: nelze zapsat paprsek se šipkou směřující doleva jako \(\overleftarrow{BA}\). Důležité je také pořadí. \(\overrightarrow{BA}\) není stejné jako \(\overrightarrow{AB}\). První písmeno je vždy počátečním bodem paprsku.
Dvě přímky, úsečky nebo paprsky jsou kolmé, pokud svírají pravý úhel (viz níže). Pro označení kolmosti používejte symbol \(\perp\). Například pokud je \(\overline{AB}\) kolmá na \(\overline{CD}\), můžete napsat \(\overline{AB} \perp \overline{CD}\).
Příklad: 
Dvě přímky jsou rovnoběžné, pokud se nikdy neprotínají. Je-li \(\overleftrightarrow{AB}\) rovnoběžná s \(\overleftrightarrow{CD}\), můžeme napsat \(\overleftrightarrow{AB} \paralelní \overleftrightarrow{CD}\).
Příklad: 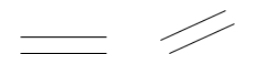
Rovinné útvary
V geometrii je rovina rovná dvourozměrná plocha, která se táhne nekonečně daleko. Tyto dva rozměry jsou délka a šířka. Rovinné útvary jsou tedy „ploché“ útvary, jako jsou čtverce, kružnice a trojúhelníky.
Obvyklé útvary
Polygon je uzavřená plocha v rovině ohraničená úsečkami zvanými strany.
Příklad: 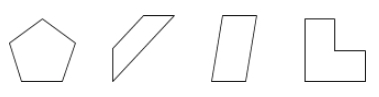
Pravidelný mnohoúhelník je mnohoúhelník, v němž jsou všechny úsečky a vnitřní úhly shodné.
Příklady:
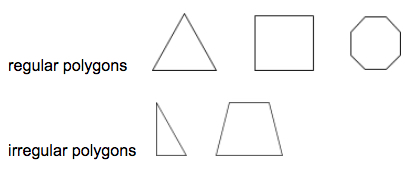
Trojúhelník je trojúhelník.
Příklady:
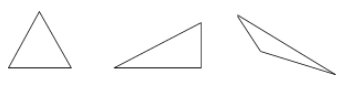
Čtyřúhelníky – čtyřstranné mnohoúhelníky
Rovnoběžník je typ čtyřúhelníku, jehož protilehlé strany jsou rovnoběžné a shodné. Protilehlé úhly rovnoběžnostěnu jsou také shodné.
Příklad: 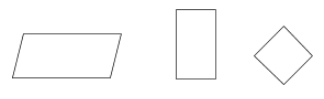
Obdélník je rovnoběžník se čtyřmi pravými úhly.
Příklady: 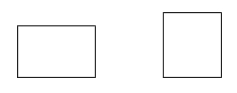
Rombus je rovnoběžník, jehož všechny čtyři strany jsou shodné.
Příklady: 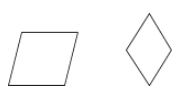
Čtverec je rovnoběžník, který je zároveň kosočtvercem i obdélníkem (všechny strany jsou shodné a všechny úhly jsou pravé).
Příklady: 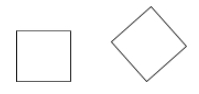
Lepid je čtyřúhelník, který má pouze jednu dvojici rovnoběžných stran.
Příklad: 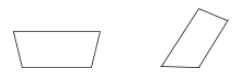
Polygony s více než čtyřmi stranami
\
\(^1\) Mnohoúhelník s 11 stranami můžeme také nazvat endekagon nebo undekagon.
Měření tvarů
Obvod je celková vzdálenost kolem mnohoúhelníku. Obvod zjistíte tak, že sečtete délky všech stran. Pokud je mnohoúhelník pravidelný (všechny strany jsou shodné) a délka jedné strany je \(s\), pak pro zjištění obvodu vynásobte počet stran \(s\). Například obvod pravidelného pětiúhelníku je \(P_\text{pravidelný pětiúhelník}=5s\)
.