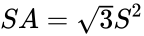Tetrahedron

Pravidelný tetraedr
(Pro rotační model klikněte zde)
Typ	Platonické těleso
Prvky	F = 4, E = 6 V = 4 (χ = 2)
Strany podle stran	4{3}
Schläfliho symbol	{3,3} a s{2,2}
Wythoffův symbol	3 | 2 3 | 2 2 2
Coxeter-Dynkinův
Symetrie	Td nebo (*332)
	U01, C15, W1
Vlastnosti	Pravidelný konvexní deltaedr
Dihedrální úhel	70.528779° = arccos(1/3)
3.3.3 (vrcholový útvar)	Samostatný duální (duální mnohostěn)
Síť

Tetraedr (množné číslo: tetraedr) je mnohostěn složený ze čtyř trojúhelníkových stěn, z nichž tři se setkávají v každém vrcholu. Pravidelný čtyřstěn je takový, v němž jsou čtyři trojúhelníky pravidelné neboli „rovnostranné“, a je jedním z platónských těles.

Čtyřstěn je jedním z druhů jehlanu, což je mnohostěn s plochou mnohoúhelníkovou podstavou a trojúhelníkovými stěnami spojujícími podstavu se společným bodem. V případě čtyřstěnu je základnou trojúhelník (za základnu lze považovat kteroukoli ze čtyř stěn), proto se čtyřstěn nazývá také trojboký jehlan nebo digonální deltaedr.

Vzorce pro pravidelný čtyřstěn

Objem je

Povrch je

Šablona:Commonscat

• F. M. Jackson a Weisstein, Eric W., „Tetrahedron“ z MathWorld.
• Weisstein, Eric W., „Tetrahedron“ z MathWorld.
• Weisstein, Eric W., „Tetrahedron“ z MathWorld.
• Jednotlivé mnohostěny
• Tetrahedron: Interaktivní model mnohostěnu
• K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra
• Vzorec Piera della Francesca pro objem čtyřstěnu na MathPages
• Volné papírové modely čtyřstěnu a mnoha dalších mnohostěnů
• Úžasný, vyplňující prostor, nepravidelný tetraedr, který obsahuje také popis „rotujícího prstence tetraedrů“, známého také jako kaleidocyklus.
• Jádrová síť tetraedru Aplikace tetraedrické struktury k vytvoření odolné datové sítě s částečnými sítěmi
• Explicitní přesné vzorce pro tenzor setrvačnosti libovolného tetraedru z hlediska jeho vrcholových souřadnic
• Tenzor setrvačnosti tetraedru

.