Vzorce pro Pí

Posted on by admin
Teorie čísel > Konstanty > Pí >
Výpočet a analýza > Řady > Vzorce pro BBP >
Výpočet a analýza > Výpočet >. Integrály > Určité integrály >
MathWorld Příspěvky > Cloitre >
MathWorld Příspěvky > Plouffe >
MathWorld Příspěvky > Sondow >

Less…

Zápisník Mathematica ke stažení

Existuje mnoho vzorců pi mnoha typů. Patří mezi ně mimo jiné řady, součin, geometrické konstrukce, limity, speciální hodnoty a iterace pí.

pi úzce souvisí s vlastnostmi kružnic a koulí. Pro kruh o poloměru r, jsou obvod a povrch dány vztahem

C = 2pir
(1)
A = pir^2.
(2)

Podobně pro kouli o poloměru r, plocha a uzavřený objem jsou

.

S = 4pir^2
(3)
V = 4/3pir^3.
(4)

Přesný vzorec pro pi ve smyslu inverzních tečen jednotkových zlomků je Machinův vzorec

1/4pi=4tan^(-1)(1/5)-tan^(-1)(1/(239)).
(5)

Existují tři další Machinovy vzorce,stejně jako tisíce dalších podobných vzorců, které mají více členů.

GregorySeries

Gregory a Leibniz zjistili

pi/4 = součet_(k=1)^(infty)((-.1)^(k+1))/(2k-1)
(6)
= 1-1/3+1/5-....
(7)

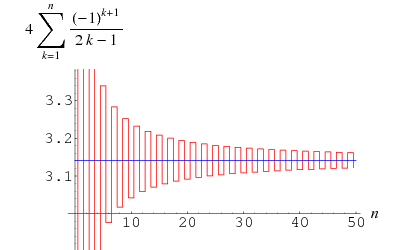
(Wells 1986, s. 50), která je známá jako Gregorova řada a lze ji získat dosazením x=1 do Leibnizovy řady pro tan^(-1)x. Chyba za ntým členem této řady v Gregoryho řadě je větší než (2n)^(-1), takže tento součet konverguje tak pomalu, že 300 členů nestačí ke správnému výpočtu pi na dvě desetinná místa! Lze jej však převést na

pi=součet_(k=1)^infty(3^k-1)/(4^k)zeta(k+1),
(8)

kde zeta(z) je Riemannova zeta funkce (Vardi 1991, str. 157-158; Flajolet a Vardi 1996), takže chyba po k členech je přibližně (3/4)^k.

Nekonečná součtová řada k Abrahamu Sharpovi (cca. 1,5 milionu let) je

. 1717) je dána vztahem

pi=sum_(k=0)^infty(2(-1)^k3^(1/2-k))/(2k+1)
(9)

(Smith 1953, s. 311). Další jednoduché řady, v nichž se objevuje pi, jsou

.

.

1/4pisqrt(2) = sum_(k=1)^(infty)
(10)
= 1+1/3-1/5-1/7+1/9+1/(11)-...
(11)
1/4(pi-3) = součet_(k=1)^(infty)((-.1)^(k+1))/(2k(2k+1)(2k+2))
(12)
= 1/(2-3-4)-1/(4-5-6)+1/(6-7-8)-...
(13)
1/6pi^2 = sum_(k=1)^(infty)1/(k^2)
(14)
= 1+1/4+1/9+1/(16)+1/(25)+...
(15)
1/8pi^2 = sum_(k=1)^(infty)1/((2k-.1)^2)
(16)
= 1+1/(3^2)+1/(5^2)+1/(7^2)+....
(17)

(Wells 1986, s. 53).

V roce 1666, Newton použil geometrickou konstrukci k odvození vzorce

pi = 3/4sqrt(3)+24int_0^(1/4)sqrt(x-x^2)dx
(18)
= (3sqrt(3))/4+24(1/(12)-1/(5-2^5)-1/(28-2^7)-1/(72-2^9)-....),
(19)

které použil k výpočtu pi (Wells 1986, s. 50; Borwein a kol. 1989; Borwein a Bailey 2003, s. 105-106). Koeficienty lze zjistit z integrálu

I(x) = intsqrt(x-x^2)dx
(20)
= 1/4(2x-1)sqrt(x-x^2)-1/8sin^(-1)(1-2x)
(21)

přirozeným rozkladem řady I(x)-I(0) kolem nuly, obtaining

I(x)=2/3x^(3/2)-1/5x^(5/2)-1/(28)x^(7/2)-1/(72)x^(9/2)-5/(704)x^(11/2)+...
(22)

(OEIS A054387 a A054388). Použitím Eulerovy transformace pro zlepšení konvergence dostaneme

pi/2 = 1/2sum_(n=0)^(infty)((n!)^22^(n+1))/((2n+1)!)=sum_(n=0)^(infty)(n!)/((2n+1)!!!)
(23)
= 1+1/3+(1-2)/(3-5)+(1-2-3)/(3-5-7)+...
(24)
= 1+1/3(1+2/5(1+3/7(1+4/9(1+.. ))))
(25)

(Beeler a kol. 1972, položka 120).

To odpovídá zapojení x=1/sqrt(2) do mocninné řady pro hypergeometrickou funkci _2F_1(a,b;c;x),

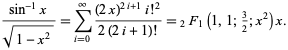(sin^(-1)x)/(sqrt(1-x^2))=sum_(i=0)^infty((2x)^(2i+1)i!^2)/(2(2i+1)!)=_2F_1(1,1;3/2;x^2)x.
(26)

Přes zlepšení konvergence řada (◇) konverguje pouze na jeden bit/termín. Za cenu odmocniny Gosper poznamenal, že x=1/2 dává 2 bity/termín,

1/9sqrt(3)pi=1/2sum_(i=0)^infty((i!)^2)/((2i+1)!),
(27)

a x=sin(pi/10) dává téměř 3.39 bitů/termín,

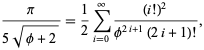pi/(5sqrt(phi+2))=1/2sum_(i=0)^infty((i!)^2)/(phi^(2i+1)(2i+1)!),
(28)

kde phi je zlatý řez. Gosper také získal

pi=3+1/(60)(8+(2-3)/(7-8-3)(13+(3-5)/(10-11-3)(18+(4-7)/(13-14-3)(23+...)))).
(29)

Agoritmus spigotu pro pi uvádějí Rabinowitz a Wagon (1995; Borwein a Bailey 2003, s. 141-142).

Ještě překvapivější je, že výraz v uzavřeném tvaru udávající algoritmus pro extrakci číslic, který dává číslice pi (nebo pi^2) v základu 16, objevili Bailey et al. (Bailey et al. 1997, Adamchik a Wagon 1997),

pi=sum_(n=0)^infty(4/(8n+1)-2/(8n+4)-1/(8n+5)-1/(8n+6))(1/(16))^n.
(30)

Tento vzorec, známý jako vzorec BBP, byl objeven pomocí algoritmu PSLQ (Ferguson et al. 1999) a je ekvivalentní vzorci

pi=int_0^1(16y-16)/(y^4-2y^3+4y-4)dy.
(31)

Pro pi v mocninách (-1)^k existuje řada vzorců typu BBP, z nichž prvních několik nezávislých vzorců je

pi = 4sum_(k=0)^(infty)((-1)^k)/(2k+1)
(32)
= 3sum_(k=0)^(infty)(-.1)^k
(33)
= 4sum_(k=0)^(infty)(-1)^k
(34)
= součet_(k=0)^(infty)(-1)^k
(35)
= sum_(k=0)^(infty)(-1)^k
(36)
= sum_(k=0)^(infty)(-1)^k.
(37)

Podobně existuje řada vzorců typu BBP pro pi v mocninách 2^k, z nichž prvních několik nezávislých vzorců je

.

.

.

pi = sum_(k=0)^(infty)1/(16^k)
(38)
= 1/2sum_(k=0)^(infty)1/(16^k)
(39)
= 1/(16)sum_(k=0)^(infty)1/(256^k)
(40)
= 1/(32)sum_(k=0)^(infty)1/(256^k)
(41)
= 1/(32)sum_(k=0)^(infty)1/(4096^k)
(42)
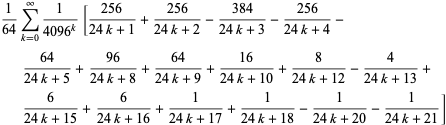= 1/(64)sum_(k=0)^(infty)1/(4096^k)
(43)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(44)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(45)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(46)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k)
(47)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k).
(48)

F. Bellard nalezl rychle konvergující BBP-vzorec

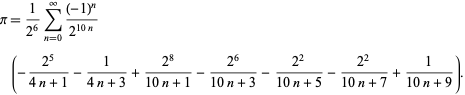pi=1/(2^6)sum_(n=0)^infty((-1)^n)/(2^(10n))(-(2^5)/(4n+1)-1/(4n+3)+(2^8)/(10n+1)-(2^6)/(10n+3)-(2^2)/(10n+5)-(2^2)/(10n+7)+1/(10n+9)).
(49)

Související integrál je

pi=(22)/7-int_0^1(x^4(1-x)^4)/(1+x^2)dx
(50)

(Dalzell 1944, 1971; Le Lionnais 1983, s. 22; Borwein, Bailey a Girgensohn 2004, s. 3; Boros a Moll 2004, s. 125; Lucas 2005; Borwein et al. 2007, s. 14). Tento integrál byl znám K. Mahlerovi v polovině 60. let a objevuje se ve zkoušce na univerzitě v Sydney v listopadu 1960 (Borwein, Bailey a Girgensohn, s. 3). Beukers (2000) a Boros a Moll (2004, s. 126) uvádějí, že není jasné, zda existuje přirozená volba racionálního polynomu, jehož integrál mezi 0 a 1 dává pi-333/106, kde 333/106 je další konvergentní. Pro čtvrtý konvergent však integrál existuje, a to

pi=(355)/(113)-1/(3164)int_0^1(x^8(1-x)^8(25+816x^2))/(1+x^2)dx.
(51)

(Lucas 2005; Bailey et al. 2007, s. 219). Ve skutečnosti Lucas (2005) uvádí několik dalších takových integrálů.

Backhouse (1995) použil identitu

I_(m,n) = int_0^1(x^m(1-x)^n)/(1+x^2)dx
(52)
= 2^(-(m+n+1))sqrt(pi)Gamma(m+1)Gamma(n+1)×_3F_2(1,(m+1)/2,(m+2)/2;(m+n+2)/2,(m+n+3)/2;-1)
(53)
= a+bpi+cln2
(54)

pro celé kladné číslo m a n a kde a, b a c jsou racionální konstanty pro vytvoření řady vzorců pro pi. Konkrétně, jestliže 2m-n=0 (mod 4), pak c=0 (Lucas 2005).

Podobný vzorec následně objevil Ferguson, což vede k dvourozměrné mřížce takových vzorců, kterou lze generovat pomocí těchto dvou vzorců daných vztahem

pi=sum_(k=0)^infty((4+8r)/(8k+1)-(8r)/(8k+2)-(4r)/(8k+3)-(2+8r)/(8k+4)-(1+2r)/(8k+5)-(1+2r)/(8k+6)+r/(8k+7))(1/(16))^k
(55)

pro libovolnou komplexní hodnotu r (Adamčík a Vagón), což dává vzorec BBP jako zvláštní případ r=0.

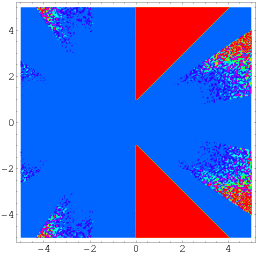
PiFormulasWagonIdentity

Ještě obecnější identita díky Wagonovi je dána vztahem

pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)
(56)

(Borwein a Bailey 2003, p. 141), což platí pro oblast komplexní roviny s výjimkou dvou trojúhelníkových částí symetricky umístěných kolem reálné osy, jak je znázorněno výše.

Snad ještě podivnější obecná třída identit je dána vztahem

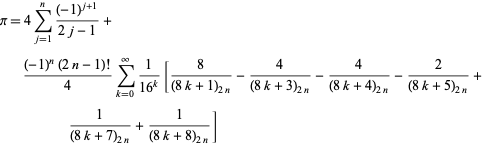pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4sum_(k=0)^infty1/(16^k)
(57)

což platí pro libovolné kladné celé číslo n, kde (x)_n je Pochhammerův symbol (B. Cloitre, pers. comm., 23. ledna 2005). Ještě překvapivější je, že existuje úzce analogický vzorec pro přirozený logaritmus 2.

Po objevu vzorce BBP pro číslice o základu 16 a souvisejících vzorců byly zkoumány podobné vzorce v jiných základech. Borwein, Bailey a Girgensohn (2004) nedávno ukázali, že pi nemá žádnou Machinovu formuli BBP arctangentu, která by nebyla binární, ačkoli to nevylučuje zcela odlišné schéma algoritmů pro extrakci číslic v jiných bázích.

S. Plouffe navrhl algoritmus pro výpočet nčíslice pi v libovolném základu v O(n^3(logn)^3)krocích.

Řadu dalších identit díky Ramanujanovi, Catalanovi a Newtonovi uvádí Castellanos (1988ab, str. 86-88), včetně několika zahrnujících součty Fibonacciho čísel. Ramanujan nalezl

sum_(k=0)^infty((-1)^k(4k+1)^3)/(^3)=sum_(k=0)^infty((-.1)^k(4k+1)^3)/(pi^(3/2)^3)=2/pi
(58)

(Hardy 1923, 1924, 1999, p. 7).

Plouffe (2006) našel krásný vzorec

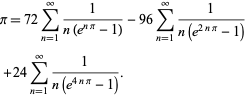pi=72sum_(n=1)^infty1/(n(e^(npi)-1)))-96sum_(n=1)^infty1/(n(e^(2npi)-1))) +24sum_(n=1)^infty1/(n(e^(4npi)-1)).
(59)

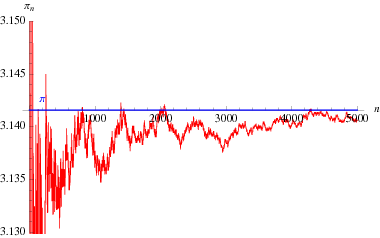
PiBlatnerProduct

Zajímavý vzorec pro nekonečný součin díky Eulerovi, který se týká pi a nprvočísla p_n je

.

pi = 2/(součin_(n=1)^(infty))
(60)
= 2/(součin_(n=2)^(infty))
(61)

(Blatner 1997, p. 119), vynesený výše jako funkce počtu členů v součinu.

K odhadu pi lze použít metodu podobnou Archimédově, a to tak, že začneme s n-úhelníkem a pak vztahujeme plochu následujících 2n-úhelníků. Nechť beta je úhel od středu jedné z úseček mnohoúhelníku,

beta=1/4(n-3)pi,
(62)

tedy

pi=(2sin(2beta))/((n-3)součin_(k=0)^(infty)cos(2^(-k)beta))
(63)

(Beckmann 1989, str. 92-94).

Vieta (1593) jako první uvedl přesný výraz pro pi, když ve výše uvedeném výrazu vzal n=4, čímž získal

cosbeta=sinbeta=1/(sqrt(2))=1/2sqrt(2),
(64)

což vede k nekonečnému součinu vnořenýchradic,

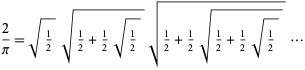2/pi=sqrt(1/2)sqrt(1/2+1/2sqrt(1/2))sqrt(1/2+1/2sqrt(1/2+1/2sqrt(1/2))...
(65)

(Wells 1986, s. 50; Beckmann 1989, s. 95). Konvergenci tohoto výrazu však rigorózně dokázal až Rudio v roce 1892.

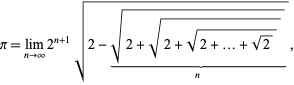
Související vzorec je dán vztahem

pi=lim_(n-infty)2^(n+1)sqrt(2-sqrt(2+sqrt(2+sqrt(2+...+sqrt(2))))_()_(n)),
(66)

což lze zapsat

pi=lim_(n-infty)2^(n+1)pi_n,
(67)

kde pi_n je definováno pomocí iterace

pi_n=sqrt((1/2pi_(n-1))^2+^2)
(68)

s pi_0=sqrt(2) (J. Munkhammar, osobní sdělení, 27. dubna 2000). Vzorec

pi=2lim_(m-infty)sum_(n=1)^msqrt(^2+1/(m^2)).
(69)

také úzce souvisí.

Pěkný vzorec pro pi je dán vztahem

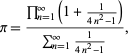pi=(součin_(n=1)^(infty)(1+1/(4n^2-1)))/(součet_(n=1)^(infty)1/(4n^2-1)),
(70)

kde čitatel je forma Wallisova vzorce pro pi/2 a jmenovatel je teleskopický součet se součtem 1/2, protože

1/(4n^2-1)=1/2(1/(2n-1)-1/(2n+1))
(71)

(Sondow 1997).

Zvláštní případ Wallisova vzorce dává

pi/2=produkt_(n=1)^infty=(2-2)/(1-3)(4-4)/(3-5)(6-6)/(5-7)....
(72)

(Wells 1986, s. 50). Tento vzorec lze také zapsat

lim_(n-infty)(2^(4n))/(n(2n; n)^2)=pilim_(n-infty)(n^2)/(^2)=pi,
(73)

kde (n; k) označuje binomický koeficient a Gamma(x) je funkce gama (Knopp 1990). Euler získal

pi=sqrt(6(1+1/(2^2)+1/(3^2)+1/(4^2)+....)),
(74)

což vyplývá ze speciální hodnoty Riemannovy zeta funkce zeta(2)=pi^2/6. Podobné vzorce vyplývají z zeta(2n) pro všechna kladná celá čísla n.

Konečný součet díky Ramanujanovi je

1/pi=sum_(n=0)^infty(2n; n)^3(42n+5)/(2^(12n+4)).
(75)

(Borwein a kol. 1989; Borwein a Bailey 2003, s. 109; Bailey a kol.2007, s. 44). Další součty jsou uvedeny v Ramanujanovi (1913-14),

4/pi=sum_(n=0)^infty((-1)^n(1123+21460n)(2n-1)!!(4n-1)!!)/(882^(2n+1)32^n(n!)^3)
(76)

a

1/pi = sqrt(8)sum_(n=0)^(infty)((1103+26390n)(2n-1)!!(4n-1)!!)/(99^(4n+2)32^n(n!)^3)
(77)
= (sqrt(8))/(9801)sum_(n=0)^(infty)((4n)!(1103+26390n))/((n!)^4396^(4n))
(78)

(Beeler a kol. 1972, položka 139; Borwein a kol. 1989; Borwein a Bailey 2003, s. 108; Bailey a kol. 2007, s. 44). Rovnice (78) je odvozena z modulární identity řádu 58, ačkoli první odvození bylo předloženo až Borweinem a Borweinem (1987). Obě výše uvedené řady dávají

pí přibližně (9801)/(2206sqrt(2))=3,14159273001....
(79)

(Wells 1986, s. 54) jako první přiblížení a poskytují přibližně 6, resp. 8 desetinných míst na člen. Takové řady existují díky racionalitě různých modulárních invariantů.

Obecný tvar řady je

sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)1/(^n)=(sqrt(-j(t)))/pi,
(80)

kde t je diskriminant binární kvadratické formy, j(t) je j-funkce,

.

b(t) = sqrt(t)
(81)
a(t) = (b(t))/6{1-.(E_4(t))/(E_6(t))},
(82)

a E_i jsou Eisensteinovy řady. Pole třídních čísel p zahrnuje pcelá algebraická čísla A=a(t), B=b(t) a C=c(t). Ze všech řad složených pouze z celočíselných členů odpovídá největšímu diskriminantu třídy číslo 1 d=-163 ta, která dává nejvíce číselných znaků za nejkratší dobu a kterou formulovali bratři Chudnovští (1987). Číslo 163, které se zde objevuje, je totéž, které se objevuje v tom, že e^(pisqrt(163)) (Ramanujanova konstanta) je téměř celé číslo. Podobně faktor 640320^3 pochází z identity funkce j pro j(1/2(1+isqrt(163))). Řada je dána vztahem

1/pi = 12sum_(n=0)^(infty)((-1)^n(6n)!(13591409+545140134n))/((n!)^3(3n)!(640320^3)^(n+1/2))
(83)
= (163·8·27·7·11·19·127)/(640320^(3/2))sum_(n=0)^(infty)((13591409)/(163·2·9·7·11·19·127)+n)((6n)!)/((3n)!(n!)^3)((-1)^n)/(640320^(3n))
(84)

(Borwein a Borwein 1993; Beck a Trott; Bailey et al. 2007, s. 44). Tato řada dává 14 číslic přesně na jeden termín. Stejnou rovnici v jiné podobě uvedli bratři Chudnovští (1987) a používá ji jazyk Wolfram k výpočtu pi (Vardi 1991; Wolfram Research),

pi=(426880sqrt(10005))/(A),
(85)

kde

.

A = 13591409
(86)
B = -1/(151931373056000)
(87)
C = (30285563)/(1651969144908540723200).
(88)

Nejlepší vzorec pro třídu číslo 2 (největší diskriminant -427) je

1/pi=12sum_(n=0)^infty((-1)^n(6n)!(A+Bn))/((n!)^3(3n)!C^(n+1/2)),
(89)

kde

.

A = 212175710912sqrt(61)+1657145277365
(90)
B = 13773980892672sqrt(61)+107578229802750
(91)
C = ^3
(92)

(Borwein a Borwein 1993). Tato řada přidává přibližně 25 číslic za každý další člen. Nejrychleji konvergující řada pro třídu číslo 3 odpovídá d=-907 a dává 37-38 číslic na člen. Nejrychleji konvergující řada třídy číslo 4 odpovídá d=-1555 a je

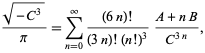(sqrt(-C^3))/pi=sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)(A+nB)/(C^(3n)),
(93)

kde

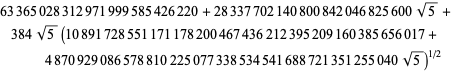A = 63365028312971999585426220+28337702140800842046825600sqrt(5)+384sqrt(5)(10891728551171178200467436212395209160385656017+4870929086578810225077338534541688721351255040sqrt(5))^(1/2)
(94)
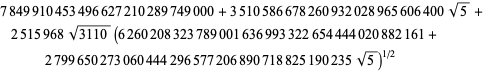B = 7849910453496627210289749000+3510586678260932028965606400sqrt(5)+2515968sqrt(3110)(6260208323789001636993322654444020882161+2799650273060444296577206890718825190235sqrt(5))^(1/2)
(95)
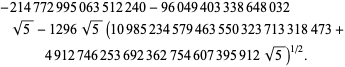C = -214772995063512240-96049403338648032sqrt(5)-1296sqrt(5)(10985234579463550323713318473+4912746253692362754607395912sqrt(5))^(1/2).
(96)

To dává 50 číslic na člen. Borwein a Borwein (1993) vyvinuli obecný algoritmus pro generování takových řad pro libovolné číslo třídy.

Úplný výčet Ramanujanových řad pro 1/pi, které se nacházejí v jeho druhém a třetím sešitě, uvádí Berndt (1994, s. 4 a 5). 352-354),

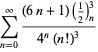4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(97)
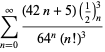(16)/pi = sum_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(98)
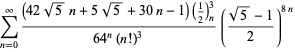(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(99)
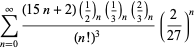(27)/(4pi) = sum_(n=0)^(infty)((15n+2)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(2/(27))^n
(100)
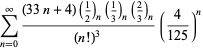(15sqrt(3))/(2pi) = sum_(n=0)^(infty)((33n+4)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(4/(125))^n
(101)
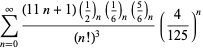(5sqrt(5))/(2pisqrt(3)) = sum_(n=0)^(infty)((11n+1)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(125))^n
(102)
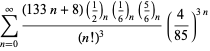(85sqrt(85))/(18pisqrt(3)) = sum_(n=0)^(infty)((133n+8)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(85))^(3n)
(103)
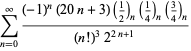4/pi = sum_(n=0)^(infty)((-1)^n(20n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^32^(2n+1))
(104)
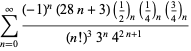4/(pisqrt(3)) = sum_(n=0)^(infty)((-1)^n(28n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^33^n4^(2n+1))
(105)
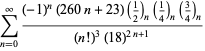4/pi = sum_(n=0)^(infty)((-1)^n(260n+23)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(18)^(2n+1))
(106)
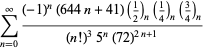4/(pisqrt(5)) = sum_(n=0)^(infty)((-1)^n(644n+41)(1/2)_n(1/4)_n(3/4)_n)/((n!)^35^n(72)^(2n+1))
(107)
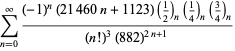4/pi = sum_(n=0)^(infty)((-1)^n(21460n+1123)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(882)^(2n+1))
(108)
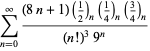(2sqrt(3))/pi = sum_(n=0)^(infty)((8n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^n)
(109)
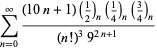1/(2pisqrt(2)) = sum_(n=0)^(infty)((10n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^(2n+1))
(110)
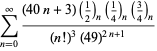1/(3pisqrt(3)) = sum_(n=0)^(infty)((40n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(49)^(2n+1))
(111)
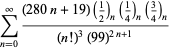2/(pisqrt(11)) = sum_(n=0)^(infty)((280n+19)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(2n+1))
(112)
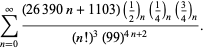1/(2pisqrt(2)) = sum_(n=0)^(infty)((26390n+1103)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(4n+2)).
(113)

Tyto rovnice poprvé dokázali Borwein a Borwein (1987a, s. 177-187). Borwein a Borwein (1987b, 1988, 1993) dokázali další rovnice tohoto typu a Chudnovsky a Chudnovsky (1987) našli podobné rovnice pro jiné transcendentální konstanty (Bailey et al. 2007, s. 44-45).

Úplný seznam nezávislých známých rovnic tohoto typu je dán

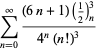4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(114)
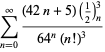(16)/pi = sum_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(115)
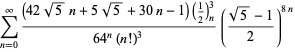(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(116)
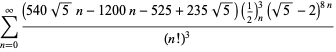(5^(1/4))/pi = sum_(n=0)^(infty)((540sqrt(5)n-1200n-525+235sqrt(5))(1/2)_n^3(sqrt(5)-2)^(8n))/((n!)^3)
(117)
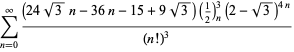(12^(1/4))/pi = sum_(n=0)^(infty)((24sqrt(3)n-36n-15+9sqrt(3))(1/2)_n^3(2-sqrt(3))^(4n))/((n!)^3)
(118)

pro m=1 s nestejnými znaménky,

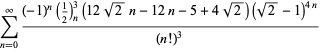2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(12sqrt(2)n-12n-5+4sqrt(2))(sqrt(2)-1)^(4n))/((n!)^3)
(119)
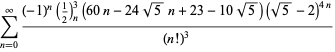2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(60n-24sqrt(5)n+23-10sqrt(5))(sqrt(5)-2)^(4n))/((n!)^3)
(120)
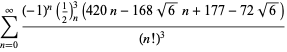2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(420n-168sqrt(6)n+177-72sqrt(6)))/((n!)^3)
(121)
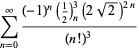(2sqrt(2))/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(2sqrt(2))^(2n))/((n!)^3)
(122)

pro m=1 se střídavými znaménky,

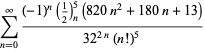(128)/(pi^2) = součet_(n=0)^(infty)((-1)^n(1/2)_n^5(820n^2+180n+13))/(32^(2n)(n!)^5)
(123)
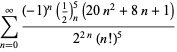(32)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(20n^2+8n+1))/(2^(2n)(n!)^5)
(124)

pro m=2 (Guillera 2002, 2003, 2006),

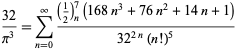(32)/(pi^3)=sum_(n=0)^infty((1/2)_n^7(168n^3+76n^2+14n+1))/(32^(2n)(n!)^5)
(125)

pro m=3 (Guillera 2002, 2003, 2006) a žádné další pro m3 nejsou známy (Bailey et al. 2007, s. 45-48).

Bellard uvádí exotický vzorec

pi=1/(740025),
(126)

where

P(n)=-885673181n^5+3125347237n^4-2942969225n^3+1031962795n^2-196882274n+10996648.
(127)

Gasper uvádí výsledek

pi=(16)/3^(-1),
(128)

kde _1F_2 je zobecněná hypergeometrická funkce, a transformuje ji na

pi=lim_(x-infty)4x_1F_2(1/2;3/2,3/2;-x^2).
(129)

Fascinující výsledek díky Gosperovi je dán

lim_(n-infty)součin_(i=n)^(2n)pi/(2tan^(-1)i)=4^(1/pi)=1,554682275.....
(130)

pi splňuje nerovnost

(1+1/pi)^(pi+1) cca 3,14097pi.
(131)

D. Terr (pers. comm.) zaznamenal zvláštní identitu

(3,1,4)=(1,5,9)+(2,6,5) (mod 10)
(132)

zahrnující prvních 9 číslic pí.

.

Napsat komentář

Vaše e-mailová adresa nebude zveřejněna.