
Matematik omhandler et enormt antal begreber, som er meget vigtige, men samtidig komplekse og tidskrævende. Python tilbyder dog det fuldgyldige SciPy-bibliotek, der løser dette problem for os. I denne SciPy-tutorial lærer du, hvordan du kan gøre brug af dette bibliotek sammen med et par funktioner og deres eksempler.
Hvor du går videre, skal du tage et kig på alle de emner, der er behandlet i denne artikel:
- Hvad er SciPy?
- NumPy vs. SciPy
- Underpakker i SciPy
- Basisfunktioner
- Speciale funktioner
- Integrationsfunktioner
- Optimeringsfunktioner
- Fouriertransformationsfunktioner
- Signal Processing Functions
- Sparse egenværdier
- Spatial Data Structures and Algorithms
- Multidimensional Image Processing Functions
- File IO
Linear Algebra
Så lad os komme i gang. 🙂
SciPy er et Python-bibliotek med åben kildekode, som bruges til at løse videnskabelige og matematiske problemer. Det er bygget på NumPy-udvidelsen og giver brugeren mulighed for at manipulere og visualisere data med en bred vifte af kommandoer på højt niveau. Som tidligere nævnt bygger SciPy på NumPy, og hvis du importerer SciPy, er det derfor ikke nødvendigt at importere NumPy.
NumPy vs SciPy
Både NumPy og SciPy er Python-biblioteker, der bruges til brugt matematisk og numerisk analyse. NumPy indeholder array-data og grundlæggende operationer såsom sortering, indeksering osv., mens SciPy består af al den numeriske kode. Selvom NumPy indeholder en række funktioner, der kan hjælpe med at løse lineær algebra, Fouriertransformationer osv., er SciPy det bibliotek, der faktisk indeholder fuldt udbyggede versioner af disse funktioner sammen med mange andre. Hvis du laver videnskabelige analyser med Python, skal du dog installere både NumPy og SciPy, da SciPy bygger på NumPy.
Underpakker i SciPy:
SciPy har en række underpakker til forskellige videnskabelige beregninger, som er vist i følgende tabel:

For en detaljeret beskrivelse kan du dog følge den officielle dokumentation.
Disse pakker skal udelukkende importeres, før de kan bruges. For eksempel:
from scipy import cluster
Hvor vi ser nærmere på hver af disse funktioner, skal vi først se på de funktioner, der er fælles både i NumPy og SciPy.
Interaktion med NumPy:
SciPy bygger på NumPy, og derfor kan du selv gøre brug af NumPy-funktioner til at håndtere arrays. Hvis du vil vide mere om disse funktioner i dybden, kan du blot gøre brug af funktionerne help(), info() eller source().
help():
For at få oplysninger om en hvilken som helst funktion kan du gøre brug af funktionen help(). Der er to måder, hvorpå denne funktion kan bruges:
- uden parametre
- med parametre
Her er et eksempel, der viser begge ovenstående metoder:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Når du udfører ovenstående kode, returnerer den første help() oplysningerne om cluster-submodulet. Den anden help() beder brugeren om at indtaste navnet på et modul, et nøgleord osv. som brugeren ønsker at søge oplysninger om. Hvis du vil stoppe udførelsen af denne funktion, skal du blot skrive “quit” og trykke på enter.
info():
Denne funktion returnerer oplysninger om de ønskede funktioner, moduler osv..
scipy.info(cluster)
source():
Kildekoden returneres kun for objekter, der er skrevet i Python. Denne funktion returnerer ikke nyttige oplysninger, hvis metoderne eller objekterne er skrevet i et andet sprog som f.eks. C. Hvis du imidlertid ønsker at gøre brug af denne funktion, kan du gøre det på følgende måde:
scipy.source(cluster)
Speciale funktioner:
SciPy indeholder en række specielle funktioner, der bruges i matematisk fysik som f.eks. elliptiske, bekvemmelighedsfunktioner, gamma, beta osv. For at søge efter alle funktionerne kan du gøre brug af funktionen help() som beskrevet tidligere.
Exponential- og trigonometriske funktioner:
SciPys pakke Special Function indeholder en række funktioner, hvorigennem du kan finde eksponenter og løse trigonometriske problemer.
Se på følgende eksempel:
EXEMPEL:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
OUTPUT:
1000.0
8.0
1.0
1.0
0.7071067811865475
Der er mange andre funktioner til stede i SciPys specielle funktionspakke, som du selv kan prøve.
Integrationsfunktioner:
SciPy indeholder en række funktioner til at løse integraler. Lige fra almindelig differentiel integrator til brug af trapezregler til beregning af integraler er SciPy et lager af funktioner til løsning af alle typer integralproblemer.
Generel integration:
SiPy indeholder en funktion ved navn quad til beregning af integralet af en funktion, der har én variabel. Grænserne kan være ( ) for at angive uendelige grænser. Syntaksen for funktionen quad() er som følger:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Her vil funktionen blive integreret mellem grænserne a og b (kan også være uendelig).
EKSEMPEL:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
I ovenstående eksempel evalueres funktionen “a” mellem grænserne 0, 1. Når denne kode udføres, vil du se følgende output.
OUTPUT:
(3.9086503371292665, 4.3394735994897923e-14)
Dobbeltintegralfunktion:
SciPy indeholder dblquad, der kan bruges til at beregne dobbeltintegraler. Et dobbeltintegral består, som mange af os ved, af to reelle variabler. Funktionen dblquad() tager den funktion, der skal integreres, som parameter sammen med 4 andre variabler, som definerer grænserne og funktionerne dy og dx.
EXEMPEL:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
OUTPUT:
-1.33333333333333333335, 1.4802973661668755e-14)
SciPy indeholder forskellige andre funktioner til evaluering af tredobbelte integraler, n-integraler, Romberg-integraler osv. som du kan udforske yderligere i detaljer. Du kan finde alle detaljer om de nødvendige funktioner ved at bruge hjælpefunktionen.
Optimeringsfunktioner:
Scipy.optimize indeholder en række almindeligt anvendte optimeringsalgoritmer, som kan ses ved hjælp af hjælpefunktionen.
Den består grundlæggende af følgende:
- Ubundet og begrænset minimering af multivariate skalarfunktioner dvs. minimere (f.eks. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, osv.)
- Globale optimeringsrutiner (f.eks. differential_evolution, dual_annealing, osv)
- Mindste kvadraters minimering og kurvetilpasning (f.eks. least_squares, curve_fit, osv)
- Skalare univariate funktioner minimeringsværktøjer og rodfindere (f.eks. minimize_scalar og root_scalar)
- Multivariat ligningssystemløsere ved hjælp af algoritmer som f.eks. hybrid Powell, Levenberg-Marquardt.
Rosenbrook-funktion:
Rosenbrook-funktion ( rosen) er et testproblem, der anvendes til gradientbaserede optimeringsalgoritmer. Den er defineret som følger i SciPy:

EXEMPEL:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
OUTPUT: 7371.039999999999945
Nelder-Mead:
Nelder-Mead-metoden er en numerisk metode, der ofte anvendes til at finde min/max for en funktion i et flerdimensionalt rum. I det følgende eksempel anvendes minimere-metoden sammen med Nelder-Mead-algoritmen.
EXEMPEL:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
OUTPUT: array()
Interpolationsfunktioner:
I numerisk analyse henviser interpolation til konstruktion af nye datapunkter inden for et sæt af kendte datapunkter. SciPy-biblioteket består af en underpakke ved navn scipy.interpolate, der består af spline-funktioner og -klasser, endimensionale og flerdimensionale (univariate og multivariate) interpolationsklasser osv.
Univariate interpolation:
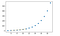
Univariate interpolation er grundlæggende et område inden for kurvepasning, som finder den kurve, der giver en nøjagtig tilpasning til en serie af todimensionale datapunkter. SciPy indeholder interp1d-funktionen, der kan udnyttes til at producere univariat interpolation.
EKSEMPEL:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
OUTPUT:
Multivariat interpolation:
Multivariat interpolation (rumlig interpolation ) er en slags interpolation på funktioner, der består af mere end én variabel. Følgende eksempel viser et eksempel på
Interpolering over et 2-D gitter ved hjælp af funktionen interp2d(x, y, z) vil grundlæggende bruge x, y, z arrays til at tilnærme sig en eller anden funktion interp2d funktion. f: “z = f(x, y)” og returnerer en funktion, hvis kaldsmetode bruger splineinterpolation til at finde værdien af nye punkter.
EKSEMPEL:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
OUTPUT:

Fouriertransformationsfunktioner:
Fourieranalyse er en metode, der handler om at udtrykke en funktion som en sum af periodiske komponenter og genvinde signalet ud fra disse komponenter. FFT-funktionerne kan bruges til at returnere den diskrete Fouriertransformation af en reel eller kompleks sekvens.
EKSEMPEL:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
OUTPUT:
På samme måde kan du finde den inverse af dette ved at bruge ifft-funktionen på følgende måde:
EKSEMPEL:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
OUTPUT:
Signalbehandlingsfunktioner:
Signalbehandling beskæftiger sig med at analysere, ændre og syntetisere signaler som f.eks. lyd, billeder osv. SciPy indeholder nogle funktioner, hvormed du kan designe, filtrere og interpolere endimensionale og todimensionale data.
Filtrering:
Gennem at filtrere et signal fjerner du grundlæggende uønskede komponenter fra det. For at udføre ordnet filtrering kan du gøre brug af funktionen order_filter. Denne funktion udfører grundlæggende en ordnet filtrering på et array. Syntaksen for denne funktion er som følger:
SYNTAX:
order_filter(a, domain, rank)
a = N-dimensionelt input array
domain = maske array med samme antal dimensioner som `a`
rank = Ikke-negativt tal, der udvælger elementer fra listen, efter at den er blevet sorteret (0 er det mindste efterfulgt af 1…)
EXEMPEL:
from scipy import signal
x = np.arange(35).reshape(7, 5)
domain = np.identity(3)
print(x,end='nn')
print(signal.order_filter(x, domain, 1))
OUTPUT:
]
]
Waveforms:
The scipy.signal-underpakke består også af forskellige funktioner, der kan bruges til at generere bølgeformer. En af disse funktioner er chirp. Denne funktion er en frekvens-swept cosinusgenerator, og syntaksen er som følger:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
hvor,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
OUTPUT:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)

Linær algebra:
Linær algebra beskæftiger sig med lineære ligninger og deres repræsentationer ved hjælp af vektorrum og matricer. SciPy er bygget på ATLAS LAPACK- og BLAS-bibliotekerne og er ekstremt hurtig til at løse problemer i forbindelse med lineær algebra. Ud over alle funktionerne fra numpy.linalg indeholder scipy.linalg også en række andre avancerede funktioner. Hvis numpy.linalg ikke anvendes sammen med ATLAS LAPACK- og BLAS-understøttelse, er scipy.linalg også hurtigere end numpy.linalg.
Finding the Inverse of a Matrix:
Matematisk set er inversen af en matrix A den matrix sådan, at hvor er identitetsmatrixen bestående af ettere ned langs hoveddiagonalen betegnet som B=A-1. I SciPy kan denne inverse fås ved hjælp af linalg.inv-metoden.
EXEMPEL:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
OUTPUT:
]
Finding the Determinants:
Den værdi, der aritmetisk udledes af matrixens koefficienter, kaldes determinanten for en kvadratisk matrix. I SciPy kan dette gøres ved hjælp af en funktion det, der har følgende syntaks:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
hvor,
a : (M, M) Er en kvadratisk matrix
overwrite_a( bool, valgfrit) : Tillader overskrivning af data i a
check_finite ( bool, valgfrit): For at kontrollere, om inputmatrixen kun består af finitte tal
EXEMPEL:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
OUTPUT: -5.0
Sparse egenværdier:
Egenværdier er et specifikt sæt af skalarer, der er forbundet med lineære ligninger. ARPACK giver, der gør det muligt at finde egenværdier ( egenvektorer ) ret hurtigt. Den komplette funktionalitet i ARPACK er pakket i to grænseflader på højt niveau, som er scipy.sparse.linalg.eigs og scipy.sparse.linalg.eigsh. eigs. Grænsefladen eigs gør det muligt at finde egenværdierne for reelle eller komplekse ikke-symmetriske kvadratiske matricer, mens grænsefladen eigsh indeholder grænseflader for reelle symmetriske eller komplekse hermitiske matricer.
Funktionen eigh løser et generaliseret egenværdiproblem for en kompleks hermitisk eller reel symmetrisk matrix.
EXEMPEL:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
OUTPUT:
Selected eigenvalues :
Kompleks ndarray :
]
Spatiale datastrukturer og algoritmer:
Spatiale data består grundlæggende af objekter, der består af linjer, punkter, overflader osv. Pakken scipy.spatial i SciPy kan beregne Voronoi-diagrammer, trianguleringer osv. ved hjælp af Qhull-biblioteket. Den består også af KDTree-implementeringer til forespørgsler om nærmeste nabo punkt.
Delaunay-trianguleringer:
Matematisk set er Delaunay-trianguleringer for et sæt af diskrete punkter i et plan en sådan triangulering, at intet punkt i det givne sæt af punkter ligger inden for omkredsen af nogen af trekanterne.
EKSEMPEL:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
UDGANG:

Multidimensionale billedbehandlingsfunktioner:
Billedbehandling handler grundlæggende om at udføre operationer på et billede for at hente oplysninger eller for at få et forbedret billede ud fra det oprindelige billede. Pakken scipy.ndimage består af en række billedbehandlings- og analysefunktioner, der er designet til at arbejde med arrays af vilkårlig dimensionalitet.
Konvolution og korrelation:
SciPy indeholder en række funktioner, der muliggør korrelation og konvolution af billeder.
- Funktionen correlate1d kan bruges til at beregne endimensional korrelation langs en given akse
- Funktionen correlate tillader flerdimensional korrelation af et givet array med den angivne kerne
- Funktionen convolve1d kan bruges til at beregne en-dimensionel konvolution langs en given akse
Funktionen convolve muliggør flerdimensionel konvolution af et givet array med den angivne kerne
EKSEMPEL:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
Fil IO:
Den scipy.io-pakken indeholder en række funktioner, der hjælper dig med at håndtere filer i forskellige formater, f.eks. MATLAB-filer, IDL-filer, Matrix Market-filer osv.
For at gøre brug af denne pakke skal du importere den som følger:
import scipy.io as sio
For fuldstændige oplysninger om underpakken kan du se det officielle dokument om File IO.
Det bringer os til slutningen af denne SciPy-vejledning. Jeg håber, at du har forstået alt klart og tydeligt. Sørg for at øve dig så meget som muligt.
Hvis du ønsker at tjekke flere artikler om markedets mest trending teknologier som kunstig intelligens, DevOps, Ethical Hacking, så kan du henvise til Edurekas officielle websted.
Du skal holde øje med andre artikler i denne serie, som vil forklare de forskellige andre aspekter af Python og Data Science.
1. Machine Learning Classifier in Python
2. Python Scikit-Learn Cheat Sheet
3. Machine Learning Tools
4. Python Libraries For Data Science And Machine Learning
5. Chatbot In Python
6. Python Collections
7. Python Modules
8. Python developer Skills
9. Python developer Skills
9. OOPs Interview spørgsmål og svar
10. Resume for en Python-udvikler
11. Exploratory Data Analysis In Python
12. Slangespil med Pythons skildpaddemodul
13. Python Developer Salary
14. Hovedkomponentanalyse
15. Python vs C++
16. Scrapy Tutorial
17. Webscraping med Python
18. Regressionsmetode med mindste kvadraters regression
19. Jupyter Notebook Cheat Sheet
20. Python-grundlæggende principper
21. Python-mønsterprogrammer
22. Generatorer i Python
23. Python Decorator
24. Python Spyder IDE
25. Mobile applikationer ved hjælp af Kivy i Python
26. Top 10 bedste bøger til at lære & øv Python
27. Robot Framework Med Python
28. Slangespil i Python ved hjælp af PyGame
29. Django-interviewspørgsmål og svar
30. Top 10 Python-applikationer
31. Hashtabeller og Hashmaps i Python
32. Python 3.8
33. Supportvektormaskine
34. Vejledning i Python