
Neuronale Netze und Mathematik sind untrennbar miteinander verbunden, und das ist es wahrscheinlich, was den meisten Menschen Angst macht. Ich habe schon zu viele zweifelhafte Bemerkungen über Deep Learning gehört: „Das ist mir zu viel Mathe“, „Wie viele Unternehmen nutzen Deep Learning wirklich? Ich erspare mir lieber das Kopfzerbrechen und halte mich von diesen anspruchsvollen Konzepten fern.“
Aber wenn man darüber nachdenkt, ist es gar nicht so schwierig. Glauben Sie mir! Um zu verstehen, warum sich ein Algorithmus auf eine bestimmte Art und Weise verhält, ist es wichtig zu verstehen, was hinter den Kulissen passiert. Komplexe Algorithmen des maschinellen Lernens sind heute für uns bequem verpackt und nur einen Funktionsaufruf entfernt. Die Ableitungen von Aktivierungsfunktionen sind etwas weniger offensichtliche Konzepte, die wir oft zu ignorieren pflegen. Sie bilden jedoch die Grundlage leistungsfähiger Algorithmen, und es lohnt sich auf jeden Fall, sich ein wenig mehr Mühe zu geben, um sie zu verstehen. Nach der Lektüre dieses Artikels werden Sie einen Schritt weiter sein, um zu enträtseln, was sich hinter der Fassade der „Black Box“ verbirgt.
Hintergrund
Neuronale Netze verwenden eine Vielzahl von Aktivierungsfunktionen in den versteckten und den Ausgabeschichten, um den Lernprozess zu katalysieren. Zu den häufig verwendeten Aktivierungsfunktionen gehören die Sigmoid- und die tanH-Funktion. Die beliebteste Aktivierungsfunktion ist die ReLU-Funktion (Rectified Linear Unit), da sie das Problem des verschwindenden Gradienten effektiv lösen kann. Ein tieferer Einblick in Aktivierungsfunktionen ist ein Thema für einen anderen Tag. Heute werden wir uns auf die Mathematik hinter der Ableitung der Sigmoid-Funktion konzentrieren.
Warum ist die Ableitung einer Aktivierungsfunktion wichtig?
Wie Sie wahrscheinlich wissen, werden neuronale Netze in zwei Schritten gesteuert:
- Vorwärtspropagation – Die Eingabedaten fließen durch das Netz und wir erhalten die vorhergesagte Ausgabe. Wir vergleichen sie mit der tatsächlichen Ausgabe und berechnen den Fehler.
- Back Propagation – Der berechnete Fehler wird verwendet, um die Parameter des neuronalen Netzes mit Hilfe der Ableitung der Aktivierungsfunktion zu aktualisieren.
Die Sigmoidfunktion
Die Sigmoidfunktion, die durch eine S-förmige Kurve gekennzeichnet ist, wird oft als ein Spezialfall der logistischen Funktion bezeichnet. Sie ist am nützlichsten in Fällen, in denen wir die Wahrscheinlichkeit als Ausgabe vorhersagen müssen.
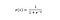
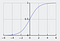
Die Sigmoidfunktion gibt Werte aus, die zwischen 0 und 1 liegen (zu Recht, denn sie sagt Wahrscheinlichkeiten voraus).
Die Sigmoidableitung
Dieser grundlegende Baustein, der beim Training neuronaler Netze hilft, hat die Form:


Schnell und einfach, Lasst uns die Ableitung in Angriff nehmen!
Ansatz 1

Ansatz 2:
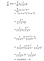
Warum verwenden wir diese Version der Ableitung?
Im Vorwärtspropagationsschritt wird die Sigmoidfunktion (σ(x)) berechnet und ihr Wert zur Verfügung gestellt. Bei der Berechnung der Ableitung im Backpropagation-Schritt muss man nur den Wert von σ(x) in die oben abgeleitete Formel einsetzen und voila, man ist startklar!
Das war’s, Leute! Danke fürs Lesen!