Vaihtovirta eli vaihtovirta on saanut nimensä siksi, että virta vaihtuu tai vaihtuu edestakaisin kahden napaisuuden välillä. Toisin sanoen virta (ja siten myös jännite) on ajan funktio. Tämä eroaa olennaisesti tasavirrasta, jonka napaisuus on kiinteä ja yleensä vakio ajan kuluessa. Esimerkiksi laboratorion tasajännitelähde säilyttää ihanteellisessa tapauksessa kiinteän jännitteen liittimissään eikä se muutu ajan mittaan. Sitä vastoin, kun vaihtovirta-aaltomuoto heilahtaa edestakaisin ajassa, sen muoto voi vaihdella laajalti laboratoriostandardien yksinkertaisista, säännöllisistä poluista, kuten siniaalloista, kolmioaalloista ja neliöaalloista, paljon monimutkaisempiin ja aaltoileviin aaltomuotoihin, joita musiikkisoittimet ja ihmisääni tuottavat.
Siniaalto on yksinkertaisin aalto, joka voidaan luoda. Se edustaa vakionopeudella pyörivän yksinkertaisen vektorin liikettä, kuten kellon sekuntiosoittimen pystysuuntaista siirtymää. Esimerkki on esitetty kuvassa \(\PageIndex{1}\). Vaaka-akselille on piirretty aika. Se kasvaa siirryttäessä vasemmalta oikealle (eli jos piste A on pisteen B oikealla puolella, piste A on ajassa myöhemmin kuin piste B). Pystyakseli esitetään tässä yleisesti prosenttiosuutena maksimista, mutta tavallisesti se olisi jännitteen, virran, äänenpaineen tai vastaavan mittaus.
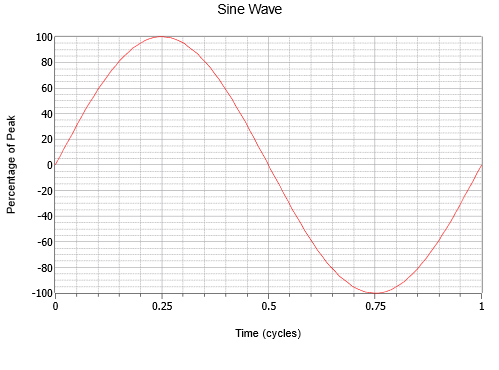
Kuvio \(\PageIndex{1}\): Siniaalto.
Huomaa tasainen vaihtelu, joka alkaa nollasta, nousee positiiviseen piikkiin neljänneksen matkalla, laskee takaisin nollaan puolivälissä, jatkuu negatiiviseen piikkiin kolmen neljänneksen matkalla ja nousee sitten taas siihen, mistä se alkoi. Sitten tämä prosessi toistuu. Jokaista toistoa kutsutaan sykliksi. Kuvassa \(\PageIndex{1}\) on esitetty yksi kokonainen sykli.
Siniaalloilla on neljännesaaltosymmetria. Toisin sanoen aallon jokainen neljännes (ajallisesti) on identtinen minkä tahansa muun aallon kanssa, jos sitä vain käännetään vaaka-akselin ympäri ja/tai käännetään pystysuoraan huippunsa ympäri. Yhden syklin kestoa kutsutaan jaksoksi, ja sitä merkitään symbolilla \(T\) (= aika). Jakson käänteisluku on taajuus, \(f\).
\
Taajuus kertoo, kuinka monta sykliä yhdessä sekunnissa on. Yhden 1800-luvun alan tutkijan kunniaksi käytämme yksikköä ”sykliä sekunnissa” sen sijaan, että kutsuisimme sitä nimellä ”syklit sekunnissa”, Hertz, joka on nimetty Heinrich Hertzin mukaan ja josta käytetään lyhennettä Hz. Kuvassa \(\PageIndex{2}\) esitetään kolme siniaaltoa eri taajuuksilla; alkuperäinen aalto (vihreä), aalto, jonka taajuus on kaksinkertainen (sininen), ja kolmas aalto, jonka taajuus on puolet taajuudesta tai kaksi kertaa jakso (punainen).
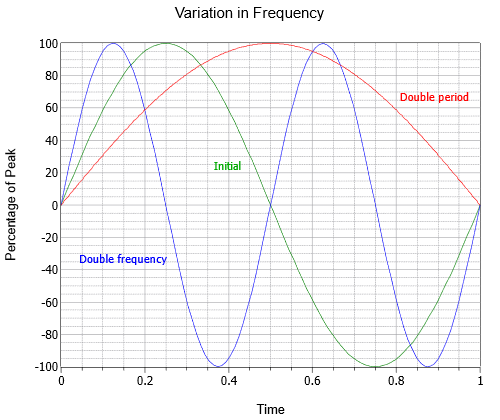
Kuva \(\PageIndex{2}\): Siniaallon taajuuden vaihtelu.
Aallon amplitudi (pystysuora) voidaan ilmaista huippusuuruutena, joka on muutos keskimmäisestä nollaviivasta positiivisimpaan arvoon asti. Amplitudi voidaan ilmaista myös peak-to-peak-määränä; etäisyys negatiivisimmasta positiivisimpaan arvoon. Siniaallolle tämä on aina kaksinkertainen huippuarvoon nähden, vaikka tämä ei välttämättä pidä paikkaansa muiden aaltojen kohdalla, jotka voivat olla epäsymmetrisiä. Kuvassa \(\PageIndex{3}\) on esitetty sarja kolmea siniaaltoa, joiden amplitudit eroavat toisistaan. Alkuperäisen (vihreä) rinnalla on kaksinkertaisen amplitudin (sininen) ja puolen amplitudin (punainen) versiot.
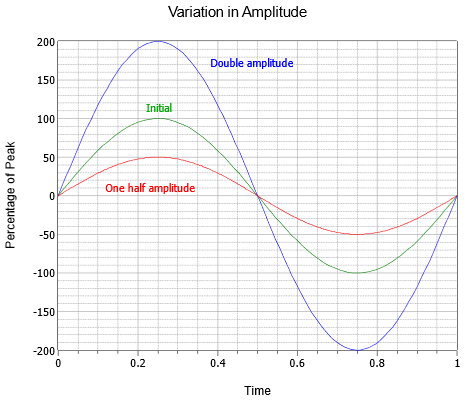
Kuva \(\PageIndex{3}\): Siniaallon amplitudin vaihtelu.
Yhdistämällä nämä parametrit tarkastellaan kuvassa \(\PageIndex{4}\) esitettyä jännitteen aaltomuotoa. Tässä nähdään vaihtojännitteen aaltomuodon kaksi jaksoa.
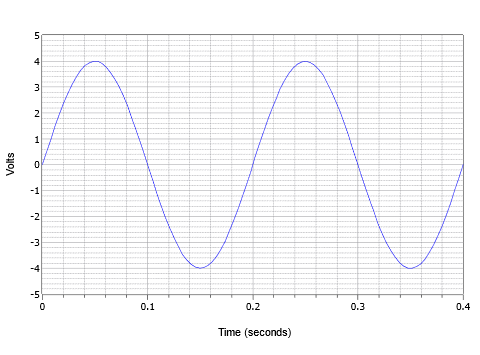
Kuva \(\PageIndex{4}\): Esimerkki siniaallon perusmuodosta.
Huippuarvo on 4 volttia ja huipusta huippuun -arvo on 8 volttia (tyypillisesti lyhenne ”8 V pp”). Yhden jakson jakso on 0,2 sekuntia eli \(T = 200\) millisekuntia. Lisäksi taajuus on \(f = 1/200\) millisekuntia eli 5 Hz (5 sykliä sekunnissa).
Vaihtovirta-aaltomuodot voidaan myös yhdistää tasavirtaoffsetin kanssa. Positiivisen DC-tason lisääminen siirtää aaltoa pystysuunnassa ylöspäin, kun taas negatiivinen DC-taso siirtää aaltoa pystysuunnassa alaspäin. Tämä ei muuta taajuutta tai amplitudin AC-osaa (vaikka absoluuttiset huiput siirtyisivät DC-arvon verran). Kuvassa \(\PageIndex{5}\) esitetään erilaisten tasavirtapoikkeamien vaikutus. Alkuperäisen aallon (vihreä) yläpuolella on muuten identtinen aalto, jonka positiivinen DC-offset on 20 % alkuperäisestä huippuarvosta (sininen). Alkuperäisen aallon alapuolella on kolmas aalto (punainen), jonka negatiivinen DC-offset on puolet alkuperäisen aallon huippuarvosta.
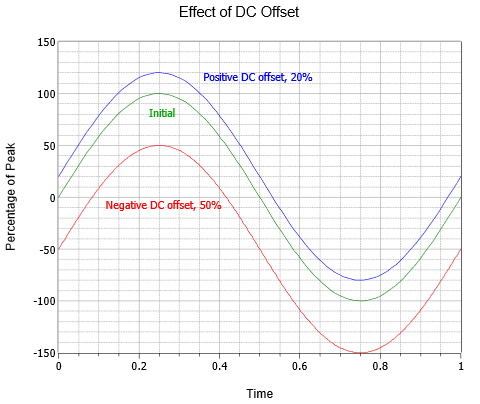
Kuva \(\PageIndex{5}\): Siniaallon DC-offsetin vaihtelu.
Myös on mahdollista, että siniaalto on ajallisesti siirtynyt verrattuna johonkin toiseen siniaaltoon tai referenssiin. Vaikka tämä siirtymä on mahdollista ilmoittaa absoluuttisena aikana, on tavallisempaa ilmoittaa se vaihesiirtymänä, eli aika ilmaistuna jakson osuutena asteina. Jos esimerkiksi yksi sini on edellä toista neljännesjakson verran, sen sanotaan olevan edellä 90\(^{\circ}\) (eli 1/4 360\(^{\circ}\)). Jos se on jäljessä ½ jaksosta, sen sanotaan olevan jäljessä 180\(^{\circ}\) (eli 1/2 jaksoa myöhemmin). Toinen tapa ilmaista tämä on, että johtavat aaltomuodot alkavat aikaisemmin ajassa ja piirtyvät siten viitteestä vasemmalle, kun taas jäljessä olevat aaltomuodot alkavat myöhemmin ajassa ja piirtyvät oikealle.
Kuvassa \(\PageIndex{6}\) on havainnollistettu vaiheensiirron vaikutusta. Huomaa, että tässä kuvaajassa \(t = 0\) on siirretty vaaka-akselin keskelle. Keskimmäinen käyrä on alkuperäinen eli viiteaalto (vihreä). Vasemmalla (punainen) on aalto, joka johtaa alkuperäistä aaltoa yhden kahdeksasosajakson verran eli 45\(^{\circ}\). Oikealla (sininen) on aalto, joka on jäljessä puolet vähemmän eli -22.5\(^{\circ}\).
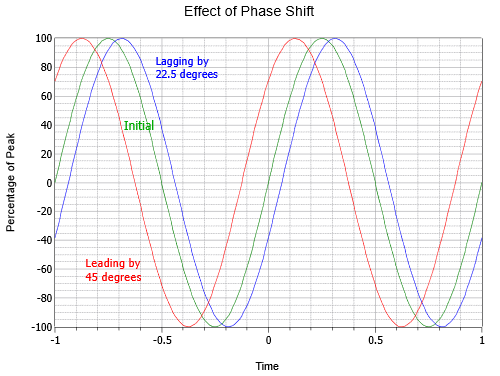
Kuvio \(\PageIndex{6}\): Siniaallon vaiheen vaihtelu.
Edellisten elementtien yhdistämisen avulla voimme kehittää yleisen muodon siniaallolle (kuvassa jännite):
\
Missä
\(v(t)\) on jännite jollakin hetkellä \(t\),
\(V_{DC}\) on mahdollinen DC-offset,
\(V_{P}\) on huippuarvo,
\(f\) on taajuus,
\(\theta\) on vaihesiirtymä (+, jos edellä ja vasemmalle piirretty, – jos jäljessä ja oikealle piirretty).
Nopean ja käytännöllisen esimerkin vuoksi kuvassa \(\PageIndex{4}\) esitetyn aaltomuodon amplitudi on 4 volttia huipussaan, taajuus on 5 Hz eikä siinä ole DC-offsetia tai vaihesiirtoa. Näin ollen sen lauseke on \(v(t) = 4 \sin (2 \pi 5 t)\)
Vaihesiirron laskemiseksi määritetään ensin aaltomuodon ja referenssin välinen aikaero, jota kutsutaan nimellä \(\Delta t\). Referenssi voi olla kiinteä aikapiste (esim. \(t = 0\)) tai toinen aaltomuoto. Yleensä helppo tapa tehdä tämä on mitata ero nollakohdan ylityksissä olettaen, että DC-offsetia ei ole. Jos offset on olemassa, tee mittaus, johon nollakohta on siirtynyt (eli DC-offset-tasolle). Kun ero on löydetty, jaa se jaksolla, jotta siirtymä voidaan esittää jakson murto-osana. Koska yksi jakso vastaa yhtä vektorin kierrosta eli 360 astetta, kerro yksinkertaisesti murto-osa 360 asteella, jotta saadaan vaihesiirtymä asteina. Kaavalla ilmaistuna:
\
Muista, että jos aalto on siirtynyt vasemmalle, se on etenevä ja positiivinen, kun taas siirtymä oikealle on viiveinen tai viivästynyt ajassa ja siten negatiivinen.
Esimerkki \(\PageIndex{1}\)
Kirjoita lauseke kuvassa \(\PageIndex{7}\) esitetylle aaltomuodolle.
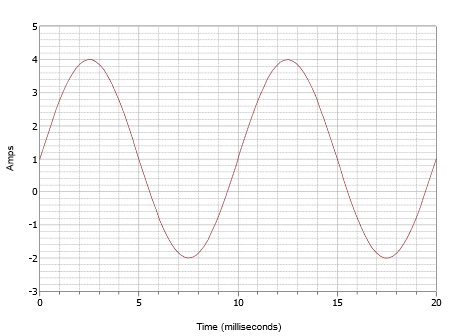
Kuvassa \(\PageIndex{7}\): Esimerkin \(\PageIndex{1}\) aaltomuoto.
Tämä aaltomuoto saattaa pinnallisesti näyttää samalta kuin kuvassa \(\PageIndex{4}\), mutta älä anna tämän hämätä. Ensinnäkin aika-asteikko on erilainen. Tässä aaltomuodossa yksi sykli kestää 10 millisekuntia. Siksi taajuus on
\
\
\
\
Toinen ongelma on DC-offset. Huomaa, että positiivinen huippu esiintyy 4 ampeerin kohdalla, kun taas negatiivinen huippu esiintyy -2 ampeerin kohdalla. Tämä osoittaa, että huipun ja huipun välinen arvo on 6 ampeeria. Ilman offsetia positiivinen huippu olisi 3 ampeeria, joten DC-offset on +1 ampeeria. Aaltomuodon pystysuora keskipiste on siirtynyt ylöspäin 0 ampeerista +1 ampeeriin. Tämä piste on kohdassa t = 0, joten vaihesiirtoa ei tapahdu. Tuloksena saatava lauseke on:
\
Esimerkki \(\PageIndex{2}\)
Kirjoita lauseke kuvassa \(\PageIndex{8}\) esitetylle aaltomuodolle.
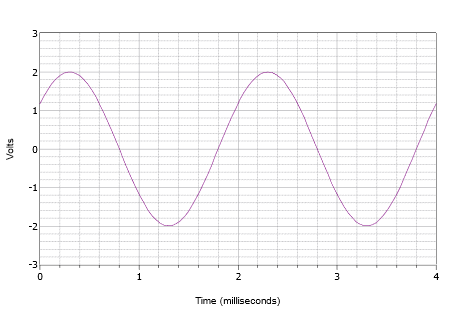
Kuvassa kuvattu aaltomuoto: Aaltomuoto esimerkille \(\PageIndex{2}\).
Ensin positiivinen huippu on 2 volttia ja huipusta huippuun -arvo on 4 volttia. DC-offsetia ei siis ole. Aallon pystysuora keskipiste ei ala \(t = 0\), joten siinä on oltava vaihesiirtymä. Arvo kohdassa \(t = 0\) on 1,2 volttia. Aalto saavuttaa tämän saman amplitudin \(t = 2\) millisekunnissa ja alkaa toistaa toista sykliä. Näin ollen jakson on oltava 2 millisekuntia. Taajuus on tämän arvon käänteisarvo ja siten \(f = 500\) Hz.
Aaltomuoto on siirtynyt vasemmalle, mikä osoittaa positiivista tai etenevää vaiheen siirtymää. Jos tarkastelemme toista sykliä, näemme, että se saavuttaa nollavoltin 1,8 millisekunnin kohdalla. Siirtymä on siis 0,2 millisekuntia. Asteina ilmaistuna tämä on:
\
\
\
Lopullinen lauseke on:
\
Esimerkki \(\PageIndex{3}\)
Piirrä aaltomuoto, joka vastaa seuraavaa lauseketta.
\
Huomaa ensin, että -3 voltin offset painaa positiivisen huipun 5 voltista 2 volttiin ja negatiivisen huipun -5 voltista -8 volttiin. Taajuus 40 kHz sanelee jakson:
\
\
\
\
Vaiheensiirto -72\(^{\circ}\) edustaa 72/360 eli 0,2 jaksoa. Tämä vastaa 0,2 kertaa 25 \(\mu\)s eli 5 \(\mu\)s:n aikaviivettä (oikealle siirrettynä, koska se on negatiivinen).
Aluksi on usein parasta rakentaa kuvaaja sarjan erillisten vaiheiden avulla sen sijaan, että yrittäisi piirtää koko kokonaisuuden yhdellä kertaa. Piirretään ensin siniaalto, jonka huippuamplitudi on 5 volttia ja jakso 25 \(\mu\)s. Paina aaltomuotoa nyt 3 volttia alaspäin niin, että positiivinen huippu on vain 2 volttia ja negatiivinen huippu on -8 volttia. Työnnä lopuksi juuri siirtynyttä aaltomuotoa oikealle 5 \(\mu\)s. Tulos näkyy kuvassa \(\PageIndex{9}\).
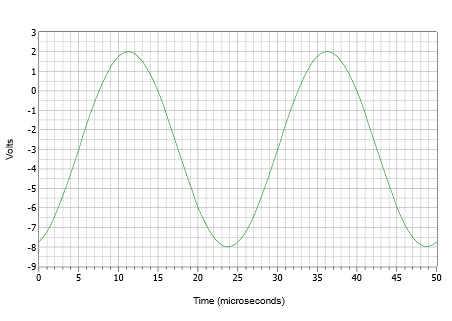
Kuva \(\PageIndex{9}\): Aaltomuoto esimerkissä \(\PageIndex{3}\).
1.2.1: Laboratoriomittaukset
Laboratoriossa käytetään funktiogeneraattoria sinien ja muiden aaltomuotojen tuottamiseen. Nämä laitteet mahdollistavat sekä aallon amplitudin että taajuuden tarkan hallinnan sekä haluttaessa DC-offsetin lisäämisen. Esimerkki on esitetty kuvassa \(\PageIndex{10}\). Vastaava mittausväline on oskilloskooppi tai lyhyesti vain scope.

Kuva \(\PageIndex{10}\): Laboratorion signaaligeneraattori.
Oskilloskooppi on laboratorion ehkä hyödyllisin ja monipuolisin mittauslaite. Tyypillisesti niissä on joko kaksi tai neljä sisääntulokanavaa, vaikka useampikin on mahdollinen. Jokaisella tulokanavalla on oma herkkyyssäätö ja kaikilla kanavilla on yhteinen aikaviite. Näyttö piirtää aaltomuodot samalla tavalla kuin kuvissa \(\PageIndex{1}\) – \(\PageIndex{9}\). Lisäksi ne voivat piirtää yhden jännitteen suhteessa toiseen (X – Y-tila). Nykyaikaisissa oskilloskoopeissa on lisäominaisuuksia, kuten taajuuden, amplitudin, vaiheensiirron jne. automaattinen mittaus, kursoripohjaiset mittaukset ja mahdollisuus tallentaa näyttökuvat grafiikkatiedostoiksi. Esimerkki nelikanavaisesta digitaalisesta oskilloskoopista on esitetty kuvassa \(\PageIndex{11}\).

Kuva \(\PageIndex{11}\): Digitaalinen oskilloskooppi.
1.2.2: Kaaviosymbolit
Kuvassa \(\PageIndex{12}\) on esitetty vaihtojännite- ja virtalähteiden symbolit. Napaisuus- ja suuntamerkinnät eivät ole ehdottomia; onhan kyse vaihtovirtalähteistä, joiden napaisuus ja suunnat vaihtuvat edestakaisin. Sen sijaan merkintöjä käytetään ajoitusviitteen luomiseen, erityisesti piireissä, joissa käytetään useita lähteitä.
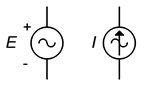
Kuva \(\PageIndex{12}\): Vaihtojännitelähteen (vasemmalla) ja virtalähteen (oikealla) kaavamaiset symbolit.
On syytä muistaa, että lähteen nollaaminen on sama kuin sen napaisuuden kääntäminen. Tämä päti tasavirtalähteisiin ja pätee edelleen vaihtovirtalähteisiin. Tätä havainnollistetaan kuvassa \(\PageIndex{13}\). Joskus lähteen kääntäminen tai nollaaminen tekee analyysistä hieman ilmeisemmän tai helpommin havainnollistettavan.
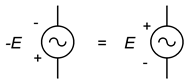
Kuva \(\PageIndex{13}\): Napaisuuden/merkkien vastaavuus.
Esimerkki \(\PageIndex{4}\)
Asetetaan, että oskilloskooppi näyttää kaksi aaltoa kuvan \(\PageIndex{14}\) mukaisesti. Määritä pienemmän 20 voltin huipun (sininen) aaltomuodon vaihesiirtymä suhteessa suurempaan 25 voltin huipun (punainen) aaltomuotoon.
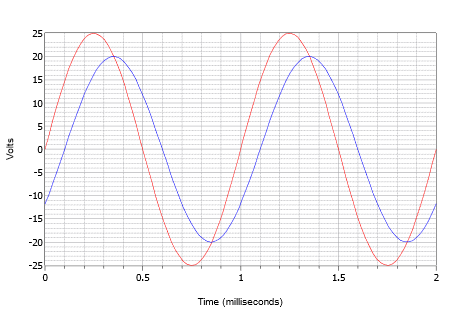
Kuva \(\PageIndex{14}\): Esimerkin \(\PageIndex{4}\) aaltomuodot.
Huomaa ensinnäkin, että kummassakaan aallossa ei ole DC-offsetia. Jos jommallakummalla tai molemmilla olisi offset, aaltoa (aaltoja) olisi siirrettävä pystysuunnassa, jotta niiden normaalit nollakohdat olisivat samalla tasolla. Mitattaessa kumpaakin aaltoa jakson havaitaan olevan 1 millisekunti. Aikasiirtymä löytyy helpoimmin mistä tahansa nollakohdasta (valittavana on neljä kohtaa). Viive on yksi pieni poikkeama eli 0,1 millisekuntia, jolloin pienempi aalto on ajallisesti viivästynyt eli jäljessä suuremmasta aallosta. Tämä osoittaa negatiivista vaihesiirtymää.
\
\
\
\
1.2.3. Vaiheensiirtymä: Sinit ja kosinukset
On olemassa kourallinen erityisiä vaihesiirtymiä, jotka ovat tarkemman tarkastelun arvoisia. Jos siniaalto käännetään eli käännetään ylösalaisin, sitä ei voi erottaa siniaallosta, jota on siirretty joko +180 tai -180 astetta. Toisin sanoen tällainen aalto voidaan kirjoittaa kolmella eri tavalla: \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\) tai \(\sin (2 \pi ft + 180^{\circ})\). Jos siniaaltoa siirretään +90 astetta (eli eteenpäin ja vasemmalle), sitä voidaan kutsua myös kosiniaalloksi. Näin ollen \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Lopuksi, jos siniaaltoa siirretään -90 astetta (eli se on jäljessä ja oikealla), sitä voidaan kutsua negatiiviseksi tai käänteiseksi kosiniaalloksi. Näin ollen \(\sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). Näiden neljän aallon suhteet on esitetty kuvassa \(\PageIndex{15}\).
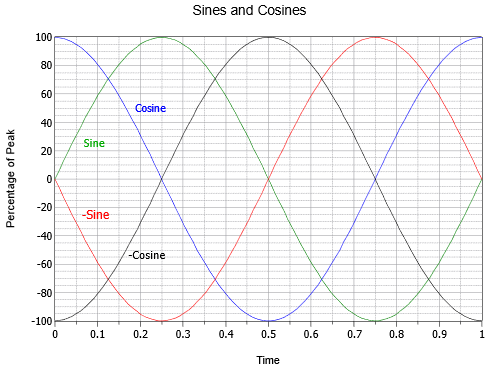
Kuva \(\PageIndex{15}\): Sinien ja kosinusten väliset aikasuhteet.
On myös syytä huomata, että kosiniaalto edustaa siniaallon ensimmäistä derivaattaa eli kaltevuutta. Kuten ehkä muistat muista tutkimuksista, viivan kaltevuus tai ”jyrkkyys” on pystysuuntaisen muutoksen suhde vaakasuuntaiseen muutokseen, jota joskus kutsutaan ”nousuksi juoksuun nähden”. Jännitteen osalta se on jännitteen muutos suhteessa ajan muutokseen eli \(\Delta V/ \Delta t\). Tasaisen, jatkuvasti muuttuvan käyrän, kuten siniaallon, kaltevuus tietyssä pisteessä määritellään asianmukaisesti ensimmäisenä derivaatana eli tässä tapauksessa \(dv/dt\). Voit varmistaa, että tämä pitää paikkansa visuaalisesti, kun huomaat, että siniaallon jyrkin kohta (vihreä) on kohdassa, jossa se ylittää nolla-amplitudin. Kun se ylittää nollapisteen liikkuessaan positiivisesti (\(t = 0\) tai \(t = 1\) kuvassa \(\PageIndex{15}\)), kosini (sininen) on positiivisessa huipussaan. Kun sini ylittää nollan liikkuessaan negatiivisesti (kohdassa \(t = 0,5\)), kosinus on negatiivisessa huipussaan. Lisäksi siniaalto on tasainen ja sen kaltevuus on nolla sen positiivisen ja negatiivisen huipun kohdalla (\(t = 0,25\) ja \(t = 0,75\)), ja näinä aikoina myös kosinuksen amplitudi on nolla. On myös totta, että siniaalto on negatiivisen kosiniaallon kaltevuus, negatiivinen kosini on negatiivisen sinin kaltevuus ja negatiivinen sini on kosinin kaltevuus. Käänteissuunnassa voidaan sanoa, että kosiniaallon antiderivaatta (epämääräinen integraali) on siniaalto, siniaallon integraali on negatiivinen kosiniaalto ja niin edelleen. Nämä suhteet osoittautuvat hyödyllisimmiksi, kun kiinnitämme huomiota kondensaattoreiden ja induktoreiden vasteeseen vaihtovirtapiireissä.
1.2.4: RMS – Root Mean Square Measurement
Huipun ja huipusta huippuun -arvon ohella amplitudi voidaan ilmoittaa RMS-arvona (Root Mean Square). Itse asiassa, jos huippua tai huipusta huippuun -arvoa ei ole määritetty, mittauksen oletetaan olevan RMS. RMS on erityinen laskutapa, jota käytetään ekvivalentin tasavirtatehon määrittämiseen (hyvin yleistä esimerkiksi äänitehovahvistimissa). Toisin sanoen, jos olemme kiinnostuneita löytämään vastuksen tehon, laskenta on suoritettava käyttäen jännitteen tai virran RMS-arvoja, ei huippuarvoja tai huipusta-huippuun -arvoja. Jos näin ei tehdä, saadaan virheellisiä tehoja. Tämä pätee riippumatta aallonmuodosta, olipa kyseessä sitten siniaalto, kolmioaalto tai musiikkisignaalien monimutkaiset aallot. Jos jännite määritetään RMS-arvona, sitä voidaan käsitellä teholaskennassa aivan kuten vastaavan kokoista tasajännitettä. Esimerkiksi 1 voltin RMS-sinijännite tuottaa saman tehohäviön ja kuumenemisen tietyssä vastuksessa kuin 1 voltin tasavirtajännite. Tästä syystä RMS:ään viitataan joskus tehollisarvona (eli tehollisena DC-arvona).
Nimi root-mean-square kuvaa tehollisen arvon määritysprosessia. Muistetaan ensin, että teho on verrannollinen jännitteen tai virran neliöön. Näin ollen ensimmäinen askeleemme on tuloaaltomuodon neliöiminen. Aaltomuoto on tietysti ajan funktio, ja sen neliö antaa jonkin uuden muodon. Tässä vaiheessa meidän on löydettävä tämän uuden muodon keskiarvo. Syy tähän on yksinkertainen, mutta ei välttämättä itsestään selvä. Sähkö- ja elektroniikkakomponenteilla on massaa, eivätkä ne siten lämpene tai jäähty hetkessä. Niillä on terminen aikavakio. Siksi ne reagoivat keskimääräiseen syötteeseen ajan kuluessa. Vaikka voisimme laskea jonkinlaisen ”hetkellisen huipputehon” jollakin tietyllä ajanhetkellä, se ei edusta vastaavaa tasavirtatehoa. Kun olemme saaneet tämän neliöllisen aaltomuodon keskiarvon, vastaava DC-arvo on vain keskiarvon neliöjuuri. Tuloksena on nollan ja yhden välinen murtoluku, jota käytetään skaalauskertoimena huippuarvon muuttamiseksi RMS-arvoksi. Arvo on yksilöllinen tietylle aaltomuodolle. Toisin sanoen kaikilla sinimuotoisilla aalloilla (vaiheesta riippumatta) on sama kerroin, kaikilla säännöllisillä kolmioaalloilla on sama kerroin ja niin edelleen. Koska käsittelemme enimmäkseen sinimuotoisia aaltoja, tarkastellaan tarkemmin niiden RMS-kertoimen määrittämistä.
Aloitetaan siniaallon peruslausekkeella, jossa ei ole DC-offsetia tai vaihesiirtoa ja jonka amplitudi on yksi:
\
Ensimmäinen vaihe on tämän aaltomuodon neliöiminen. Hyödyllinen trigonometrinen identiteetti on
\
Soveltamalla tätä aaltoomme saadaan:
\
Tämä lauseke kuvaa käänteistä kosiniaaltoa, jonka taajuus on kaksinkertainen alkuperäiseen taajuuteen nähden ja jonka amplitudi on puolet alkuperäisestä, ja joka ratsastaa DC-offsetilla, joka on yhtä suuri kuin sen huippuarvo. Toisin sanoen kosinuksen negatiivinen huippu on nollassa ja positiivinen huippu on 1. Seuraava askel on löytää tämän välituloksen keskiarvo tai keskiarvo. Keskiarvo on yhtä suuri kuin offset 0,5. Tämä voidaan havainnollistaa siten, että offsetin yläpuolella oleva alue täyttää täydellisesti offsetin alapuolella olevan ”notkelman”. Viimeisenä vaiheena otetaan keskiarvon neliöjuuri. Neliöjuuri 0,5:stä on yhtä suuri kuin yksi yli kahden neliöjuuren eli noin 0,707. Näin ollen RMS-arvo on 0,707 kertaa huippuarvo. Vaihtoehtoisesti voit jakaa huipun neliöjuurella kahdesta eli noin 1,414. Tämä prosessi on esitetty graafisesti kuvassa \(\PageIndex{16}\).
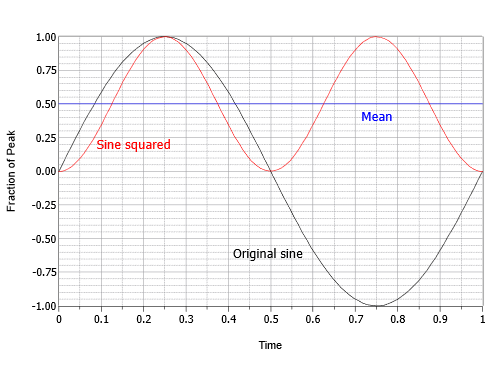
Kuva \(\PageIndex{16}\): Process to find RMS factor for sines.
Summatiivisesti siniaaltojen RMS on aina huippuarvo kertaa 0,707. Voidaan myös sanoa, että minkä tahansa siniaallon RMS-arvo on sen huippuarvo jaettuna noin 1,414:llä. Nämä suhdeluvut eivät taas välttämättä päde ei-siniaalloille. Muita yleisiä muotoja koskevat tiedot löytyvät lisäyksestä C. Huippuarvon ja RMS-arvon suhdetta kutsutaan huippusuhteeksi. Tämä on kiinteä arvo siniaalloille (jälleen noin 1,414), mutta voi olla yli 10:1 joillakin äänisignaalityypeillä.
1.2.5: Aallonpituus
Toinen kiinnostava asia on aallon etenemisnopeus. Tämä vaihtelee suuresti. Valon tapauksessa tyhjiössä (tai lähempänä sähkövirran tapauksessa johdossa) nopeus on noin 3E8 metriä sekunnissa (eli 300 000 km/s) tai noin 186 000 mailia sekunnissa.
Antaen nopeuden ja jakson voimme kuvitella, kuinka kaukana toisistaan aallon huiput ovat. Tätä etäisyyttä kutsutaan aallonpituudeksi ja sitä merkitään kreikkalaisella kirjaimella lambda \(\lambda\). Aallonpituus on yhtä suuri kuin nopeus jaettuna taajuudella \(\lambda = v/f\). Näin ollen 100 Hz:n siniä tuottavan kaiuttimen äänen nopeus ilmassa on 344 m/s, jolloin \(\lambda = 344 m/s \, / \, 100\) Hz eli 3,44 metriä (hieman yli 11 jalkaa). Huomaa, että mitä suurempi taajuus, sitä lyhyempi aallonpituus. Huomaa myös, että mitä nopeampi nopeus, sitä pidempi aallonpituus. Aallonpituuslaskelmat ovat erityisen tärkeitä televiestinnän ja akustiikan aloilla.