Sisällysluettelo
Koordinaattimuunnokset eivät ole tarpeeksi intuitiivisia 2D:ssä, ja ne ovat suorastaan tuskallisia 3D:ssä. Tällä sivulla käsitellään niitä seuraavassa järjestyksessä: (i) vektorit 2D:ssä, (ii) tensorit 2D:ssä, (iii) vektorit 3D:ssä, (iv) tensorit 3D:ssä ja lopuksi(v) 4. asteen tensorimuunnokset.
Koordinaattitransformaatioiden tärkeä näkökohta on transformaatiomatriisin arviointi, erityisesti kolmiulotteisissa muunnoksissa. Tätä käsitellään tässä, ja sitä käsitellään perusteellisesti seuraavalla sivulla.
On erittäin tärkeää ymmärtää, että kaikki tällä sivulla esitetyt koordinaattimuunnokset ovat koordinaatiston kiertoja, kun taas itse kohde pysyy paikallaan. ”Kohde” voi olla vektori, kuten voima tai nopeus, tai tensori, kuten jännitys tai venymä komponentissa. Kohteiden kiertoja käsitellään myöhemmissä kappaleissa.
Vektoreiden 2D-koordinaattimuunnokset
Akatemiallinen peruna antaa erinomaisen esimerkin siitä, miten koordinaattimuunnoksia sovelletaan vektoreihin, ja samalla korostetaan, että koordinaatisto pyörii eikä vektori… tai peruna.
Vasemmalla olevalla perunalla on vektori. Joten perunaan on lisätty koordinaatisto, kuten oikealla on esitetty, jolloin vektori voidaan nyt kuvata muodossa \({\bf v} = 2{\bf i} + 9{\bf j}\).

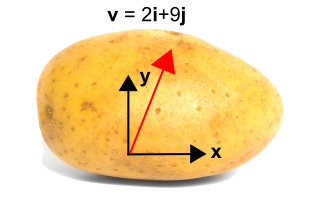
Nyt otamme käyttöön alla sinisellä esitetyn pyöritetyn koordinaatiston käyttäen\(x’\) ja \(y’\). Uutta järjestelmää käännetään vastapäivään kulmalla \(\theta\) alkuperäisestä koordinaatistosta. Huomaa, että itse vektori ei muutu lainkaan. Se on edelleen sama vektori kuin ennenkin. Sitä kuvataan kuitenkin eri lukuarvoilla uudessa koordinaatistossa. Tässä tapauksessa vektori on lähempänä uuden \(x’\)-akselin kuin \(y’\)-akselin suuntainen, joten \(\bf i’\)-komponentti on suurempi kuin \(\bf j’\)-komponentti. Muunnos on esitetty kuvan alla.
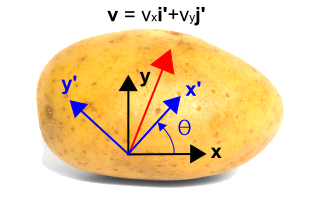
\\\
Tämä nähdään toteamalla, ettäNämä neljä tekijää muodostavat muunnosyhtälöiden neljä termiä. Ne on helppo tarkistaa asettamalla \(\theta = 0^\circ \) ja \(\theta = 90^\circ \). Kun \(\theta = 0^\circ\), niin \(v’_x = v_x\) ja \(v’_y = v_y\). Kun \(\theta = 90^\circ\), niin \(v’_x = v_y\) ja \(v’_y = -v_x\).
Muunnosmatriisi
On kätevämpää kirjoittaa (ja työskennellä) muunnosyhtälöt matriisien avulla.
\\\left\{ \matrix {v_x \\\ v_y} \right\\}}\]
Termit \(\cos \theta\) ovat matriisin diagonaalilla, kun taas termit \(\sin \theta\) ovat diagonaalin ulkopuolella. Ainoa mahdollinen ongelma on muistaa, missä \(\sin \theta\)-termissä on miinusmerkki. Se on aina vasemmassa alakulmassa oleva termi.
Yllä oleva yhtälö kirjoitetaan matriisimerkinnöin
\
, jossa \({\bf Q}\) on tavallinen kirjain, joka on valittu muunnosmatriisille.

Transformaatio- vs. rotaatiomatriisit
Jos tämä aihe ei olisi jo tarpeeksi vaikea, monet kirjat ja verkkosivut lisäävät sekaannusta jättämällä selventämättä, mikä on kiinteää ja mikä rotaatiota. Tällä ja seuraavalla sivulla koordinaatisto pyörii kohteen pysyessä kiinteänä, joten tässä käytetään termiä transformaatiomatriisi tämän korostamiseksi.
Käsittelemme kuitenkin myöhemmin tilanteita, joissa kohde pyörii koordinaatiston pysyessä kiinteänä. Tässä skenaariossa käytetään termiä rotaatiomatriisi korostamaan sitä, että kohde pyörii.
Paljon sekaannusta syntyy siitä hämmästyttävästä seikasta, että jokainen matriisi (transformaatio ja rotaatio) on vain toistensa transpoosi! Ne näyttävät siis äärimmäisen samankaltaisilta. Kaksiulotteisissa ongelmissa ainoa käytännöllinen ero on se, onko \(\sin \theta\)-termin edessä oleva miinusmerkki \(q_{12}\)-termissä vai \(q_{21}\)-termissä.
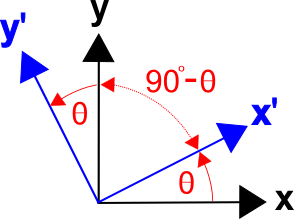
Transformaatiomatriisien muotoilemiseksi on olemassa yleinen menetelmä, joka perustuu molempien koordinaatistojen akselien välisten kulmien kosinuksiin eli suuntakosinuksiin. (Tämä pätee myös kolmiulotteisiin muunnoksiin.) Muunnosmatriisi voidaan kirjoittaa muodossa
\\\]
, jossa \((x’,x)\) edustaa \(x’\) ja \(x\)-akselien välistä kulmaa,\((x’,y)\) on \(x’\) ja \(y\)-akselien välinen kulma jne.
\(x’\) ja \(y\) välinen kulma on \((90^\circ – \theta)\) ja \(\cos(x’,y) = \cos(90^\circ – \theta) = \sin \theta\).
Vastaavasti \(y’\) ja \(x\) välinen kulma on \((90^\circ + \theta)\), ja \(\cos(y’,x) = \cos(90^\circ + \theta) = -\sin \theta\).
Tensorimerkintä
Koordinaattimuunnos kirjoitetaan tensorimerkinnällä
\
, jossa \(\lambda_{ij}\) on muunnosmatriisi \({\bf Q}\). (En tiedä, miksi\({\bf Q}\) käytetään matriisimuodossa, mutta tensorimuodossa käytetään \(\lambda_{ij}\), ei \(q_{ij}\)).) \(\lambda_{ij}\) määritellään seuraavasti:
\
Jos esimerkiksi \(i = 1\) ja \(j = 2\), niin
\
\(\lambda_{ij}\) on \(x’_i\)-akselin ja \(x_j\)-akselin välisen kulman suunnan kosini. Tämäkin pätee yhtä lailla myös kolmiulotteisiin muunnoksiin.
Tensoreiden 2D-koordinaattimuunnokset
Tässä kappaleessa esitellään tensorimuunnosten mitä ja miten.miksi saa odottaa myöhempään.
Koordinaattimuunnokset 2. asteen tensoreille sisältävät aivan saman \({\bf Q}\)matriisin kuin vektorimuunnokset. Jännitystensorin \(\boldsymbol{\sigma}\) muunnos referenssikoordinaatistosta \(x-y\) koordinaatistoon \(\boldsymbol{\sigma’}\) uudessa \(x’-y’\)-järjestelmässä tehdään seuraavasti.
\
Kirjoittamalla matriisit eksplisiittisesti saadaan
\ = \vasen \vasen \vasen \vasen \vasen \]
(Huomaa, että jännitystensori on aina symmetrinen, myös muunnosten jälkeen.)
Matriisien kertominen keskenään antaa
\
Nämä kolme yhtälöä ovat täsmälleen jännitystensorin 2-D-muunnos, joka saadaan, kun lasketaan yhteen differentiaalielementtiin kohdistuvat voimat ja asetetaan tasapaino. Tätä edustaa myös Mohrin ympyrä.
Tensorimerkintätapa
Koordinaattimuunnos kirjoitetaan tensorimerkinnällä
\
Kuten tavallista, tensorimerkintätapa antaa lisäymmärrystä prosessiin. Tällä kertaa oivallus tulee lambdojen alaindekseistä. Jokainen lambda yhdistää tehokkaasti \(\boldsymbol{\sigma’}\):n alaviitteen \(\boldsymbol{\sigma}\):n alaviitteen \(\boldsymbol{\sigma}\):n alaviitteeseen.Tämä pätee tensorin arvosta riippumatta.
Vektoreiden kolmiulotteiset koordinaattimuunnokset
Monet 2D-muunnoksissa käytetyt yleiset yhtälöt ovat sovellettavissa myös kolmiulotteisesti.Esimerkkeinä mainittakoon
\\
Vain nyt yksityiskohdat ovat erilaisia. Vektoreilla on z-komponentit ja muunnosmatriisit ovat 3×3 eikä 2×2.
\\\]
\\]
\\ \left\{ \matrix { v_x \\\\ v_y \\\\ v_z } \right\}\\]
Tensoreiden kolmiulotteiset koordinaattimuunnokset
Jälleen kerran säännöt eivät muutu, vain yksityiskohdat muuttuvat.
\
Kirjoittamalla matriisit eksplisiittisesti ulos saadaan
\\ = \left\left\left\left\\\]
Tämä verkkosivu suorittaa kolmiulotteisten tensoreiden koordinaattimuunnokset. Kokeile sitä.
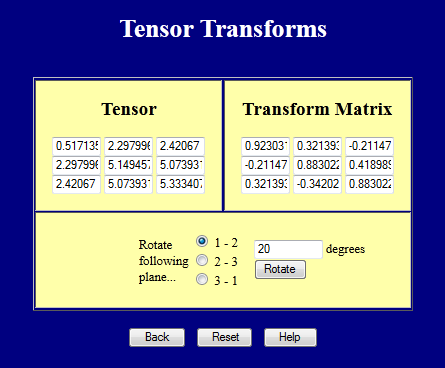
Koordinaattimuunnokset 4. sijan tensoreille
Hooken lakia käsittelevässä kappaleessa näemme, että jäykkyystensori on4. sijan tensori, eli 3x3x3x3 (ei 4×4). Se kirjoitetaan muotoon \(C_{ijkl}\), koska se suhteuttaa minkä tahansa muodonmuutoskomponentin, \(\epsilon_{kl}\), mihin tahansa jännityskomponenttiin, \(\sigma_{ij}\), ts, \(\sigma_{ij} = C_{ijkl} \epsilon_{kl}\).Koordinaattitransformaatiolaki neljännen asteen jäykkyystensorille on helppo kirjoittaa tensorimuodossa seuraavasti:
\
Tensoriyhtälö ohjaa, miten transformaatio kirjoitetaan matriisimuodossa.
\
Yhteenveto
Vektorin koordinaattitransformaatio matriisi- ja tensorimuodossa on
\
Tensorin koordinaattitransformaatio matriisi- ja tensorimuodossa on
\
Huomaa, että \({\bf Q}\) ja \(\lambda_{ij}\) ovat sama muunnosmatriisi.
Kaksiulotteisessa muodossa \({\bf Q}\) ja \(\lambda_{ij}\) määritellään seuraavasti
\\\]
, mikä on erikoistapaus yleisemmästä kolmiulotteisesta muodosta
\\\]
.