Katso ennen jatkoa kaikki tässä artikkelissa käsitellyt aiheet:
- Mikä on SciPy?
- NumPy vs SciPy
- SciPyn alipaketit
- Perusfunktiot
- Erikoisfunktiot
- Integrointifunktiot
- Optimointifunktiot
- Fourier-muunnosfunktiot
- Signaali Processing Functions
- Lineaarialgebra
- Sparse Eigenvalues
- Spatial Data Structures and Algorithms
- Multidimensional Image Processing Functions
- File IO
Aloitetaan siis. 🙂
SciPy on avoimen lähdekoodin Python-kirjasto, jota käytetään tieteellisten ja matemaattisten ongelmien ratkaisemiseen. Se on rakennettu NumPy-laajennuksen varaan, ja sen avulla käyttäjä voi käsitellä ja visualisoida dataa monenlaisilla korkean tason komennoilla. Kuten aiemmin mainittiin, SciPy rakentuu NumPy:n varaan, joten jos tuodaan SciPy:tä, ei tarvitse tuoda NumPy:tä.
NumPy vs SciPy
Kumpikin NumPy ja SciPy ovat Python-kirjastoja, joita käytetään matemaattiseen ja numeeriseen analyysiin. NumPy sisältää matriisitiedot ja perusoperaatiot, kuten lajittelu, indeksointi jne. kun taas SciPy koostuu kaikesta numeerisesta koodista. Vaikka NumPy tarjoaa useita funktioita, joiden avulla voidaan ratkaista lineaarialgebra, Fourier-muunnokset jne., SciPy on kirjasto, joka itse asiassa sisältää näiden funktioiden ja monien muiden funktioiden täysin varustetut versiot. Jos kuitenkin teet tieteellistä analyysiä Pythonilla, sinun on asennettava sekä NumPy että SciPy, koska SciPy perustuu NumPyyn.
SciPyn alipaketit:
SciPyssä on useita alipaketteja erilaisia tieteellisiä laskutoimituksia varten, jotka on esitetty seuraavassa taulukossa:

Edellisen yksityiskohtaisen selostuksen saat kuitenkin virallisesta dokumentoinnista.
Nämä paketit on tuotava yksinomaan ennen niiden käyttöä. Esimerkiksi:
from scipy import cluster
Ennen kuin tarkastellaan kutakin näistä funktioista yksityiskohtaisesti, tarkastellaan ensin funktioita, jotka ovat yhteisiä sekä NumPy:ssä että SciPy:ssä.
Vuorovaikutus NumPy:n kanssa:
SciPy rakentuu NumPy:n varaan, ja siksi voit käyttää NumPy:n funktioita itsessään hyväksi käsitellessäsi määriä. Jos haluat tietää syvällisemmin näistä funktioista, voit yksinkertaisesti käyttää help()-, info()- tai source()-funktioita.
help():
Voidaksesi saada tietoa mistä tahansa funktiosta, voit käyttää help()-funktiota. Tätä funktiota voidaan käyttää kahdella tavalla:
- ilman parametreja
- käyttäen parametreja
Tässä on esimerkki, joka näyttää molemmat edellä mainitut tavat:
from scipy import cluster
help(cluster) #with parameter
help() #without parameter
Kun suoritat yllä olevan koodin, ensimmäinen help()-funktio palauttaa tiedot klusterin alamoduulista. Toinen help() pyytää käyttäjää syöttämään minkä tahansa moduulin, avainsanan jne. nimen, josta käyttäjä haluaa etsiä tietoa. Lopettaaksesi tämän funktion suorittamisen kirjoita yksinkertaisesti ’quit’ ja paina enteriä.
info():
Tämä funktio palauttaa tietoa halutuista funktioista, moduuleista jne.
scipy.info(cluster)
source():
Lähdekoodi palautetaan vain Python-kielellä kirjoitetuista objekteista. Tämä funktio ei palauta hyödyllistä tietoa, jos metodit tai objektit on kirjoitettu jollain muulla kielellä, kuten C:llä. Jos kuitenkin haluat hyödyntää tätä funktiota, voit tehdä sen seuraavasti:
scipy.source(cluster)
Erikoisfunktiot:
SciPy tarjoaa joukon erikoisfunktioita, joita käytetään matemaattisessa fysiikassa, kuten elliptiset funktiot, mukavuusfunktiot, gamma- ja beetafunktiot, jne. Kaikkien funktioiden etsimiseen voit käyttää aiemmin kuvattua help()-funktiota.
Eksponentti- ja trigonometriset funktiot:
SciPyn erikoisfunktiopaketti tarjoaa useita funktioita, joiden avulla voit löytää eksponentteja ja ratkaista trigonometrisiä ongelmia.
Tarkastellaan seuraavaa esimerkkiä:
Esimerkki:
from scipy import special
a = special.exp10(3)
print(a)
b = special.exp2(3)
print(b)
c = special.sindg(90)
print(c)
d = special.cosdg(45)
print(d)
TULOS:
1000.0
8.0
1.0
0.7071067811865475
SciPyn erikoisfunktiopaketissa on monia muitakin funktioita, joita voit kokeilla itse.
Integraalifunktiot:
SciPy tarjoaa useita funktioita integraalien ratkaisemiseen. Tavallisesta differentiaaliintegraattorista aina trapetsisääntöjen käyttämiseen integraalien laskemiseen, SciPy on funktioiden varasto kaikenlaisten integraaliongelmien ratkaisemiseen.
Yleinen integraatio:
SciPy tarjoaa quad-nimisen funktion, jolla voidaan laskea integraali funktiosta, jolla on yksi muuttuja. Rajat voivat olla ( ) osoittamaan äärettömiä rajoja. Quad()-funktion syntaksi on seuraava:
SYNTAX:
quad(func, a, b, args=(), full_output=0, epsabs=1.49e-08, epsrel=1.49e-08, limit=50, points=None, weight=None, wvar=None, wopts=None, maxp1=50, limlst=50)
Tässä funktio integroidaan rajojen a ja b välissä (voi olla myös ääretön).
ESIMERKKI:
from scipy import special
from scipy import integrate
a= lambda x:special.exp10(x)
b = scipy.integrate.quad(a, 0, 1)
print(b)
Yllä olevassa esimerkissä funktio ’a’ evaluoidaan rajojen 0, 1 välillä. Kun tämä koodi suoritetaan, näet seuraavan tulosteen.
TULOS:
(3.9086503371292665, 4.3394735994897923e-14)
Kaksoisintegraalifunktio:
SciPy:ssä on dblquad, jota voidaan käyttää kaksoisintegraalien laskemiseen. Kaksoisintegraali, kuten monet meistä tietävät, koostuu kahdesta reaalisesta muuttujasta. Funktio dblquad() ottaa parametrikseen integroitavan funktion sekä neljä muuta muuttujaa, jotka määrittelevät raja-arvot ja funktiot dy ja dx.
ESIMERKKI:
from scipy import integrate
a = lambda y, x: x*y**2
b = lambda x: 1
c = lambda x: -1
integrate.dblquad(a, 0, 2, b, c)
TULOS:
-1.33333333333333333335, 1.480297366166868755e-14)
SciPy tarjoaa useita muita funktioita kolmoisintegraalien, n-integraalien, Rombergin integraalien jne. arviointiin, joihin voit tutustua tarkemmin. Löydät kaikki yksityiskohdat tarvittavista funktioista käyttämällä help-funktiota.
Optimointifunktiot:
Scipy.optimize tarjoaa useita yleisesti käytettyjä optimointialgoritmeja, joihin voit tutustua help-funktion avulla.
Se koostuu periaatteessa seuraavista:
- Monimuuttujaisten skalaarifunktioiden rajoittamaton ja rajoitettu minimointi eli minimointi (esim. BFGS, Newton Conjugate Gradient, Nelder_mead simplex, jne.)
- Globaalit optimointirutiinit (esim. differential_evolution, dual_annealing, jne)
- Vähimmän neliöiden minimointi ja käyrän sovitus (esim. least_squares, curve_fit, jne)
- Skalaaristen yksimuuttujaisten funktioiden minimointilaitteet ja juurenetsijät (esim. minimize_scalar ja root_scalar)
- Multimuuttujayhtälösysteemien ratkaisijat, jotka käyttävät algoritmeja, kuten hybridi-Powell, Levenberg-Marquardt.
Rosenbrook-funktio:
Rosenbrook-funktio ( rosen) on testiongelma, jota käytetään gradienttipohjaisille optimointialgoritmeille. Se on määritelty SciPy:ssä seuraavasti:

ESIMERKKI:
import numpy as np
from scipy.optimize import rosen
a = 1.2 * np.arange(5)
rosen(a)
TULOS: 7371.039999999999945
Nelder-Mead:
Nelder-Mead-menetelmä on numeerinen menetelmä, jota käytetään usein funktion min/maksimin määrittämiseen moniulotteisessa avaruudessa. Seuraavassa esimerkissä käytetään minimointimenetelmää yhdessä Nelder-Mead-algoritmin kanssa.
ESIMERKKI:
from scipy import optimize
a =
b = optimize.minimize(optimize.rosen, a, method='Nelder-Mead')
b.x
OUTPUT: array()
Interpolointifunktiot:
Numeerisen analyysin alalla interpoloinnilla tarkoitetaan uusien datapisteiden rakentamista tunnettujen datapisteiden joukon sisällä. SciPy-kirjastossa on scipy.interpolate-niminen alipaketti, joka koostuu spline-funktioista ja -luokista, yksi- ja moniulotteisista (yksi- ja monimuuttujainen) interpolointiluokista jne.
Yksiulotteinen interpolointi:
Yksiulotteinen interpolointi on pohjimmiltaan käyränsovituksen osa-alue, jossa etsitään käyrä, joka antaa tarkan sovituksen kaksiulotteisten datapisteiden sarjalle. SciPy tarjoaa interp1d-funktion, jota voidaan hyödyntää yksimuuttujaisen interpoloinnin tuottamiseen.
EXAMPLE:
import matplotlib.pyplot as plt
from scipy import interpolate
x = np.arange(5, 20)
y = np.exp(x/3.0)
f = interpolate.interp1d(x, y)x1 = np.arange(6, 12)
y1 = f(x1) # use interpolation function returned by `interp1d`
plt.plot(x, y, 'o', x1, y1, '--')
plt.show()
OUTPUT:
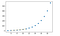
Multimuuttujainen interpolointi:
Multimuuttujainen interpolointi (spatiaalinen interpolointi ) on eräänlainen interpolointi funktioille, jotka koostuvat useammasta kuin yhdestä muuttujasta. Seuraava esimerkki havainnollistaa esimerkin
Interpolointi 2-D ruudukon yli käyttämällä funktiota interp2d(x, y, z) periaatteessa käyttää x, y, z -matriiseja approksimoimaan jotakin funktiota interp2d-funktio. f: ”z = f(x, y)” ja palauttaa funktion, jonka kutsumenetelmä käyttää spline-interpolointia löytääkseen uusien pisteiden arvon.
ESIMERKKI:
from scipy import interpolate
import matplotlib.pyplot as plt
x = np.arange(0,10)
y = np.arange(10,25)
x1, y1 = np.meshgrid(x, y)
z = np.tan(xx+yy)
f = interpolate.interp2d(x, y, z, kind='cubic')
x2 = np.arange(2,8)
y2 = np.arange(15,20)
z2 = f(xnew, ynew)
plt.plot(x, z, 'ro-', x2, z2, '--')
plt.show()
TULOS:

Fourier-muunnosfunktiot:
Fourier-analyysi on menetelmä, joka käsittelee funktion ilmaisemista jaksollisten komponenttien summana ja signaalin talteenottoa näistä komponenteista. Fft-funktioiden avulla voidaan palauttaa reaalisen tai kompleksisen sarjan diskreetti Fourier-muunnos.
ESIMERKKI:
from scipy.fftpack import fft, ifft
x = np.array()
y = fft(x)
print(y)
TULOS:
Vastaavasti tämän käänteisluku voidaan löytää käyttämällä ifft-funktiota seuraavasti:
EXAMPLE:
rom scipy.fftpack import fft, ifft
x = np.array()
y = ifft(x)
print(y)
OUTPUT:
Signaalinkäsittelyfunktiot:
Signaalinkäsittelyssä käsitellään signaalien, kuten äänen, kuvan jne. analysointia, muokkaamista ja syntetisointia. SciPy tarjoaa joitakin funktioita, joiden avulla voit suunnitella, suodattaa ja interpoloida yksi- ja kaksiulotteista dataa.
Suodatus:
Suodattamalla signaalia periaatteessa poistat siitä ei-toivotut komponentit. Voit suorittaa järjestetyn suodatuksen käyttämällä order_filter-funktiota. Tämä funktio suorittaa periaatteessa järjestetyn suodatuksen joukolle. Tämän funktion syntaksi on seuraava:
SYNTAX:
order_filter(a, domain, rank)
a = N-ulotteinen syötematriisi
domain = maskimatriisi, jolla on sama määrä ulottuvuuksia kuin `a`
rank = Ei-negatiivinen luku, joka valitsee elementit listasta sen jälkeen, kun se on lajiteltu (0 on pienin, jota seuraa 1…)
Esimerkki:signal-alipaketti koostuu myös erilaisista funktioista, joita voidaan käyttää aaltomuotojen tuottamiseen. Yksi tällainen funktio on chirp. Tämä funktio on taajuussuuntainen kosinogeneraattori ja sen syntaksi on seuraava:
SYNTAX:
chirp(t, f0, t1, f1, method=’linear’, phi=0, vertex_zero=True)
where,

from scipy.signal import chirp, spectrogram
import matplotlib.pyplot as plt
t = np.linspace(6, 10, 500)
w = chirp(t, f0=4, f1=2, t1=5, method='linear')
plt.plot(t, w)
plt.title("Linear Chirp")
plt.xlabel('time in sec)')
plt.show()
ULOSTULO:

Lineaarialgebra:
Lineaarialgebra käsittelee lineaarisia yhtälöitä ja niiden esittämistä vektoriavaruuksien ja matriisien avulla. SciPy perustuu ATLAS LAPACK- ja BLAS-kirjastoihin ja on erittäin nopea lineaarialgebraan liittyvien ongelmien ratkaisemisessa. Kaikkien numpy.linalg:n funktioiden lisäksi scipy.linalg tarjoaa myös useita muita kehittyneitä funktioita. Myös jos numpy.linalgia ei käytetä yhdessä ATLAS LAPACK- ja BLAS-tuen kanssa, scipy.linalg on nopeampi kuin numpy.linalg.
Matriisin käänteisluvun löytäminen:
Matemaattisesti matriisin A käänteisluku (inverse) on matriisi, joka on sellainen, että missä on identtisyysmatriisi, joka koostuu ykkösistä päädiagonaalilla, jota merkitään B=A-1. SciPy:ssä tämä käänteisluku saadaan käyttämällä metodia linalg.inv.
EXAMPLE:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.inv(A)
print(B)
OUTPUT:
]
Determinanttien löytäminen:
Matriisin kertoimista aritmeettisesti johdettua arvoa kutsutaan neliömatriisin determinantiksi. SciPy:ssä tämä voidaan tehdä funktiolla det, jonka syntaksi on seuraava:
SYNTAX:
det(a, overwrite_a=False, check_finite=True)
where,
a : (M, M) On neliömatriisi
overwrite_a( bool, valinnainen) : Sallii tietojen ylikirjoittamisen a:ssa
check_finite ( bool, valinnainen): Tarkistaa, koostuuko syötematriisi vain äärellisistä luvuista
ESIMERKKI:
import numpy as np
from scipy import linalg
A = np.array(, ])
B = linalg.det(A)
print(B)
TULOS: -5.0
Sparse Eigenvalues:
Eigenarvot ovat tietty joukko skalaareja, jotka liittyvät lineaarisiin yhtälöihin. ARPACK tarjoaa, että voit löytää ominaisarvot ( eigenvektorit ) melko nopeasti. ARPACKin koko toiminnallisuus on pakattu kahteen korkean tason rajapintaan, jotka ovat scipy.sparse.linalg.eigs ja scipy.sparse.linalg.eigsh. eigs. eigs-rajapinnan avulla voidaan löytää reaalisten tai kompleksisten epäsymmetristen neliömatriisien ominaisarvoja, kun taas eigsh-rajapinta sisältää rajapinnat reaalisymmetrisille tai kompleksis-hermitiläisille matriiseille.
Funktio eigh ratkaisee yleistetyn ominaisarvo-ongelman kompleksiselle hermeettiselle tai reaaliselle symmetriselle matriisille.
EXAMPLE:
from scipy.linalg import eigh
import numpy as np
A = np.array(, , , ])
a, b = eigh(A)
print("Selected eigenvalues :", a)
print("Complex ndarray :", b)
OUTPUT:
Valitut ominaisarvot :
Kompleksinen ndarray :
]
Spatiaaliset tietorakenteet ja algoritmit:
Spatiaalinen data koostuu periaatteessa objekteista, jotka koostuvat viivoista, pisteistä, pinnoista jne. SciPy:n scipy.spatial-paketilla voidaan laskea Voronoi-diagrammeja, kolmiomittauksia jne. käyttäen Qhull-kirjastoa. Se koostuu myös KDTree-toteutuksista lähimmän naapurin pistekyselyjä varten.
Delaunayn kolmiomuunnokset:
Matemaattisesti Delaunayn kolmiomuunnokset joukolle diskreettejä pisteitä tasossa on sellainen kolmiomuunnos, jonka mukaan yksikään piste kyseisessä pistejoukossa ei ole minkään kolmion kehäympyrän sisällä.
ESIMERKKI:
import matplotlib.pyplot as plt
from scipy.spatial import Delaunay
points = np.array(, , ,])
a = Delaunay(points) #Delaunay object
print(a)
print(a.simplices)
plt.triplot(points, points, a.simplices)
plt.plot(points, points, 'o')
plt.show()
TULOS:

Moniulotteiset kuvankäsittelytoiminnot:
Kuvankäsittelyn periaatteessa kyse on operaatioiden suorittamisesta kuvalla, jotta voidaan hakea informaatiota tai saada alkuperäisestä kuva parannettua. Scipy.ndimage-paketti koostuu useista kuvankäsittely- ja analyysitoiminnoista, jotka on suunniteltu työskentelemään mielivaltaisen ulottuvuuden omaavien matriisien kanssa.
Kehitys ja korrelaatio:
SciPy tarjoaa useita funktioita, jotka mahdollistavat kuvien korrelaation ja konvoluution.
- Funktiolla correlate1d voidaan laskea yksiulotteinen korrelaatio tiettyä akselia pitkin
- Funktiolla correlate voidaan laskea moniulotteinen korrelaatio mille tahansa tietylle joukolle määritetyllä ytimellä
- Funktiolla convolve1d voidaan laskea yksiulotteinen-moniulotteinen konvoluutio tiettyä akselia pitkin
- Funktio convolve mahdollistaa moniulotteisen konvoluution mille tahansa tietylle joukolle määritetyllä ytimellä
EHDOTUS:
import numpy as np
from scipy.ndimage import correlate1d
correlate1d(, weights=)
OUTPUT: array()
File IO:
The scipy.io -paketti tarjoaa useita funktioita, jotka auttavat sinua hallitsemaan eri muotoisia tiedostoja, kuten MATLAB-tiedostoja, IDL-tiedostoja, Matrix Market -tiedostoja jne.
Hyödyntääksesi tätä pakettia sinun on tuotava se seuraavasti:
import scipy.io as sio
Täydelliset tiedot alipaketista saat virallisesta asiakirjasta File IO.
Tällä päädymme tämän SciPy-oppaan loppuun. Toivottavasti olet ymmärtänyt kaiken selkeästi. Varmista, että harjoittelet mahdollisimman paljon.
Jos haluat lukea lisää artikkeleita markkinoiden trendikkäimmistä teknologioista, kuten tekoälystä, DevOpsista ja eettisestä hakkeroinnista, voit tutustua Edurekan viralliseen sivustoon.
Katso, että tässä sarjassa on tulossa muitakin artikkeleja, joissa kerrotaan Pythonin ja tietojenkäsittelytieteen muista näkökohdista.
1. Koneoppimisen luokittelija Pythonilla
2. Python Scikit-Learn Cheat Sheet
3. Koneoppimisen työkalut
4. Python-kirjastot datatieteeseen ja koneoppimiseen
5. Python-kirjastot datatieteeseen ja koneoppimiseen
. Chatbot In Python
6. Python Collections
7. Python Modules
8. Python developer Skills
9. Python developer Skills
. OOPs haastattelukysymykset ja vastaukset
10. Python-kehittäjän ansioluettelo
11. Tutkiva data-analyysi Pythonilla
12. Käärmepeli Pythonin kilpikonnamoduulilla
13. Python kehittäjä palkka
14. Pääkomponenttianalyysi
15. Python vs C++
16. Scrapy opetusohjelma
17. Web Scraping Pythonilla
18. Least Squares Regression Method
19. Jupyter Notebook Cheat Sheet
20. Pythonin perusteet
21. Python-malliohjelmat
22. Pythonin generaattorit
23. Python Decorator
24. Python Spyder IDE
25. Mobiilisovellukset Kivyn avulla Pythonissa
26. Top 10 parasta kirjaa oppia & harjoitella Python
27. Robot Framework Pythonilla
28. Käärmepeli Pythonilla PyGamen avulla
29. Djangon haastattelukysymykset ja vastaukset
30. Top 10 Python-sovellusta
31. Hash-taulukot ja Hashmaps Pythonissa
32. Python 3.8
33. Tukivektorikone
34. Python opetusohjelma