Miten ajatella eksponenttien ja logaritmien avulla

Tässä on temppu eksponentteja ja logaritmeja sisältävien ongelmien miettimiseen. Esitä vain kaksi kysymystä:

1) Puhummeko panoksista (muutoksen syy) vai tuotoksista (varsinainen tapahtunut muutos?)

Logaritmit paljastavat kasvun aiheuttaneet panokset
Eksponentit löytävät kasvun lopputuloksen

2) Puhummeko kasvattajan näkökulmasta vai havainnoitsijan näkökulmasta?

e ja luonnollinen logi ovat kasvattajan hetkellisestä näkökulmasta
Base 10, Base 2 jne. ovat ihmishavainnoitsijalle sopivia mittoja

Päässäni laitan vaihtoehdot taulukkoon:

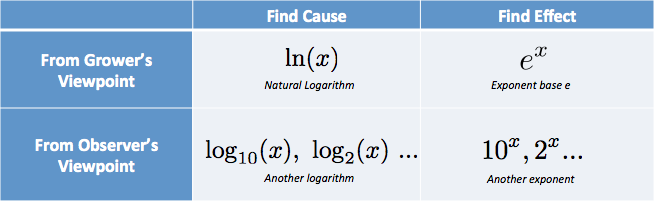
eksponentti logaritmi näkökulman vertailu

Minulla on ajatuksia tyyliin: ”Tarvitsen syyn, viljelijän näkökulmasta katsottuna… eli luonnollisen login.”. (Luonnollinen logaritmi lyhennetään pienellä LN:llä, korkealukuisesta logarithmus naturalis.)

Olin turhautunut luokkiin, joissa kuvattiin taulukon sisäistä osaa, raakafunktioita, ilman kuvatekstejä, joissa selitettiin, milloin niitä käytetään!”

Ei se onnistu, harjoitellaan suoraa ajattelua logaritmeilla ja eksponenteilla.”

Skenaario: BKT:n kasvun kuvaaminen

Tässä on tyypillinen esimerkki kasvusta:

Vuosina 2000-2010 Yhdysvaltain BKT muuttui 9,9 biljoonasta 14,4 biljoonaan

Ok, toki, nuo luvut osoittavat, että muutosta tapahtui. Mutta haluaisimme luultavasti näkemystä syyhyn: Millainen keskimääräinen vuotuinen kasvuvauhti selittäisi tämän muutoksen?

Aivoni ajattelevat heti ”logaritmeja”, koska työskentelemme takaperin kasvusta sen aiheuttaneeseen kasvuvauhtiin. Aloitan ajatuksen näin:

$\displaystyle{\text{muutoksen logaritmi} \rightarrow \text{kasvun syy} }$

Hyvä alku, mutta terävöitetään sitä.

Ensin, mitä logaritmia pitäisi käyttää?

Vakiossa valitsen luonnollisen logaritmin. Useimmat tapahtumat päätyvät kasvajan (ei havainnoitsijan) kannalta, ja tykkään ”ratsastaa” kasvavan elementin mukana visualisoidakseni, mitä tapahtuu. (Radiantit ovat samankaltaisia: ne mittaavat kulmia liikuttajan suhteen.)

Jatkokysymys: mihin muutokseen sovellamme logaritmia?

Olemme oikeastaan kiinnostuneita vain alun ja lopun välisestä suhteesta: 9,9 biljoonasta 14,4 biljoonaan kymmenessä vuodessa. Tämä on sama kasvuvauhti kuin siirtyminen \$9,90:stä \$14,40:een samassa ajassa.

Voidaan terävöittää ajatustamme:

$\displaystyle{\text{natural logarithm of growth ratio} \rightarrow \text{kasvun syy} }$

$\displaystyle{\ln(\frac{14.4}{9.9}) = .374}$

Ok, syynä oli 0,374 eli 37,4 %. Olemmeko valmiita?

Ei vielä. Logaritmit eivät tiedä, kuinka kauan muutos kesti (emmehän kytkeneet 10 vuotta?). Ne antavat meille nopeuden ikään kuin kaikki muutos tapahtuisi yhden ainoan ajanjakson aikana.

Muutos voi tosiaan olla yhden vuoden 37,4 %:n jatkuva kasvu, tai kahden vuoden 18,7 %:n kasvu, tai jokin muu yhdistelmä.

Skenaariosta tiedämme, että muutos kesti 10 vuotta, joten vauhdin on täytynyt olla:

$\displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3.74\%}$

Hetkittäisen, jatkuvan kasvun näkökulmasta USA:n talouskasvu on ollut 3,74 % vuodessa.

Vai olemmeko valmiit? Ei aivan!

Tämä jatkuva vauhti on kasvajan näkökulmasta, ikään kuin ”ratsastaisimme” talouden mukana sen muuttuessa. Pankkiiri varmaan välittää ihmisystävällisestä, vuositasolla tapahtuvasta erosta. Voimme selvittää tämän antamalla jatkuvan kasvun kulkea vuoden ajan:

$\displaystyle{\text{exponent with rate and time} \rightarrow \text{kasvun vaikutus} }$

$\displaystyle{e^{\text{rate} \cdot \text{time}} = \text{growth}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

Vuosikasvu on 3,8 %, mikä on hieman korkeampi kuin 3,74 %:n hetkellinen kasvuvauhti, joka johtuu korkokomponentista. Tässä on toinen tapa ilmaista asia:

Hetkittäin tarkasteltuna tietty osa taloudesta kasvaa 3,74 %, jota mallintaa $e^(.0374 * vuotta)$
Vuosikohtaisesti, kun yhdistelmävaikutukset on laskettu, talous kasvaa 3,81 %, mallinnettuna $1,0381^vuotta$

Taloudessa saatamme haluta vuosimuutoksen, jota voidaan mukavasti verrata muihin trendeihin. Tieteessä ja tekniikassa mallinnamme mieluummin käyttäytymistä hetkellisesti.

Skenaario: Luonnollisen kasvun kuvaaminen

Inhoan keksittyjä esimerkkejä kuten ”Oletetaan, että bakteeri kaksinkertaistuu 24 tunnin välein, etsi sen kasvukaava.”. Monistuvatko bakteeripesäkkeet puhtaiden ihmisten välein, ja odotammeko tarkkaa kaksinkertaistumista?

Parempi skenaario: ”Hei, löysin bakteereita, odotin tunnin, ja möykky kasvoi 2,3 grammasta 2,32 grammaan. Menen nyt lounaalle. Laske paljonko meillä on, kun palaan 3 tunnin päästä.”

Mallinnetaan tämä. Tarvitsemme logaritmin kasvunopeuden löytämiseksi ja sitten eksponentin kasvun ennustamiseksi eteenpäin. Kuten aiemminkin, pidetään kaikki aluksi luonnollisen logaritmin muodossa.

Kasvutekijä on:

$\displaystyle{\text{muutoksen logaritmi} \rightarrow \text{kasvun syy} }$

$\displaystyle{\ln(\text{kasvu}) = \ln(2.32/2.3) = .0086 = .86\%}$

Tämä on nopeus yhdeltä tunnilta, ja yleinen malli, jolla voidaan projisoida eteenpäin, on

$\displaystyle{\text{eksponentti, jossa on nopeus ja aika} \rightarrow \text{kasvun vaikutus} }$

$\displaystyle{e^{.0086 \cdot \text{hours}} \rightarrow \text{kasvun vaikutus} }$

Jos aloitamme 2.32:sta ja kasvamme 3 tuntia, saadaan:

$\displaystyle{2.32 \cdot e^{.0086 \cdot 3} = 2.38}$

Hauskuuden vuoksi, kauanko kestää, kunnes bakteeri kaksinkertaistuu? Kuvitellaan, että odotetaan, että 1 muuttuu 2:ksi:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hours}} = 2}$

Voimme mekaanisesti ottaa molempien puolien luonnollisen logaritmin ”kumotaksemme eksponentin”, mutta ajatellaanpa intuitiivisesti.

Jos 2 on lopputulos, niin ln(2) on kasvupanos, joka sai meidät sinne (jokin nopeus × aika). Tiedämme, että nopeus oli .0086, joten aika päästä 2:een olisi:

$\displaystyle{ \text{hours} = \frac{\ln(2)}{\text{rate}} = \frac{.693}{.0086} = 80.58}$

Yhdyskunta kaksinkertaistuu ~80 tunnin kuluttua. (Hyvä, ettet jäänyt paikalle?)

Mitä näkökulman muutos oikeasti tarkoittaa?

Sen selvittäminen, haluatko panoksen (kasvun syy) vai tuotoksen (kasvun tulos), on melko suoraviivaista. Mutta miten visualisoit kasvattajan näkökulman?

Kuvittele, että meillä on pieniä työläisiä, jotka rakentavat lopullista kasvumallia (ks. artikkeli eksponentit):

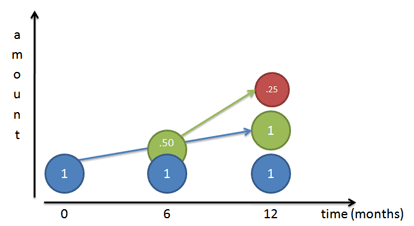
$korkokomponentti$

Jos kasvuvauhtimme on 100 %, käskemme alkuperäistä työläistämme (herra Sinistä) työskentelemään tasaisesti ja luomaan 100 %:n kopion itsestään vuoden loppuun mennessä. Jos seuraamme häntä päivä päivältä, huomaamme, että hän todellakin saa vuoden lopussa valmiiksi 100-prosenttisen kopion itsestään (herra Vihreä).

Mutta… se työntekijä, jota hän oli rakentamassa (herra Vihreä), alkaa myös työskennellä. Jos herra Green ilmestyy ensimmäisen kerran 6 kuukauden kohdalla, hänellä on puoli vuotta aikaa työskennellä (sama vuosivauhti kuin herra Blue) ja hän rakentaa herra Redin. Tietenkin herra Punainen jää lopulta puoliksi valmiiksi, koska herra Vihreällä on aikaa vain 6 kuukautta.

Entä jos herra Vihreä ilmestyisi paikalle 4 kuukauden kuluttua? Kuukauden kuluttua? Yhden päivän? Sekunnin? Jos työntekijät alkavat kasvaa välittömästi, saamme hetkestä toiseen -käyrän, jonka määrittelee $e^x$:

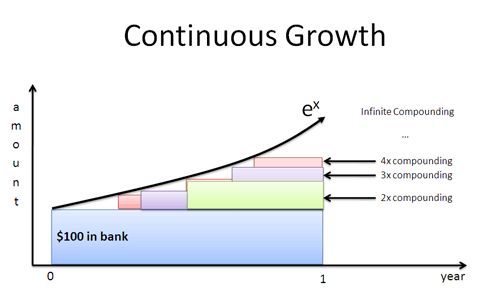
jatkuva kasvu

Luonnollinen logi antaa kasvunopeuden yksittäisen työntekijän näkökulmasta. Kytkemme tuon kasvuvauhdin $e^x$:iin löytääksemme lopputuloksen, johon on sisällytetty kaikki yhdysvaikutukset.

Muiden emästen käyttäminen

Vaihtaessamme toiseen logaritmityyppiin (emäksellä 10, emäksellä 2 jne.) etsimme jotakin kaavaa yleisessä kasvussa, emme sitä, mitä yksittäinen työntekijä tekee.

Jokainen logaritmi kysyy kysymyksen nähdessämme muutosta:

Login emäksellä e: Mikä oli kunkin työntekijän noudattama hetkellinen vauhti?
Log base 2: Kuinka monta tuplausta tarvittiin?
Log base 10: Kuinka monta 10x-ystä tarvittiin?

Tässä on analysoitava skenaario:

Tyypillisten sirujen transistorimäärät kasvoivat 30 vuoden aikana 1000:sta 1 miljardiin

Miten analysoisit tämän?

Mikrosirut eivät ole mikään yhtenäinen kokonaisuus, joka kasvaisi tasaisesti ajan myötä. Ne ovat erillisiä painoksia, kilpailevilta yrityksiltä, ja ne kertovat yleisestä teknologiatrendistä.
Koska emme ole ”ratsastamassa” kasvavan mikrosirun mukana, käyttäkäämme asteikkoa, joka on tehty ihmisten mukavuuden vuoksi. Kaksinkertaistaminen on helpompi ajatella kuin kymmenkertaistaminen.

Tällaisilla oletuksilla saamme:

$\displaystyle{\text{logarithm of change} \rightarrow \text{kasvun syy} }$

$\displaystyle{\log_2(\frac{\text{1 miljardi}}{1000}) = \log_2(\text{1 miljoona}) \sim \text{20 kaksinkertaistumista}}$

”Kasvun syy” oli 20 kaksinkertaistumista, joiden tiedämme tapahtuneen 30 vuoden aikana. Tämä tarkoittaa keskimäärin 2/3 kaksinkertaistumista vuodessa eli 1,5 vuotta per kaksinkertaistuminen – mukava nyrkkisääntö.

Kasvattajan näkökulmasta laskisimme $\ln(\text{1 miljardi}/1000) / \text{30 vuotta} = 46\%$ jatkuvasta kasvusta (hieman vaikeampi suhteuttaa tähän skenaarioon).

Voidaan tiivistää analyysimme taulukkoon:

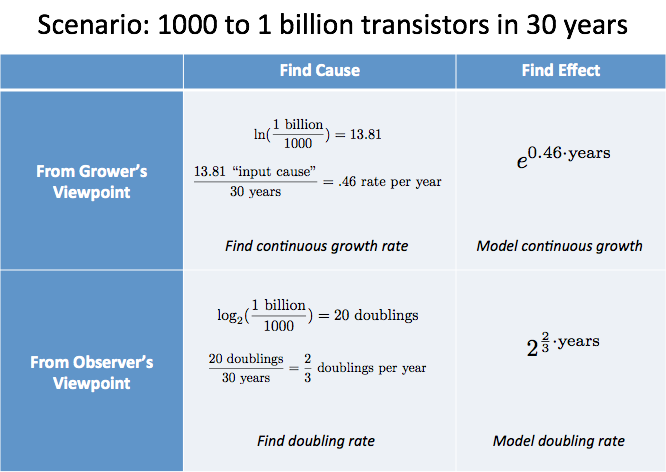
eksponentit transistori esimerkki

Yhteenveto

Oppimisessa on kyse siitä, että löydämme käsitteen taakse kätketyt kuvatekstit. Milloin sitä käytetään? Minkä näkökulman se tuo ongelmaan?

Tämänhetkinen tulkintani on, että eksponentit kysyvät syy vs. seuraus ja kasvattaja vs. tarkkailija. Mutta emme ole koskaan valmiita; osa hauskuutta on nähdä, miten voimme uudelleenkirjoittaa vanhoja käsitteitä.

Hyvää matematiikkaa.

Liite: The Change Of Base Formula

Tässä on miten ajatella emäksen vaihtamista. Olettaen 100 %:n jatkuvan kasvunopeuden,

ln(x) on aika kasvaa x:ksi
ln(2) on aika kasvaa 2:ksi

Koska meillä on aika kaksinkertaistua, voimme katsoa kuinka monta ”mahtuisi” kokonaisaikaan kasvaa x:ksi:

$\displaystyle{\text{number of doublings from 1 to x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

Kuinkahan monta kaksinkertaistumista tapahtuu esimerkiksi 1:stä 64:ään?

Noh, ln(64) = 4,158. Ja ln(2) = .693. Sopivien kaksinkertaistumisten määrä on:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4.158}{.693} = 6}$

Todellisessa maailmassa laskimet saattavat menettää tarkkuuttaan, joten käytä suoraa log-perustan 2 funktiota, jos mahdollista. Ja tietysti meillä voi olla murtoluku: Pääseminen 1:stä 2:n neliöjuureen on ”puolet” kaksinkertaistumisesta eli log2(1,414) = 0,5.

Vaihtaessamme log-perustaan 10 tarkoitamme, että laskemme sopivien 10x-lukujen määrän:

$\displaystyle{\text{number of 10x-lukujen määrä 1:stä x:ään} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Kiva, eikö? Lue lisää esimerkkejä lukemalla Logaritmien käyttö reaalimaailmassa.

Tämän sarjan muut viestit

Intuitiivinen opas eksponenttifunktioihin & e
Naturaalilogaritmin (ln)
Visuaalinen opas yksinkertaisiin, yhdistettyihin ja jatkuviin korkokantoihin
Yleisiä e:n määritelmiä (väriteltyinä)
Ymmärtää eksponentteja (Miksi 0^0 = 1?)
Logaritmien käyttäminen reaalimaailmassa
Miten ajatella eksponenttien ja logaritmien avulla
Diskreetin vs. jatkuvan kasvun ymmärtäminen
Mitä eksponentti oikeasti tarkoittaa?
Kysymys: Miksi e on erityinen? (2,718…, eikä 2, 3,7 tai jokin muu luku?)