How to Prepare for the Geometry Questions on Matematiikan kokeessa
Geometrian opinto-opas matematiikan perusteisiin
Geometria on vain hieno nimi viivojen ja muotojen tutkimiselle. On varmasti muitakin vaikeita periaatteita ja aiheita, mutta meillä on tässä perusasiat. Sinun on hallittava nämä ennen kuin käsittelet edistyneempiä käsitteitä.
(Huomaa, että jos kuvio on tässä oppaassa merkitty ”esimerkkinä”, se ei välttämättä ole ainoa esitys kyseisestä kuviosta, mutta se on yksi niistä.)
Pisteet ja viivat
Piste geometriassa on paikka. Sillä ei ole pituutta, leveyttä tai syvyyttä. Käytämme pistettä ja isoa kirjainta osoittamaan pistettä.
Viivasegmentti määritellään kahdesta pisteestä ja kaikista niiden välisistä pisteistä. Näitä kahta pistettä kutsutaan segmentin päätepisteiksi. Segmentillä on yksi ulottuvuus: pituus. Jos haluat kirjoittaa segmentin, aseta viiva kahden päätepisteen päälle. \(\overline{AB}\) tai \(\overline{BA}\) on tämä segmentti:

Viiva ulottuu molempiin suuntiin ilman loppua. Voit kirjoittaa viivan asettamalla kahden nuolen muodostaman palkin minkä tahansa viivan kahden pisteen päälle. \(\overleftrightarrow{AB}\) tai \(\overleftrightarrow{BA}\) on viiva:

Säde alkaa yhdestä päätepisteestä ja ulottuu päättymättä vain yhteen suuntaan. Kun haluat kirjoittaa säteen, aseta oikealle osoittavalla nuolella varustettu palkki kahden pisteen päälle: päätepisteen ja minkä tahansa muun pisteen (kyseisessä suunnassa). \(\overrightarrow{AB}\) on säde:

Huomaa: sädettä ei voi kirjoittaa niin, että nuoli osoittaa vasemmalle kuten \(\overleftarrow{BA}\). Myös järjestys on tärkeä. \(\overrightarrow{BA}\) ei ole sama kuin \(\overrightarrow{AB}\). Ensimmäinen kirjain on aina säteen alkupiste.
Kaksi viivaa, segmenttiä tai sädettä ovat kohtisuorassa, jos ne muodostavat suoran kulman (ks. alla). Käytä symbolia \(\perp\) merkitsemään kohtisuoruutta. Jos esimerkiksi \(\overline{AB}\) on kohtisuorassa \(\overline{CD}\), voit kirjoittaa \(\overline{AB} \perp \overline{CD}\).
Esimerkkejä: 
Kaksi suoraa ovat yhdensuuntaisia, jos ne eivät koskaan leikkaa toisiaan. Jos \(\ylioikea{AB}\) on yhdensuuntainen \(\ylioikea{CD}\) kanssa, voidaan kirjoittaa \(\ylioikea{AB} \paralleeli \ylioikea{CD}\).
Examples: 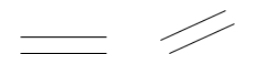
Tasomuodot
Geometriassa taso on tasainen kaksiulotteinen pinta, joka ulottuu äärettömän kauas. Nämä kaksi ulottuvuutta ovat pituus ja leveys. Tasomuodot ovat siis ”litteitä” muotoja, kuten neliöt, ympyrät ja kolmiot.
Yleiset muodot
Monikulmio on tasossa sijaitseva suljettu pinta, jota rajoittavat viivapätkät, joita kutsutaan sivuiksi.
Esimerkkejä: 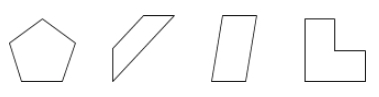
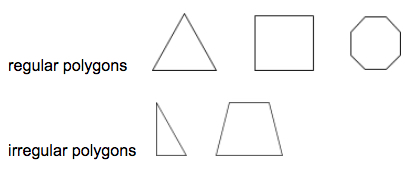
Säännöllinen monikulmio on monikulmio, jossa kaikki segmentit ja sisäkulmat ovat yhteneviä.
Esimerkkejä:
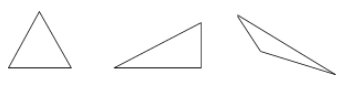
Kolmio on kolmisivuinen monikulmio.
Esimerkkejä:
Nelikulmiot – nelisivuiset monikulmiot
Paralleelogrammi on nelikulmiotyyppi, jonka vastakkaiset sivut ovat yhdensuuntaiset ja yhtenevät. Myös parallelogrammin vastakkaiset kulmat ovat yhteneviä.
Esimerkkejä: 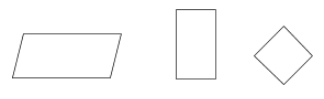
Suorakulmio on parallelogrammi, jolla on neljä suoraa kulmaa.
Esimerkkejä: 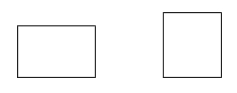
Rombi on parallelogrammi, jonka kaikki neljä sivua ovat yhtenevät.
Esimerkkejä: 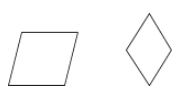
Neliö on parallelogrammi, joka on sekä rombi että suorakulmio (kaikki sivut ovat yhteneviä ja kaikki kulmat oikeita).
Esimerkkejä: 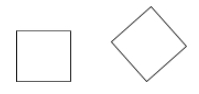
Trapetsoidi on nelikulmio, jossa on vain yksi pari yhdensuuntaisia sivuja.
Esimerkkejä: 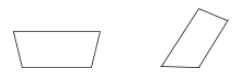
Polygonit, joissa on enemmän kuin neljä sivua
\
\(^1\) Monikulmiota, jossa on 11 sivua, voidaan kutsua myös endekagoniksi tai epädekagoniksi.
Mittaamalla muotoja
Ympyrän ympärysmitta on monikulmion ympärillä kulkeva kokonaismatka. Kehä saadaan selville laskemalla yhteen kaikkien sivujen pituudet. Jos monikulmio on säännöllinen (kaikki sivut ovat yhteneviä) ja yhden sivun pituus on \(s\), kerro sivujen lukumäärä \(s\):llä, niin löydät kehän. Esimerkiksi säännöllisen viisikulmion ympärysmitta on \(P_\text{reg pentagon}=5s\)
.