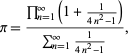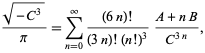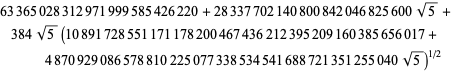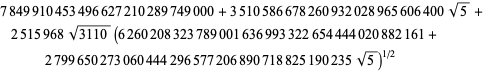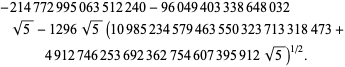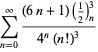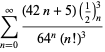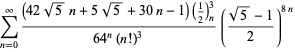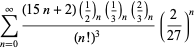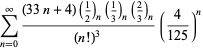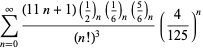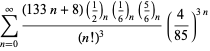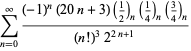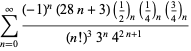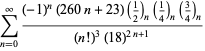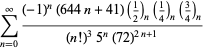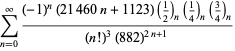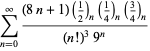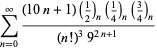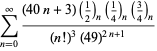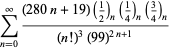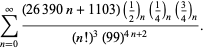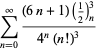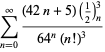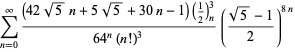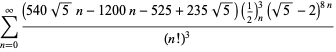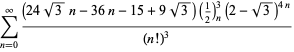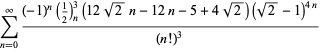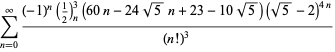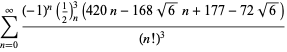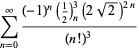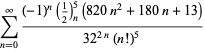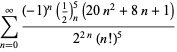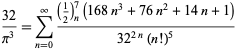Piin kaavat

Posted on by admin
Lukuteoria > Vakiot > Pii >
Laskutoimitukset ja analyysi > Sarjat > BBP-kaavat >
Laskutoimitukset ja analyysi > Laskutoimitukset > Laskutaito > Integraalit > Määrätyt integraalit >
MathWorld Contributors > Cloitre >
MathWorld Contributors > Plouffe >
MathWorld Contributors > Sondow >

Less…

DOWNLOAD Mathematica Notebook

Monentyyppisiä kaavoja pi on monia. Näitä ovat muun muassa sarjat, tuotteet, geometriset konstruktiot, raja-arvot, erikoisarvot ja pii-iteraatiot.

pi liittyy läheisesti ympyrän ja pallon ominaisuuksiin. Ympyrälle, jonka säde on r, kehä ja pinta-ala saadaan

A

C = 2pir
(1)
A C pir^2.
(2)

Säteeltään r pallolle vastaavasti, suljettu pinta-ala ja tilavuus ovat

.

S = 4pir^2
(3)
V = 4/3pir^3.
(4)

Tarkka kaava pi yksikkömurtolukujen käänteistangenttien suhteen on Machinin kaava

1/4pi=4tan^(-1)(1/5)-tan^(-1)(1/(239)).
(5)

On olemassa kolme muuta Machinin kaltaista kaavaa,sekä tuhansia muita samankaltaisia kaavoja,joissa on enemmän termejä.

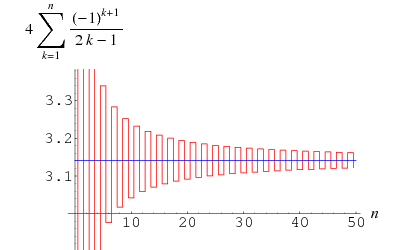
GregorySeries

Gregory ja Leibniz löysivät

pi/4 = sum_(k=1)^(infty)((-1)^(k+1))/(2k-1)
(6)
= 1-1/3+1/5-...
(7)

(Wells 1986, s. 50), joka tunnetaan Gregory-sarjana ja joka saadaan liittämällä x=1 Leibnizin sarjaan tan^(-1)x. Virhe tämän Gregory-sarjan n:nnen termin jälkeen on suurempi kuin (2n)^(-1), joten tämä summa konvergoi niin hitaasti, että 300 termiä ei riitä laskemaan pi oikein kahden desimaalin tarkkuudella! Se voidaan kuitenkin muuntaa muotoon

pi=summa_(k=1)^infty(3^k-1)/(4^k)zeta(k+1),
(8)

jossa zeta(z) on Riemannin zeta-funktio (Vardi 1991, s. 157-158; Flajolet ja Vardi 1996), joten virhe k termien jälkeen on n. (3/4)^k.

Abraham Sharpille (n. 1717) saadaan

pi=sum_(k=0)^infty(2(-1)^k3^(1/2-k))/(2k+1)
(9)

(Smith 1953, s. 311). Muita yksinkertaisia sarjoja, joissa pi esiintyy, ovat

.

1/4pisqrt(2) = summa_(k=1)^(infty)
(10)
= 1+1/3-1/5-1/7+1/9+1/(11)-...
(11)
1/4(pi-3) = sum_(k=1)^(infty)((-1)^(k+1))/(2k(2k+1)(2k+2))
(12)
= 1/(2-3-4)-1/(4-5-6)+1/(6-7-8)-...
(13)
1/6pi^2 = sum_(k=1)^(infty)1/(k^2)
(14)
= 1+1/4+1/9+1/(16)+1/(25)+...
(15)
1/8pi^2 = sum_(k=1)^(infty)1/((2k-1)^2)
(16)
= 1+1/(3^2)+1/(5^2)+1/(7^2)+...
(17)

(Wells 1986, s. 53).

Vuonna 1666, Newton johti geometrisen konstruktion avulla kaavan

pi = 3/4sqrt(3)+24int_0^(1/4)sqrt(x-x^2)dx
(18)
= (3sqrt(3))/4+24(1/(12)-1/(5-2^5)-1/(28-2^7)-1/(72-2^9)-...),
(19)

jota hän käytti pi laskemiseen (Wells 1986, s. 50; Borwein et al. 1989; Borwein ja Bailey 2003, s. 105-106). Kertoimet löytyvät integraalista

I(x) = intsqrt(x-x^2)dx
(20)
= 1/4(2x-1)sqrt(x-x^2)-1/8sin^(-1)(1-2x)
(21)

mennessä sarjalaajennusta I(x)-I(0) 0:n ympäri, obtaining

I(x)=2/3x^(3/2)-1/5x^(5/2)-1/(28)x^(7/2)-1/(72)x^(9/2)-5/(704)x^(11/2)+...
(22)

(OEIS A054387 ja A054388). Käyttämällä Eulerin konvergenssin parantamismuunnosta saadaan

pi/2 = 1/2sum_(n=0)^(infty)((n!)^22^(n+1))/((2n+1)!)=sum_(n=0)^(infty)(n!)/((2n+1)!!!)
(23)
= 1+1/3+(1-2)/(3-5)+(1-2-3)/(3-5-7)+...
(24)
= 1+1/3(1+2/5(1+3/7(1+4/9(1+...))))
(25)

(Beeler et al. 1972, kohta 120).

Tämä vastaa liittämistä x=1/sqrt(2) hypergeometrisen funktion _2F_1(a,b;c;x),

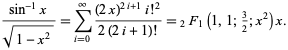(sin^(-1)x)/(sqrt(1-x^2))=sum_(i=0)^infty((2x)^(2i+1)i!^2)/(2(2i+1)!)=_2F_1(1,1;3/2;x^2)x.
(26)

Konvergenssin paranemisesta huolimatta sarja (◇) konvergoi vain yhdellä bitillä/termi. Neliöjuuren kustannuksella Gosper on todennut, että x=1/2 antaa 2 bittiä/termi,

1/9sqrt(3)pi=1/2sum_(i=0)^infty((i!)^2)/((2i+1)!),
(27)

ja x=sin(pi/10) antaa lähes 3.39 bittiä/termi,

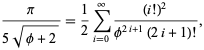pi/(5sqrt(phi+2))=1/2sum_(i=0)^infty((i!)^2)/(phi^(2i+1)(2i+1)!),
(28)

jossa phi on kultainen leikkaus. Gosper sai myös

pi=3+1/(60)(8+(2-3)/(7-8-3)(13+(3-5)/(10-11-3)(18+(4-7)/(13-14-3)(23+...)))).
(29)

Rabinowitz ja Wagon (1995; Borwein ja Bailey 2003, s. 141-142) esittävät spigot-algoritmin pi:lle.

Hämmästyttävämpää on, että Bailey et al. löysivät suljetussa muodossa olevan lausekkeen, joka antaa numeronlouhinta-algoritmin, joka tuottaa numerot pi (tai pi^2) emäksellä 16. (Bailey et al. 1997, Adamchik ja Wagon 1997),

pi=sum_(n=0)^infty(4/(8n+1)-2/(8n+4)-1/(8n+5)-1/(8n+6)-1/(8n+6))(1/(16))^n.
(30)

Tämä BBP-kaavana tunnettu kaava löydettiin PSLQ-algoritmin avulla (Ferguson et al. 1999) ja se vastaa

pi=int_0^1(16y-16)/(y^4-2y^3+4y-4)dy.
(31)

On olemassa sarja BBP-tyyppisiä kaavoja pi:lle (-1)^k potensseina, joiden ensimmäiset itsenäiset kaavat ovat

pi = 4sum_(k=0)^(infty)((-1)^k)/(2k+1)
(32)
= 3sum_(k=0)^(infty)(-1)^k
(33)
= 4sum_(k=0)^(infty)(-1)^k
(34)
= sum_(k=0)^(infty)(-1)^k
(35)
= sum_(k=0)^(infty)(-1)^k
(36)
= sum_(k=0)^(infty)(-1)^k.
(37)

Seuraavasti on olemassa sarja BBP-tyyppisiä kaavoja pi:lle 2^k potensseina, joista ensimmäiset riippumattomat kaavat ovat

pi = sum_(k=0)^(infty)1/(16^k)
(38)
= 1/2sum_(k=0)^(infty)1/(16^k)
(39)
= = 1/(16)sum_(k=0)^(infty)1/(256^k)
(40)
= 1/(32)sum_(k=0)^(infty)1/(256^k)
(41)
= 1/(32)sum_(k=0)^(infty)^(4096^k)1/(4096^k)
(42)
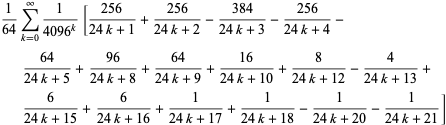= 1/(64)sum_(k=0)^(infty)1/(4096^k)
(43)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(44)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(45)
= 1/(96)sum_(k=0)^(infty)1/(4096^k)
(46)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k)
(47)
= 1/(4096)sum_(k=0)^(infty)1/(65536^k).
(48)

F. Bellard löysi nopeasti konvergoivan BBP-tyyppikaavan

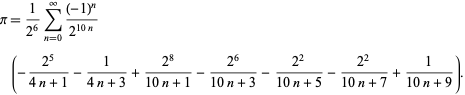pi=1/(2^6)sum_(n=0)^infty((-1)^n)/(2^(10n))(-(2^5)/(4n+1)-1/(4n+3)+(2^8)/(10n+1)-(2^6)/(10n+3)-(2^2)/(10n+5)-(2^2)/(10n+7)+1/(10n+9)).
(49)

Seuraava integraali on

pi=(22)/7-int_0^1(x^4(1-x)^4)/(1+x^2)dx
(50)

(Dalzell 1944, 1971; Le Lionnais 1983, s. 22; Borwein, Bailey ja Girgensohn 2004, s. 3; Boros ja Moll 2004, s. 125; Lucas 2005; Borwein ym. 2007, s. 14). K. Mahler tunsi tämän integraalin 1960-luvun puolivälissä, ja se esiintyy Sydneyn yliopiston tentissä marraskuussa 1960 (Borwein, Bailey ja Girgensohn, s. 3). Beukers (2000) sekä Boros ja Moll (2004, s. 126) toteavat, että ei ole selvää, onko näistä olemassa luonnollinen valinta rationaaliselle polynomille, jonka integraali 0:n ja 1:n välillä tuottaa pi-333/106, jossa 333/106 on seuraava konvergentti. Neljännelle konvergentille on kuitenkin olemassa integraali, nimittäin

pi=(355)/(113)-1/(3164)int_0^1(x^8(1-x)^8(25+816x^2))/(1+x^2)dx.
(51)

(Lucas 2005; Bailey et al. 2007, s. 219). Itse asiassa Lucas (2005) antaa muutamia muitakin tällaisia integraaleja.

Backhouse (1995) käytti identiteettiä

I_(m,n) = int_0^1(x^m(1-x)^n)/(1+x^2)dx
(52)
= 2^(-(m+n+1))sqrt(pi)Gamma(m+1)Gamma(n+1)×_3F_2(1,(m+1)/2,(m+2)/2;(m+n+2)/2,(m+n+3)/2;-1)
(53)
= a+bpi+cln2
(54)

positiivisille kokonaisluvuille m ja n ja missä a, b ja c ovat rationaalivakioita, joiden avulla voidaan tuottaa joukko kaavoja pi:lle. Erityisesti jos 2m-n=0 (mod 4), niin c=0 (Lucas 2005).

Sittemmin Ferguson löysi samanlaisen kaavan, mikä johti tällaisten kaavojen kaksiulotteiseen ristikkoon, joka voidaan tuottaa näillä kahdella kaavalla, jotka saadaan

pi=sum_(k=0)^infty((4+8r)/(8k+1)-(8r)/(8k+2)-(4r)/(8k+3)-(2+8r)/(8k+4)-(1+2r)/(8k+5)-(1+2r)/(8k+6)+r/(8k+7))(1/(16))^k
(55)

mille tahansa kompleksiselle r:n arvolle (Adamtshik ja Vaunu), jolloin BBP-kaava on erikoistapaus r=0.

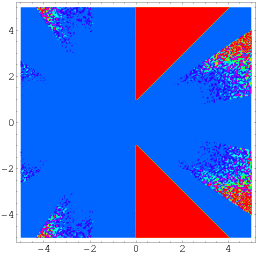
PiFormulasWagonIdentity

Wagonista johtuva vielä yleisempi identiteetti saadaan

pi+4tan^(-1)z+2ln((1-2z-z^2)/(z^2+1))=sum_(k=0)^infty1/(16^k)
(56)

(Borwein ja Bailey 2003, p. 141), joka pätee kompleksitason alueella, joka ei sisällä kahta reaalisen akselin suhteen symmetrisesti sijoitettua kolmion osaa, kuten edellä on esitetty.

Mahdollisesti vielä oudomman yleisen identiteettiluokan antaa

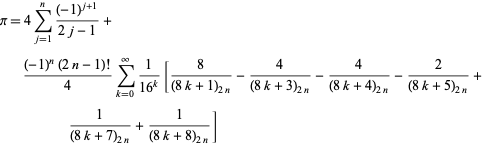pi=4sum_(j=1)^n((-1)^(j+1))/(2j-1)+((-1)^n(2n-1)!)/4sum_(k=0)^infty1/(16^k)
(57)

joka pätee mille tahansa positiiviselle kokonaisluvulle n, missä (x)_n on Pochhammerin symboli (B. Cloitre, pers. comm.., Jan. 23, 2005). Vielä hämmästyttävämpää on, että 2:n luonnolliselle logaritmille on olemassa läheisesti analoginen kaava.

Kun 16-lukulaisen BBP-kaavan ja siihen liittyvien kaavojen löytämisen jälkeen tutkittiin vastaavia kaavoja muissa emäksissä. Borwein, Bailey ja Girgensohn (2004) ovat hiljattain osoittaneet, että pi:llä ei ole Machin-tyyppistä BBP-arktangenttikaavaa, joka ei olisi binäärinen, vaikkakaan tämä ei sulje pois sitä, että muissa emäksissä käytettäisiin täysin erilaista skeemaa lukujen louhinta-algoritmeja.

S. Plouffe on kehittänyt algoritmin, jolla voidaan laskea pi:n n:nnen luvun pi:n n:nnen luvun n:nnen luvun n:nnen luvun n:nnen luvun pi:n n:nnen luvun n:nnen luvun n:nnen luvun n:nnen luvun pi:n n:nnen luvun laskemiseksi millä tahansa emäksellä, missä tahansa emäksellä ja O(n^3(logn)^3):n askeleella. Ramanujan löysi

sum_(k=0)^infty((-1)^k(4k+1)^3)/(^3)=sum_(k=0)^infty((-1)^k(4k+1)^3)/(pi^(3/2)^3)=2/pi
(58)

(Hardy 1923, 1924, 1999, p. 7).

Plouffe (2006) löysi kauniin kaavan

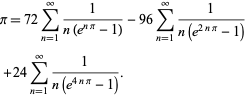pi=72sum_(n=1)^infty1/(n(e^(npi)-1))-96sum_(n=1)^infty1/(n(e^(2npi)-1)) +24sum_(n=1)^infty1/(n(e^(4npi)-1)).
(59)

PiBlatnerProduct

Eulerilta peräisin oleva mielenkiintoinen äärettömän tulon kaava, joka yhdistää pi ja n:nnen alkuluvun p_n, on

.

pi = 2/(tuote_(n=1)^(infty))
(60)
= 2/(product_(n=2)^(infty))
(61)

(Blatner 1997, p. 119), joka on piirretty edellä tuotteen termien lukumäärän funktiona.

Arkimedeksen menetelmää muistuttavaa menetelmää voidaan käyttää pi arvioimiseen aloittamalla n-gonista ja suhteuttamalla sitten seuraavien 2n-gonien pinta-alat. Olkoon beta kulma yhden monikulmion segmentin keskipisteestä,

beta=1/4(n-3)pi,
(62)

ton

pi=(2sin(2beta))/((n-3)product_(k=0)^(infty)cos(2^(-k)beta)))
(63)

(Beckmann 1989, pp. 92-94).

Vieta (1593) antoi ensimmäisenä tarkan lausekkeen pi:lle ottamalla yllä olevaan lausekkeeseen n=4, jolloin

cosbeta=sinbeta=1/(sqrt(2))=1/2sqrt(2),
(64)

mikä johtaa sisäkkäisten radikaalien äärettömään tuotteeseen,

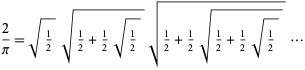2/pi=sqrt(1/2)sqrt(1/2+1/2sqrt(1/2))sqrt(1/2+1/2sqrt(1/2+1/2sqrt(1/2))...
(65)

(Wells 1986, s. 50; Beckmann 1989, s. 95). Tämän lausekkeen konvergenssi todistettiin kuitenkin tiukasti vasta Rudion vuonna 1892.

Seuraava kaava saadaan

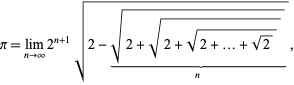pi=lim_(n-infty)2^(n+1)sqrt(2-sqrt(2+sqrt(2+sqrt(2+sqrt(2+....+sqrt(2))))_()_(n)),
(66)

joka voidaan kirjoittaa

pi=lim_(n-infty)2^(n+1)pi_n,
(67)

jossa pi_n määritellään iteraation

avulla

pi_n=sqrt((1/2pi_(n-1))^2+^2)
(68)

kanssa pi_0=sqrt(2) (J. Munkhammar, henkilökohtainen tiedonanto, 27. huhtikuuta 2000). Kaava

pi=2lim_(m-infty)sum_(n=1)^msqrt(^2+1/(m^2))
(69)

liittyy myös läheisesti.

Nätti kaava pi:lle saadaan

pi=(product_(n=1)^(infty)(1+1/(4n^2-1)))/(sum_(n=1)^(infty)1/(4n^2-1)),
(70)

jossa osoittaja on Wallisin kaavan muoto pi/2 ja nimittäjä on teleskooppisumma, jonka summa on 1/2, koska

1/(4n^2-1)=1/2(1/(2n-1)-1/(2n+1))
(71)

(Sondow 1997).

Wallisin kaavan erityistapaus antaa

pi/2=tuote_(n=1)^infty=(2-2)/(1-3)(4-4)/(3-5)(6-6)/(5-7)...
(72)

(Wells 1986, s. 50). Tämä kaava voidaan kirjoittaa myös

lim_(n-infty)(2^(4n))/(n(2n; n)^2)=pilim_(n-infty)(n^2)/(^2)=pi,
(73)

jossa (n; k) tarkoittaa binomikerrointa ja Gamma(x) on gammafunktio (Knopp 1990). Euler sai

pi=sqrt(6(1+1/(2^2)+1/(3^2)+1/(4^2)+....)),
(74)

mikä seuraa Riemannin zeta-funktion erityisarvosta zeta(2)=pi^2/6. Vastaava kaava seuraa zeta(2n):stä kaikille positiivisille kokonaisluvuille n.

Ramanujanin johtama ääretön summa on

1/pi=sum_(n=0)^infty(2n; n)^3(42n+5)/(2^(12n+4))
(75)

(Borwein et al. 1989; Borwein ja Bailey 2003, s. 109; Bailey et al.2007, s. 44). Lisää summia on esitetty Ramanujanin (1913-14),

4/pi=sum_(n=0)^infty((-1)^n(1123+21460n)(2n-1)!!(4n-1)!!)/(882^(2n+1)32^n(n!)^3)
(76)

ja

1/pi = sqrt(8)sum_(n=0)^(infty)((1103+26390n)(2n-1)!!(4n-1)!!)/(99^(4n+2)32^n(n!)^3)
(77)
= (sqrt(8))/(9801)sum_(n=0)^(infty)((4n)!(1103+26390n))/((n!)^4396^(4n))
(78)

(Beeler et al. 1972, kohta 139; Borwein et al. 1989; Borwein ja Bailey 2003, s. 108; Bailey et al. 2007, s. 44). Yhtälö (78) on johdettu modulaarisesta identiteetistä, jonka järjestys on 58, vaikka ensimmäistä derivaatiota ei esitetty ennen Borweinia ja Borweinia (1987). Edellä mainitut sarjat antavat molemmat

pi approx (9801)/(2206sqrt(2))=3.14159273001...
(79)

(Wells 1986, s. 54) ensimmäisenä approksimaationa ja antaa vastaavasti noin 6 ja 8 desimaalia per termi. Tällaisia sarjoja on olemassa erilaisten modulaaristen invarianttien järkevyyden vuoksi.

Sarjan yleinen muoto on

sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)1/(^n)=(sqrt(-j(t)))/pi,
(80)

jossa t on binäärisen kvadraattisen muodon diskriminantti, j(t) on j-funktio,

.

b(t) = sqrt(t)
(81)
a(t) = (b(t))/6{1-(E_4(t))/(E_6(t))},
(82)

ja E_i ovat Eisensteinin sarjoja. Luokkanumerokenttään p kuuluvat pkolmannen asteen algebralliset kokonaisluvut vakiot A=a(t), B=b(t) ja C=c(t). Kaikista pelkistä kokonaislukutermistä koostuvista sarjoista se, joka antaa lyhimmässä ajassa eniten numerolukuja, vastaa suurinta luokan numero 1 diskriminanttia d=-163, jonka Chudnovskyn veljekset (1987) muotoilivat. Tässä esiintyvä 163 on sama, joka esiintyy siinä, että e^(pisqrt(163)) (Ramanujanin vakio) on hyvin lähellä kokonaislukua. Vastaavasti tekijä 640320^3 tulee j-funktion identiteetistä j(1/2(1+isqrt(163))). Sarja saadaan

1/pi = 12sum_(n=0)^(infty)((-1)^n(6n)!(13591409+545140134n))/((n!)^3(3n)!(640320^3)^(n+1/2))
(83)
= (163·8·27·7·11·19·127)/(640320^(3/2))sum_(n=0)^(infty)((13591409)/(163·2·9·7·11·19·127)+n)((6n)!)/((3n)!(n!)^3)((-1)^n)/(640320^(3n))
(84)

(Borwein ja Borwein 1993; Beck ja Trott; Bailey et al. 2007, s. 44). Tämä sarja antaa 14 numeroa tarkasti per termi. Saman yhtälön toisessa muodossa antoivat Chudnovskyn veljekset (1987), ja Wolfram Language käyttää sitä pi laskemiseen (Vardi 1991; Wolfram Research),

pi=(426880sqrt(10005))/(A),
(85)

missä

A = 13591409
(86)
B = -1/(151931373056000)
(87)
C = (30285563)/(1651969144908540723200).
(88)

Luokan numero 2 (suurin diskriminantti -427) paras kaava on

1/pi=12sum_(n=0)^infty((-1)^n(6n)!(A+Bn))/((n!)^3(3n)!C^(n+1/2)),
(89)

missä

A = = 212175710912sqrt(61)+1657145277365
(90)
B = 13773980892672sqrt(61)+107578229802750
(91)
C = ^3
(92)

(Borwein ja Borwein 1993). Tämä sarja lisää noin 25 numeroa jokaista ylimääräistä termiä kohti. Nopeimmin konvergoiva sarja luokalle numero 3 vastaa d=-907 ja antaa 37-38 numeroa per termi. Nopeimmin konvergoiva luokan numero 4 sarja vastaa d=-1555 ja on

(sqrt(-C^3))/pi=sum_(n=0)^infty((6n)!)/((3n)!(n!)^3)(A+nB)/(C^(3n)),
(93)

missä

A = 63365028312971999585426220+28337702140800842046825600sqrt(5)+384sqrt(5)(10891728551171178200467436212395209160385656017+4870929086578810225077338534541688721351255040sqrt(5))^(1/2)
(94)
B = 7849910453496627210289749000+3510586678260932028965606400sqrt(5)+2515968sqrt(3110)(6260208323789001636993322654444020882161+2799650273060444296577206890718825190235sqrt(5))^(1/2)
(95)
C = -214772995063512240-96049403338648032sqrt(5)-1296sqrt(5)(10985234579463550323713318473+4912746253692362754607395912sqrt(5))^(1/2).
(96)

Tämä antaa 50 numeroa per termi. Borwein ja Borwein (1993) ovat kehittäneet yleisen algoritmin tällaisten sarjojen generoimiseksi mielivaltaiselle luokkamäärälle.

Kokonaisen luettelon Ramanujanin toisesta ja kolmannesta muistikirjasta löytyvistä sarjoista luvulle 1/pi antaa Berndt (1994, pp. 352-354),

4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(97)
(16)/pi = sum_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(98)
(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(99)
(27)/(4pi) = sum_(n=0)^(infty)((15n+2)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(2/(27))^n
(100)
(15sqrt(3))/(2pi) = sum_(n=0)^(infty)((33n+4)(1/2)_n(1/3)_n(2/3)_n)/((n!)^3)(4/(125))^n
(101)
(5sqrt(5))/(2pisqrt(3)) = sum_(n=0)^(infty)((11n+1)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(125))^n
(102)
(85sqrt(85))/(18pisqrt(3)) = sum_(n=0)^(infty)((133n+8)(1/2)_n(1/6)_n(5/6)_n)/((n!)^3)(4/(85))^(3n)
(103)
4/pi = sum_(n=0)^(infty)((-1)^n(20n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^32^(2n+1))
(104)
4/(pisqrt(3)) = sum_(n=0)^(infty)((-1)^n(28n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^33^n4^(2n+1))
(105)
4/pi = sum_(n=0)^(infty)((-1)^n(260n+23)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(18)^(2n+1))
(106)
4/(pisqrt(5)) = sum_(n=0)^(infty)((-1)^n(644n+41)(1/2)_n(1/4)_n(3/4)_n)/((n!)^35^n(72)^(2n+1))
(107)
4/pi = sum_(n=0)^(infty)((-1)^n(21460n+1123)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(882)^(2n+1))
(108)
(2sqrt(3))/pi = sum_(n=0)^(infty)((8n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^n)
(109)
1/(2pisqrt(2)) = sum_(n=0)^(infty)((10n+1)(1/2)_n(1/4)_n(3/4)_n)/((n!)^39^(2n+1))
(110)
1/(3pisqrt(3)) = sum_(n=0)^(infty)((40n+3)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(49)^(2n+1))
(111)
2/(pisqrt(11)) = sum_(n=0)^(infty)((280n+19)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(2n+1))
(112)
1/(2pisqrt(2)) = sum_(n=0)^(infty)((26390n+1103)(1/2)_n(1/4)_n(3/4)_n)/((n!)^3(99)^(4n+2)).
(113)

Nämä yhtälöt todistivat ensimmäisen kerran Borwein ja Borwein (1987a, s. 177-187). Borwein ja Borwein (1987b, 1988, 1993) todistivat muita tämäntyyppisiä yhtälöitä, ja Chudnovsky ja Chudnovsky (1987) löysivät samankaltaisia yhtälöitä muille transsendenttisille vakioille (Bailey et al. 2007, s. 44-45).

Täydellinen luettelo tämäntyyppisistä riippumattomista tunnetuista yhtälöistä on

4/pi = sum_(n=0)^(infty)((6n+1)(1/2)_n^3)/(4^n(n!)^3)
(114)
(16)/pi = sum_(n=0)^(infty)((42n+5)(1/2)_n^3)/(64^n(n!)^3)
(115)
(32)/pi = sum_(n=0)^(infty)((42sqrt(5)n+5sqrt(5)+30n-1)(1/2)_n^3)/(64^n(n!)^3)((sqrt(5)-1)/2)^(8n)
(116)
(5^(1/4))/pi = sum_(n=0)^(infty)((540sqrt(5)n-1200n-525+235sqrt(5))(1/2)_n^3(sqrt(5)-2)^(8n))/((n!)^3)
(117)
(12^(1/4))/pi = sum_(n=0)^(infty)((24sqrt(3)n-36n-15+9sqrt(3))(1/2)_n^3(2-sqrt(3))^(4n))/((n!)^3)
(118)

for m=1 nonalternating signs,

2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(12sqrt(2)n-12n-5+4sqrt(2))(sqrt(2)-1)^(4n))/((n!)^3)
(119)
2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(60n-24sqrt(5)n+23-10sqrt(5))(sqrt(5)-2)^(4n))/((n!)^3)
(120)
2/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(420n-168sqrt(6)n+177-72sqrt(6)))/((n!)^3)
(121)
(2sqrt(2))/pi = sum_(n=0)^(infty)((-1)^n(1/2)_n^3(2sqrt(2))^(2n))/((n!)^3)
(122)

for m=1 vuorottelevin merkein,

(128)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(820n^2+180n+13))/(32^(2n)(n!)^5)
(123)
(32)/(pi^2) = sum_(n=0)^(infty)((-1)^n(1/2)_n^5(20n^2+8n+1))/(2^(2n)(n!)^5)
(124)

for m=2 (Guillera 2002, 2003, 2006),

(32)/(pi^3)=sum_(n=0)^infty((1/2)_n^7(168n^3+76n^2+14n+1))/(32^(2n)(n!)^5)
(125)

varten m=3 (Guillera 2002, 2003, 2006), eikä muita m3:lle tunneta (Bailey et al. 2007, s. 45-48).

Bellard antaa eksoottisen kaavan

pi=1/(740025),
(126)

where

P(n)=-885673181n^5+3125347237n^4-2942969225n^3+1031962795n^2-196882274n+10996648.
(127)

Gasper lainaa tuloksen

pi=(16)/3^(-1),
(128)

jossa _1F_2 on yleistetty hypergeometrinen funktio, ja muuntaa sen muotoon

pi=lim_(x-infty)4x_1F_2(1/2;3/2,3/2;-x^2).
(129)

Kiehtova tulos Gosperin ansiosta saadaan

lim_(n-infty)product_(i=n)^(2n)pi/(2tan^(-1)i)=4^(1/pi)=1.554682275.....
(130)

pi täyttää epätasa-arvon

(1+1/pi)^(pi+1) n. 3.14097pi.
(131)

D. Terr (pers. comm.) totesi kummallisen identiteetin

(3,1,4)=(1,5,9)+(2,6,5) (mod 10)
(132)

, joka koskee pii:n yhdeksää ensimmäistä numeroa.

Vastaa

Sähköpostiosoitettasi ei julkaista.