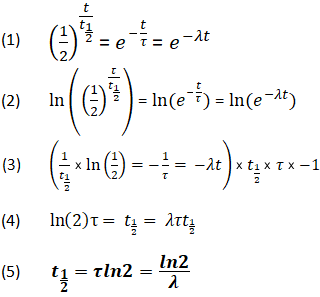Seuraavilla työkaluilla voidaan tuottaa mikä tahansa kolmesta muusta arvosta puoliintumiskaavan puoliintumisajan kaavassa aineelle, jonka hajoaminen vähenee puoleen.

Puoliintumisaikalaskuri
Lisää mikä tahansa kolmesta seuraavassa esitetystä, jotta voit laskea neljännen arvon.
Puoliintumisajan, keskimääräisen eliniän ja hajoamisvakion muuntaminen
Tarjoa jokin seuraavista saadaksesi kaksi muuta arvoa.
Määritelmä ja kaava
Puoliintumisaika määritellään ajaksi, joka kuluu tietyllä suureella pienentyäkseen puoleen alkuperäisestä arvostaan. Termiä käytetään yleisimmin radioaktiivisesti hajoavien atomien yhteydessä, mutta sitä voidaan käyttää kuvaamaan myös muunlaista, eksponentiaalista tai ei eksponentiaalista hajoamista. Yksi tunnetuimmista puoliintumisajan sovelluksista on hiili-14-datointi. Hiili-14:n puoliintumisaika on noin 5 730 vuotta, ja sen avulla voidaan luotettavasti mitata noin 50 000 vuoden takaisia päivämääriä. Hiili-14-datointiprosessin kehitti William Libby, ja se perustuu siihen, että ilmakehässä syntyy jatkuvasti hiili-14:tä. Se kulkeutuu kasveihin fotosynteesin kautta ja sitten eläimiin, kun ne syövät kasveja. Hiili-14 hajoaa radioaktiivisesti, kun kasvi tai eläin kuolee, ja hiili-14:n määrän mittaaminen näytteestä antaa tietoa siitä, milloin kasvi tai eläin kuoli.
Alhaalla on esitetty kolme ekvivalenttia kaavaa, jotka kuvaavat eksponentiaalista hajoamista:
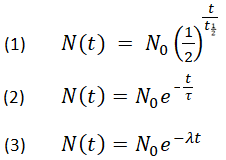
- jossa
N0 on alkuperäinen määrä
Nt on ajan kuluttua jäljellä oleva määrä, t
t1/2 on puoliintumisaika
τ on keskimääräinen elinikä
λ on hajoamisvakio
Jos arkeologi löytäisi fossiilinäytteen, joka sisälsi 25 % hiili-14:ää elävään verrattuna, fossiilisen näytteen kuolinaika voitaisiin määrittää järjestämällä yhtälö 1 uudelleen, koska Nt, N0 ja t1/2 tunnetaan.
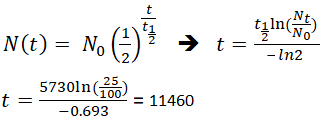
Tämä tarkoittaa, että fossiili on 11 460 vuotta vanha.
Puoliintumisajan vakioiden välisen suhteen derivointi
Ylläolevien yhtälöiden avulla voidaan johtaa suhde myös t1/2:n, τ:n ja λ:n välille. Tämän suhteen avulla voidaan määrittää kaikki arvot, kunhan ainakin yksi niistä tunnetaan.