Rotaatiokinematiikka - Fysiikka 298

”Miehet puhuvat ajan tappamisesta, kun taas aika hiljaa tappaa heidät.”
Dion Boucicault – Lontoon vakuutus (1841)

Tähän mennessä olemme tarkastelleet hiukkasten kinematiikkaa ja dynamiikkaa, mukaan lukien translaatio- ja ympyräliikettä sekä hiukkasjärjestelmien (erityisesti jäykkien kappaleiden) translaatioliikettä systeemin massakeskipisteen liikkeen kannalta. Jälkimmäisessä tapauksessa voimme kuvitella, että kappaleen koko massa sijaitsee massakeskipisteessä ulkoisten translaatiovoimien osalta.

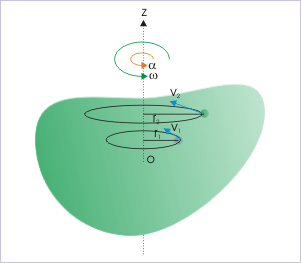Seuraavaksi tarkastellaan jäykän kappaleen pyörimistä kiinteän pyörimisakselin ympäri. Huomaa, että koska tarkastelemme jäykkää kappaletta, jokainen kappaleen hiukkanen pysyy kiinteänä suhteessa muihin. Tämä tarkoittaa, että tällaisessa pyörimisliikkeessä jokainen hiukkanen liikkuu ympyrällä, jonka keskipiste on pyörimisakselilla. Oikealla olevassa kuvassa kappale pyörii z-akselin ympäri; kaksi näytehiukkasta liikkuvat ympyröissä, joiden säteet ovat r1 ja r2. Jos voimme kuvata hiukkasen ympyräliikettä ilman suoraa viittausta sen säteeseen, kaikki systeemin hiukkaset kuvataan samoilla yhtälöillä. Vaikka hiukkasten säteet ovat erilaiset, niiden kulmakierrot ovat samat. Siksi on tarpeen ottaa käyttöön kulmamuuttujat.

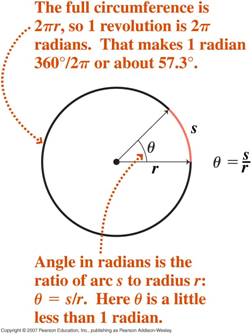
Kulmien radiaani mitta

Kulmanopeus (nopeus) ja kulmakiihtyvyys

Kulmanopeus ja kulmakiihtyvyys määritellään samalla tavalla kuin nopeus ja kiihtyvyys. Kummallekin on olemassa keskiarvot ja hetkelliset arvot.

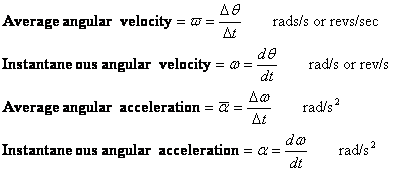
Kulmakiihtyvyys ei ole sama kuin keskipakokiihtyvyys. Keskipakokiihtyvyys johtuu nopeuden suunnan muutoksesta, kulmakiihtyvyys johtuu nopeuden suuruuden muutoksesta (kiertokulman kautta).

Aivan kuten translaatiotapauksessa, kulmanopeuden ja kulmanopeuden ero on suunta. Kulmanopeuteen on sisällyttävä pyörimissuunta kyseisen akselin ympäri. Esimerkiksi 10 rad/s myötäpäivään x-akselin ympäri on kulmanopeus, 10 rad/s x-akselin ympäri on kulmanopeus.

Kiertokinemaattiset yhtälöt

Suorassa analogiassa translaatiokinemaattisten yhtälöiden kanssa ympyräliike yhden akselin ympäri vakiokulmakiihtyvyydessä voidaan kuvata seuraavilla neljällä yhtälöllä,

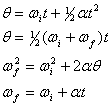
jossa olemme tehneet korvaukset,

Huomaa, että aivan kuten +x määritellään mielivaltaisesti oikealle, myös thetan positiivinen arvo voidaan määritellä myötä- tai vastapäivään.

Kulma- ja translaatiomuuttujien välinen suhde

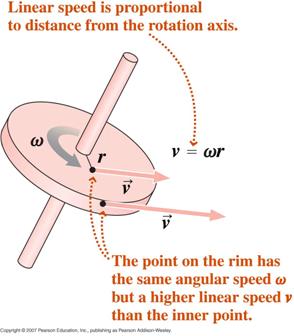Lähdetään liikkeelle radiaani-mitan määritelmästä differentioimalla ajan suhteen ja osoitetaan, että,

missä v on tangentiaalinen nopeus ja a on tangentiaalinen kiihtyvyys.

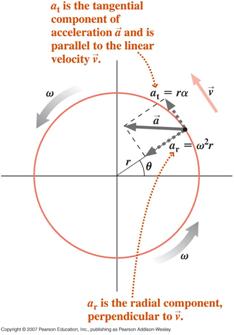
Ympyräliikettä suorittava hiukkanen, jonka kulmanopeus vaihtelee (epäyhtenäinen ympyräliike), kokee kaksi kiihtyvyyskomponenttia, tangentiaalisen komponentin, joka johtuu sen nopeuden muuttuvasta suuruudesta, ja radiaalisen (sentripetaalisen) komponentin, joka johtuu sen nopeuden muuttuvasta suunnasta

Hiukkasen nettokiihtyvyys on näiden kahdesta komponenteista muodostuva vektorisumma, kuten alla on esitetty.

Tiedoksi…

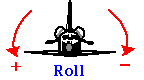
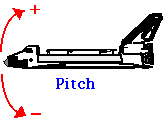
Samanaikaista pyörimistä useamman kuin yhden akselin ympärillä voidaan tarkastella vastaavalla tavalla kuin ammuksen liikettä, jossa laajensimme 1D-translaatiokeskustelumme 2D-liikkeeseen. Ilmailusovelluksissa kolmen akselin ympäri tapahtuvaa pyörimistä kuvataan nimillä Roll, Pitch ja Yaw.