
Neuraaliset verkot ja matematiikka ovat erottamattomia, ja se luultavasti pelottaa useimpia ihmisiä. Olen kuullut liian monta epäilevää kommenttia Deep Learningista: ”Voi, tässä on liikaa matematiikkaa, jota en pysty ymmärtämään”, ”Kuinka moni yritys käyttää Deep Learningia oikeasti? Säästän mieluummin itseni aivojumpalta ja pysyn kaukana näistä vaativista käsitteistä.”
Mutta jos ajattelet asiaa, se ei ole niin vaikeaa. Luota minuun! Ymmärtääksesi, miksi algoritmi käyttäytyy tietyllä tavalla, on tärkeää ymmärtää, mitä kulissien takana tapahtuu. Monimutkaiset koneoppimisalgoritmit on nykyään pakattu meille kätevästi ja ne ovat vain funktiokutsun päässä. Aktivointifunktioiden johdannaiset ovat hieman vähemmän ilmeisiä käsitteitä, jotka meillä on usein tapana jättää huomiotta. Ne muodostavat kuitenkin tehokkaiden algoritmien perustan, ja pienen lisäpanostuksen panostaminen niiden ymmärtämiseen kannattaa varmasti. Tämän artikkelin luettuasi olet askeleen lähempänä sen selvittämistä, mitä ”mustan laatikon” julkisivun alla piilee.
Tausta
Neuraaliset verkot käyttävät piilo- ja ulostulokerroksissa erilaisia aktivointifunktioita oppimisprosessin katalysoimiseksi. Muutamia yleisesti käytettyjä aktivointifunktioita ovat Sigmoid- ja tanH-funktiot. Suosituin aktivointifunktio on ReLU ( Rectified Linear Unit), koska se pystyy tehokkaasti voittamaan häviävän gradientin ongelman. Aktivointifunktioiden syvällinen tarkastelu on toista päivää varten. Tänään keskitymme Sigmoid-funktion derivaatan taustalla olevaan matematiikkaan.
Miksi aktivointifunktion derivaatta on tärkeä?
Kuten varmaan tiedätkin, neuroverkkoja ohjaa kaksi vaihetta:
- Forward Propagation – Syöttötiedot kulkevat verkon läpi ja saamme ennustetun ulostulon. Vertaamme sitä todelliseen ulostuloon ja laskemme virheen.
- Takaisinlevitys – Laskettua virhettä käytetään neuroverkon parametrien päivittämiseen aktivointifunktion derivaatan avulla.
Sigmoidifunktio
Sigmoidifunktiota, jolle on ominaista S-muotoinen käyrä, kutsutaan usein logistisen funktion erikoistapaukseksi. Se on käyttökelpoisin tapauksissa, joissa on ennustettava todennäköisyyttä tulosteena.
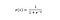
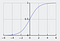
Sigmoidifunktio tuottaa arvoja, jotka ovat 0:n ja 1:n väliltä (oikeutetusti ottaen huomioon, että se ennustaa todennäköisyyksiä).
Sigmoidijohdannainen
Tämä perustavanlaatuinen rakennuspalikka, jonka avulla voidaan kouluttaa neuroverkkoja, on seuraavanlainen:


Pidemmittä puheitta, aloitetaan derivointi!
Lähestymistapa 1

Lähestymistapa 2:
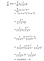
Miksi käytämme tätä versiota johdannaisesta?
Eteenpäin etenemisvaiheessa lasketaan sigmoidifunktio (σ(x)) ja sen arvo on käsillä. Kun lasket derivaatan takaisinkulkeutumisvaiheessa, sinun tarvitsee vain liittää σ(x):n arvo edellä johdettuun kaavaan ja voila, olet valmis!
Tässä se on, kaverit! Kiitos lukemisesta!