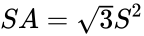Tetrahedron

Akatemiallehdestä katso Tetrahedron (lehti).

Säännöllinen tetraedri
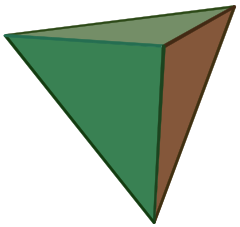(Klikkaa tästä pyörivään malliin)
Tyyppi	Platoninen kiinteä kappale
Elementit	F = 4, E = 6 V = 4 (χ = 2)
Pinnat sivujen mukaan	4{3}
Schläfli symboli	{3,3} ja s{2,2}
Wythoff-symboli	3 \| 2 3 \| 2 2 2
Coxeter-Dynkin
Symmetria	Td tai (*332)
	U01, C15, W1
Ominaisuudet	Säännöllinen kupera deltaedri
Dihedrikulma	70.528779° = arccos(1/3)
3.3. Säännöllinen tetraedri on sellainen tetraedri, jonka neljä kolmiota ovat säännöllisiä eli ”tasasivuisia”, ja se on yksi platonisista kappaleista. Tetraedri on eräs pyramidin laji, joka on polyedri, jolla on litteä monikulmion pohja ja kolmionmuotoiset sivut, jotka yhdistävät pohjan yhteiseen pisteeseen. Tetraedrin tapauksessa pohja on kolmio (mitä tahansa neljästä pinnasta voidaan pitää pohjana), joten tetraedri tunnetaan myös nimellä kolmiopyramidi tai digonaalinen deltaedri. Säännöllisen tetraedrin kaavat Tilavuus on $V={\frac {\sqrt {3}}{12}}S^{3}}$ Pinta-ala on $SA={\sqrt {3}}S^{2}$ Template:Commonscat F. M. Jackson ja Weisstein, Eric W., ”Tetrahedron” osoitteesta MathWorld. Interactive Polyhedron Model K. J. M. MacLean, A Geometric Analysis of the Five Platonic Solids and Other Semi-Regular Polyhedra Piero della Francescan kaava tetraedrin tilavuudelle osoitteessa MathPages Vapaat paperimallit tetraedristä ja monista muista polyedereistä An Amazing, Space Filling, Non-regular Tetrahedron, joka sisältää myös kuvauksen ”rotating ring of tetrahedra”, joka tunnetaan myös nimellä kaleidocycle. Tetraedrin ydinverkko Tetraedrin rakenteen soveltaminen joustavan osittaisverkon tietoverkon luomiseen Explisiittiset tarkat kaavat mielivaltaisen tetraedrin inertia tensorille sen kärkikoordinaattien suhteen Tetraedrin inertia tensorille

Säännöllisen tetraedrin kaavat

Vastaa Peruuta vastaus