Le courant alternatif, ou courant alternatif, est ainsi nommé parce que le courant alterne ou bascule entre deux polarités. En d’autres termes, le courant (et par conséquent la tension) est une fonction du temps. Ce phénomène est fondamentalement différent du courant continu, dont la polarité est fixe et généralement constante dans le temps. Une source de tension continue de laboratoire, par exemple, maintient idéalement une tension fixe à ses bornes et ne varie pas dans le temps. En revanche, lorsqu’une forme d’onde alternative oscille d’avant en arrière dans le temps, sa forme peut présenter de grandes variations allant des trajectoires simples et régulières des normes de laboratoire telles que les ondes sinusoïdales, les ondes triangulaires et les ondes carrées, aux formes d’onde beaucoup plus complexes et ondulantes produites par les instruments de musique et la voix humaine.
L’onde sinusoïdale est l’onde la plus simple qui puisse être créée. Elle représente le mouvement d’un vecteur simple tournant à une vitesse constante, comme le déplacement vertical de la trotteuse d’une horloge. Un exemple est illustré sur la figure \(\PageIndex{1}\). L’axe horizontal représente le temps. Il augmente au fur et à mesure que l’on se déplace de gauche à droite (c’est-à-dire que si le point A est à droite du point B, alors A se produit plus tard dans le temps que B). L’axe vertical est représenté ici en général comme un pourcentage du maximum, mais il s’agirait ordinairement d’une mesure de tension, de courant, de pression acoustique ou autre.
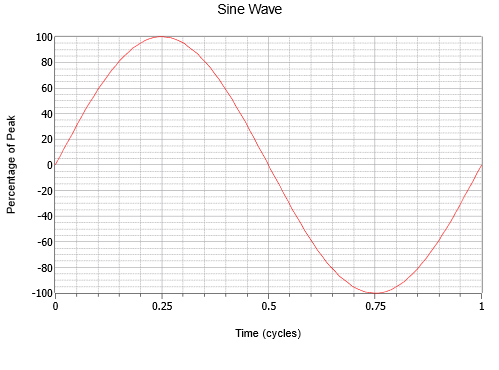
Figure \(\PageIndex{1}\) : Une onde sinusoïdale.
Notez la variation régulière qui commence à zéro, s’élève jusqu’à un pic positif au quart du parcours, retombe à zéro à la moitié du parcours, continue jusqu’à un pic négatif aux trois quarts du parcours, puis remonte à nouveau au point de départ. Ce processus se répète ensuite. Chaque répétition est appelée un cycle. La figure \(\PageIndex{1}\) montre un cycle complet.
Les ondes sinusoïdales présentent une symétrie en quart d’onde. C’est-à-dire que chaque quart (dans le temps) de l’onde est identique à n’importe quel autre si vous le retournez simplement autour de l’axe horizontal et/ou si vous le faites tourner à la verticale autour de son sommet. Le temps nécessaire pour accomplir un cycle est appelé période et est désigné par le symbole \(T\) (pour Time). L’inverse de la période est la fréquence, \(f\).
\
La fréquence indique combien de cycles existent en une seconde. Pour rendre hommage à l’un des chercheurs du 19ème siècle dans ce domaine, au lieu d’appeler l’unité « cycles par seconde », nous utilisons le terme Hertz, du nom de Heinrich Hertz et abrégé en Hz. Sur la figure \(\PageIndex{2}\), trois ondes sinusoïdales sont représentées avec des fréquences différentes ; l’onde initiale (verte), une onde à deux fois la fréquence (bleue), et une troisième à la moitié de la fréquence ou à deux fois la période (rouge).
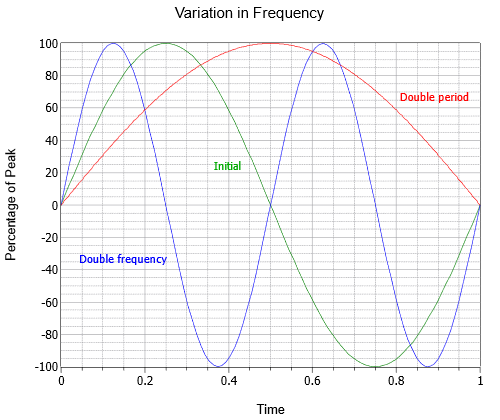
Figure \(\PageIndex{2}\) : Variation de la fréquence de l’onde sinusoïdale.
L’amplitude (verticale) de l’onde peut être exprimée comme une quantité de crête, qui est le changement de la ligne zéro centrale jusqu’à la valeur la plus positive. L’amplitude peut également être exprimée comme pic à pic ; la distance entre la valeur la plus négative et la valeur la plus positive. Pour une onde sinusoïdale, cette valeur sera toujours égale au double de la valeur de crête, bien que cela puisse ne pas être le cas pour d’autres ondes qui peuvent être asymétriques. La figure \(\PageIndex{3}\) présente une série de trois ondes sinusoïdales d’amplitudes différentes. À côté de l’initiale (verte) se trouvent des versions à double amplitude (bleue) et à demi-amplitude (rouge).
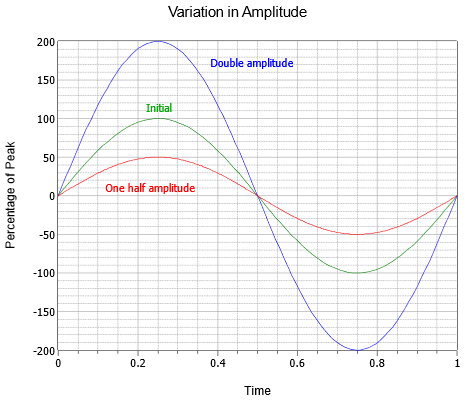
Figure \(\PageIndex{3}\) : Variation de l’amplitude de l’onde sinusoïdale.
En combinant ces paramètres, considérez la forme d’onde de tension représentée sur la figure \(\PageIndex{4}\). Nous voyons ici deux cycles d’une forme d’onde de tension alternative.
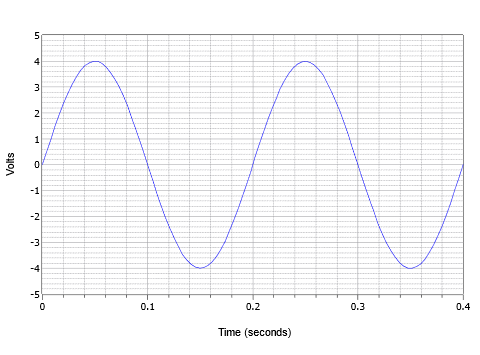
Figure \(\PageIndex{4}\) : Exemple d’onde sinusoïdale de base.
La valeur de crête est de 4 volts et la valeur crête à crête est de 8 volts (généralement abrégée en « 8 V pp »). La période d’un cycle est de 0,2 seconde, soit \(T = 200\) millisecondes. En outre, la fréquence, \(f = 1/200\) millisecondes, ou 5 Hz (5 cycles en une seconde).
Les formes d’onde CA peuvent également être combinées avec un décalage CC. L’ajout d’un niveau de courant continu positif décale l’onde verticalement vers le haut, tandis qu’un niveau de courant continu négatif décale l’onde verticalement vers le bas. Cela ne modifie pas la fréquence ou la partie AC de l’amplitude (bien que les pics absolus soient décalés de la valeur DC). La figure \(\PageIndex{5}\) montre l’effet de divers décalages de CC. Au-dessus de l’onde initiale (vert) se trouve une onde identique avec un décalage CC positif égal à 20 % de la valeur de crête originale (bleu). Sous l’original se trouve une troisième onde (rouge) qui présente un décalage CC négatif égal à la moitié de la valeur de crête de l’original.
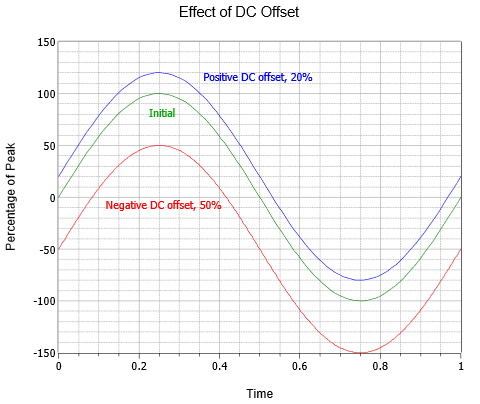
Figure \(\PageIndex{5}\) : Variation du décalage en courant continu d’une onde sinusoïdale.
De plus, il est possible qu’une onde sinusoïdale soit décalée dans le temps par rapport à une autre onde sinusoïdale ou à une référence. Bien qu’il soit possible d’indiquer ce décalage sous la forme d’un temps absolu, il est plus courant de le faire sous la forme d’un décalage de phase, c’est-à-dire le temps exprimé comme une portion de la période en degrés. Par exemple, si un sinus est en avance sur un autre d’un quart de la période, on dit qu’il est en avance de 90\(^{\circ}\) (c’est-à-dire 1/4 de 360\(^{\circ}\)). S’il est en retard de ½ de la période, on dit qu’il est en retard de 180\(^{\circ}\) (c’est-à-dire en retard d’un demi-cycle). Une autre façon de le dire est que les formes d’onde en avance commencent plus tôt dans le temps et sont donc dessinées à gauche de la référence, tandis que les formes d’onde en retard commencent plus tard dans le temps et sont dessinées à droite.
La figure \(\PageIndex{6}\) illustre l’effet du déphasage. Notez que dans ce tracé, \(t = 0\) a été déplacé au centre de l’axe horizontal. La courbe du milieu est l’onde initiale, ou de référence, (verte). À gauche (rouge), on trouve une onde qui précède l’onde initiale d’un huitième de cycle, soit 45\(^{\circ}\). À droite (bleu), on trouve une onde en retard de moitié moins, soit -22,5\(^{\circ}\).
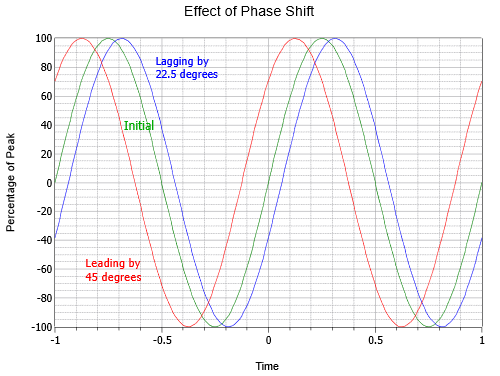
Figure \(\PageIndex{6}\) : Variation de la phase de l’onde sinusoïdale.
La combinaison des éléments précédents nous permet de développer un format général pour une onde sinusoïdale (tension représentée) :
\
Où
\(v(t)\) est la tension à un certain temps \(t\),
\(V_{DC}\) est le décalage DC, s’il y en a un,
\(V_{P}\) est la valeur de crête,
\(f\) est la fréquence,
\(\theta\) est le déphasage (+ si en avance et dessiné vers la gauche, – si en retard et dessiné vers la droite).
Pour un exemple rapide et pratique, la forme d’onde représentée sur la figure \(\PageIndex{4}\) a une amplitude de 4 volts crête, une fréquence de 5 Hz, et aucun décalage en courant continu ou déphasage. Son expression est donc : \(v(t) = 4 \sin (2 \pi 5 t)\)
Pour calculer un déphasage, déterminez d’abord le différentiel de temps entre la forme d’onde et la référence, que nous appellerons \(\Delta t\). La référence peut être un point fixe dans le temps (par exemple, \(t = 0\)) ou une autre forme d’onde. En général, la façon la plus simple de procéder est de mesurer la différence aux passages à zéro, en supposant qu’il n’y a pas de décalage DC. S’il y a un décalage, effectuez la mesure à l’endroit où le passage à zéro a été déplacé (c’est-à-dire au niveau du décalage CC). Une fois la différence trouvée, divisez-la par la période pour représenter le décalage comme une fraction de période. Comme un cycle représente une rotation du vecteur, soit 360 degrés, il suffit de multiplier la fraction par 360 degrés pour trouver le déphasage en degrés. Exprimé sous la forme d’une formule :
\
Rappellez-vous, si l’onde est décalée vers la gauche, alors elle est en avance et positive, tandis qu’un décalage vers la droite est en retard ou retardé dans le temps, et donc négatif.
Exemple \(\PageIndex{1}\)
Écrivez l’expression de la forme d’onde représentée sur la figure \(\PageIndex{7}\).
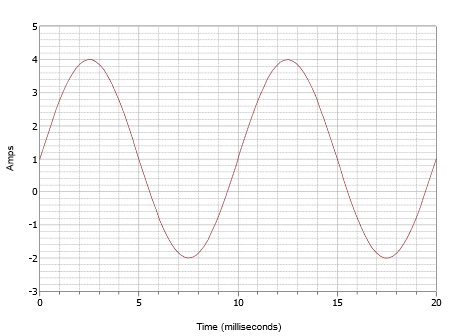
Figure \(\PageIndex{7}\) : Forme d’onde pour l’exemple \(\PageIndex{1}\).
Cette forme d’onde peut superficiellement ressembler à celle de la figure \(\PageIndex{4}\) mais ne vous laissez pas tromper. Tout d’abord, l’échelle de temps est différente. Pour cette forme d’onde, un cycle se termine en 10 millisecondes. Par conséquent, la fréquence est
\
\
\
Le deuxième problème est le décalage DC. Notez que le pic positif se produit à 4 ampères tandis que le pic négatif se produit à -2 ampères. Cela indique une valeur de crête à crête de 6 ampères. Sans décalage, le pic positif serait à 3 ampères, il y a donc un décalage CC de +1 ampère. Le centre vertical de la forme d’onde est décalé vers le haut de 0 ampère à +1 ampère. Ce point est à t = 0, par conséquent, il n’y a pas de déphasage. L’expression résultante est :
\
Exemple \(\PageIndex{2}\)
Ecrire l’expression pour la forme d’onde montrée dans la Figure \(\PageIndex{8}\).
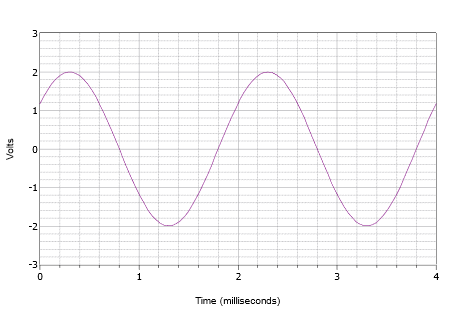
Figure \(\PageIndex{8}\) : Forme d’onde pour l’exemple \(\PageIndex{2}\).
Tout d’abord, la crête positive est de 2 volts et la valeur crête à crête est de 4 volts. Il n’y a donc pas de décalage en courant continu. Le centre vertical de l’onde ne commence pas à \(t = 0\), il doit donc y avoir un déphasage. La valeur à \(t = 0\) est de 1,2 volts. L’onde atteint cette même amplitude à \(t = 2\) millisecondes et commence à répéter un autre cycle. Par conséquent, la période doit être de 2 millisecondes. La fréquence est l’inverse de cette valeur, et donc \(f = 500\) Hz.
La forme d’onde est décalée vers la gauche, ce qui indique un déphasage positif ou avant. Si nous examinons le deuxième cycle, nous voyons qu’il atteint zéro volt à 1,8 millisecondes. Par conséquent, le décalage est de 0,2 millisecondes. Exprimé en degrés, cela donne :
\
\
\
L’expression finale est :
\
Exemple \(\PageIndex{3}\)
Dessinez la forme d’onde correspondant à l’expression suivante.
\
Premièrement, notez que le décalage de -3 volts pousse le pic positif vers le bas de 5 volts à 2 volts, et le pic négatif vers le bas de -5 volts à -8 volts. La fréquence de 40 kHz impose une période de :
\
\
\
Le déphasage de -72\(^{\circ}\) représente 72/360, soit 0,2 cycle. Cela correspond à un retard (décalé vers la droite car il est négatif) de 0,2 fois 25 \(\mu\)s, soit 5 \(\mu\)s.
Initialement, il est souvent préférable de construire le tracé via une série d’étapes discrètes plutôt que d’essayer de le dessiner entièrement en une seule fois. Tout d’abord, dessinez une onde sinusoïdale avec une amplitude de crête de 5 volts et une période de 25 \(\mu\)s. Maintenant, poussez la forme d’onde vers le bas de 3 volts afin que le pic positif ne soit plus que de 2 volts et que le pic négatif soit à -8 volts. Enfin, poussez la nouvelle forme d’onde décalée vers la droite de 5 \(\mu\)s. Le résultat est illustré sur la Figure \(\PageIndex{9}\).
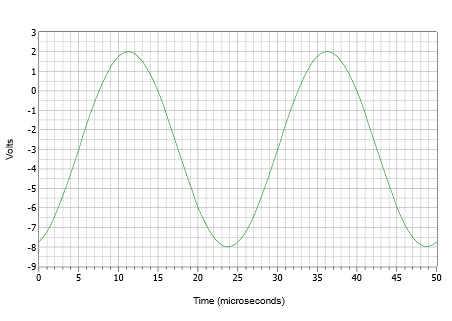
Figure \(\PageIndex{9}\) : Forme d’onde pour l’exemple \(\PageIndex{3}\).
1.2.1 : Mesures en laboratoire
En laboratoire, on utilise un générateur de fonctions pour générer des sinus et autres formes d’ondes. Ces appareils permettent un contrôle précis de l’amplitude et de la fréquence de l’onde, ainsi que l’ajout d’un décalage en courant continu, si nécessaire. Un exemple est illustré sur la figure \(\PageIndex{10}\). L’outil de mesure correspondant est l’oscilloscope, ou simplement scope, pour faire court.

Figure \(\PageIndex{10}\) : Générateur de signaux de laboratoire.
L’oscilloscope est peut-être le dispositif de mesure le plus utile et le plus polyvalent du laboratoire. Généralement, ils comportent deux ou quatre canaux d’entrée, bien que davantage soient possibles. Chaque voie d’entrée dispose de son propre réglage de sensibilité et toutes les voies partagent une référence temporelle commune. L’écran affiche les formes d’onde de la même manière que celles présentées dans les figures \(\PageIndex{1}\) – \(\PageIndex{9}\). Ils peuvent également tracer une tension en fonction d’une autre (mode X – Y). Les oscilloscopes modernes disposent de fonctionnalités supplémentaires telles que la mesure automatique de la fréquence, de l’amplitude, du déphasage, etc., les mesures basées sur le curseur et la possibilité d’enregistrer les images affichées sous forme de fichiers graphiques. Un exemple d’oscilloscope numérique à quatre canaux est illustré à la figure \(\PageIndex{11}\).

Figure \(\PageIndex{11}\) : Un oscilloscope numérique.
1.2.2 : Symboles des schémas
En ce qui concerne les schémas, les symboles des sources de tension et de courant alternatif sont représentés sur la figure \(\PageIndex{12}\). Les repères de polarité et de direction ne sont pas absolus ; après tout, il s’agit de sources de courant alternatif dont la polarité et la direction changent dans les deux sens. Les marqueurs sont plutôt utilisés pour établir une référence temporelle, en particulier dans les circuits utilisant des sources multiples.
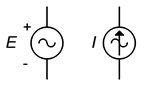
Figure \(\PageIndex{12}\) : Symboles schématiques d’une source de tension alternative (à gauche) et d’une source de courant (à droite).
Il est bon de rappeler que la négation d’une source revient à inverser sa polarité. Ceci était vrai pour les sources de courant continu et reste vrai pour les sources de courant alternatif. Ceci est illustré sur la figure \(\PageIndex{13}\). Parfois, l’inversion ou la négation de la source rend l’analyse un peu plus évidente ou plus facile à visualiser.
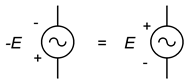
Figure \(\PageIndex{13}\) : Équivalence de polarité/signe.
Exemple \(\PageIndex{4}\)
Supposons qu’un oscilloscope affiche deux ondes telles que représentées sur la figure \(\PageIndex{14}\). Déterminez le déphasage de la plus petite forme d’onde de 20 volts crête (bleu) par rapport à la plus grande forme d’onde de 25 volts crête (rouge).
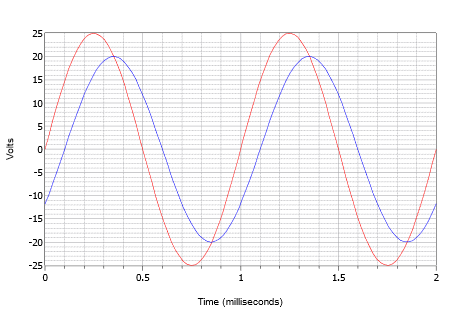
Figure \(\PageIndex{14}\) : Formes d’onde de l’exemple \(\PageIndex{4}\).
Premièrement, notez qu’aucune des deux ondes ne présente un décalage en courant continu. Si l’une ou les deux présentaient un décalage, il faudrait décaler verticalement la ou les ondes pour que leurs points normaux de passage à zéro soient au même niveau. En mesurant l’une ou l’autre des ondes, on constate que la période est de 1 milliseconde. Le décalage temporel le plus facile à trouver est celui de l’un des passages à zéro (il y a quatre emplacements au choix). Le retard est d’un petit écart, soit 0,1 milliseconde, la plus petite onde étant retardée dans le temps, ou en retard sur la plus grande onde. Cela indique un déphasage négatif.
\
\
\
1.2.3 : Sinus et Cosinus
Il existe une poignée de déphasages spécifiques qui méritent d’être examinés de plus près. Si une onde sinusoïdale est inversée, c’est-à-dire retournée à l’envers, il est impossible de la distinguer d’une onde sinusoïdale qui a été décalée de +180 ou -180 degrés. En d’autres termes, une telle onde peut être écrite de trois manières différentes : \(- \sin (2 \pi ft)\), \(\sin (2 \pi ft – 180^{\circ})\), ou \(\sin (2 \pi ft + 180^{\circ})\). De plus, si une onde sinusoïdale est décalée de +90 degrés (c’est-à-dire vers l’avant et vers la gauche), elle peut également être qualifiée d’onde cosinusoïdale. Ainsi, \(\sin (2 \pi ft + 90^{\circ}) = \ cos (2 \pi ft)\). Enfin, si une onde sinusoïdale est décalée de -90 degrés (c’est-à-dire en retard et vers la droite), on peut parler d’une onde cosinusoïdale négative ou inversée. Ainsi, \(\sin (2 \pi ft – 90^{\circ}) = – \cos (2 \pi ft)\). Les relations de ces quatre ondes sont illustrées sur la figure \(\PageIndex{15}\).
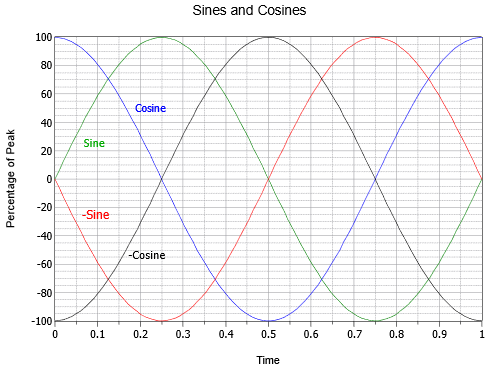
Figure \(\PageIndex{15}\) : Relations temporelles entre les sinus et les cosinus.
Il convient également de noter que l’onde cosinus représente la première dérivée, ou pente, de l’onde sinus. Comme vous vous en souvenez peut-être dans d’autres études, la pente ou la « raideur » d’une ligne est le rapport entre le changement vertical et le changement horizontal, parfois appelé « la montée sur la descente ». Pour une tension, il s’agit de la variation de la tension par rapport à la variation du temps, ou \(\Delta V/ \Delta t\). Pour une courbe lisse à variation continue comme une onde sinusoïdale, la pente à un point donné est définie correctement comme la dérivée première, ou \(dv/dt\) dans ce cas. Pour vérifier visuellement que cela est vrai, notez que la partie la plus raide de l’onde sinusoïdale (en vert) se trouve à l’endroit où elle passe par l’amplitude zéro. Lorsqu’elle passe par zéro en se déplaçant positivement (à \(t = 0\) ou \(t = 1\) dans la figure \(\PageIndex{15}\)), le cosinus (bleu) est à son pic positif. Lorsque le sinus passe par zéro en se déplaçant vers le négatif (à \(t = 0,5\)), le cosinus est à son pic négatif. De plus, l’onde sinusoïdale est plate avec une pente de zéro à ses pics positif et négatif (à \(t = 0,25\) et \(t = 0,75\), respectivement), et à ces moments-là, l’amplitude du cosinus est également nulle. Il est également vrai que l’onde sinus est la pente de l’onde cosinus négative, que le cosinus négatif est la pente du sinus négatif et que le sinus négatif est la pente du cosinus. Dans le sens inverse, nous pouvons dire que l’anti-dérivée (intégrale indéfinie) d’une onde cosinusoïdale est une onde sinusoïdale, que l’intégrale d’une onde sinusoïdale est une onde cosinusoïdale négative, et ainsi de suite. Ces relations se révéleront des plus utiles lorsque nous porterons notre attention sur la réponse des condensateurs et des inductances dans les circuits alternatifs.
1.2.4 : RMS – Mesure de la moyenne quadratique
A l’instar de la crête et de la crête à crête, l’amplitude peut être donnée sous forme de valeur RMS (Root Mean Square). En fait, si la valeur crête ou crête à crête n’est pas spécifiée, la mesure est supposée être RMS. La valeur efficace est un calcul spécial utilisé pour trouver la puissance équivalente en courant continu (très courant, par exemple, avec les amplificateurs de puissance audio). En d’autres termes, si l’on souhaite déterminer la puissance d’une résistance, le calcul doit être effectué en utilisant les valeurs RMS de la tension ou du courant, et non les valeurs crêtes ou crête à crête. Si l’on ne procède pas ainsi, on obtiendra des puissances erronées. Ceci est vrai quelle que soit la forme d’onde, qu’il s’agisse d’une onde sinusoïdale, d’une onde triangulaire ou des ondes complexes des signaux musicaux. Si une tension est spécifiée comme RMS, elle peut être traitée pour les calculs de puissance comme une tension continue de taille équivalente. Par exemple, une tension sinusoïdale RMS de 1 volt produira la même dissipation de puissance et le même échauffement dans une résistance donnée qu’une tension continue de 1 volt. Pour cette raison, RMS est parfois appelé la valeur effective (c’est-à-dire la valeur DC effective).
Le nom racine carrée moyenne décrit le processus de détermination de la valeur effective. Tout d’abord, rappelons que la puissance est proportionnelle au carré de la tension ou du courant. Ainsi, notre première étape sera de mettre au carré la forme d’onde d’entrée. Bien sûr, la forme d’onde est une fonction du temps et son carré donnera une nouvelle forme. À ce stade, nous devons trouver la valeur moyenne de cette nouvelle forme. La raison en est simple, mais pas forcément évidente. Les composants électriques et électroniques ont une masse, et ne chauffent ou ne refroidissent donc pas instantanément. Ils présentent une constante de temps thermique. Par conséquent, ils répondent à l’entrée moyenne dans le temps. Bien que nous puissions calculer une sorte de « puissance de crête instantanée » à un moment précis dans le temps, cela ne représente pas la puissance CC équivalente. Une fois que nous avons obtenu la valeur moyenne de cette forme d’onde au carré, la valeur CC correspondante est simplement la racine carrée de la moyenne. Le résultat est une valeur fractionnaire entre zéro et un qui est utilisée comme facteur d’échelle pour transformer une valeur de crête en une valeur RMS. La valeur sera unique pour la forme d’onde spécifique. Ainsi, toutes les sinusoïdes (quelle que soit leur phase) ont le même facteur, toutes les ondes triangulaires régulières ont le même facteur, et ainsi de suite. Comme nous nous préoccupons principalement des sinus, examinons de plus près la détermination du facteur efficace pour eux.
Nous commençons par l’expression de base pour une onde sinusoïdale sans décalage DC ou déphasage, et avec une amplitude de un :
La première étape consiste à élever au carré cette forme d’onde. Une identité trigonométrique utile est
\
L’application à notre onde donne :
\
Cette expression décrit une onde cosinusoïdale inversée à deux fois la fréquence d’origine et à la moitié de l’amplitude d’origine, chevauchant un décalage DC égal à sa valeur de crête. En d’autres termes, le pic négatif du cosinus est à zéro et le pic positif est à 1. L’étape suivante consiste à trouver la valeur moyenne ou moyenne de ce résultat intermédiaire. La moyenne est égale au décalage de 0,5. Cela peut être visualisé comme la zone au-dessus du décalage remplissant parfaitement le « creux » sous le décalage. L’étape finale consiste à prendre la racine carrée de la moyenne. La racine carrée de 0,5 est égale à une fois la racine carrée de deux, soit environ 0,707. Par conséquent, la valeur RMS est égale à 0,707 fois la crête. Vous pouvez également diviser le pic par la racine carrée de deux, soit environ 1,414. Ce processus est illustré graphiquement dans la figure \(\PageIndex{16}\).
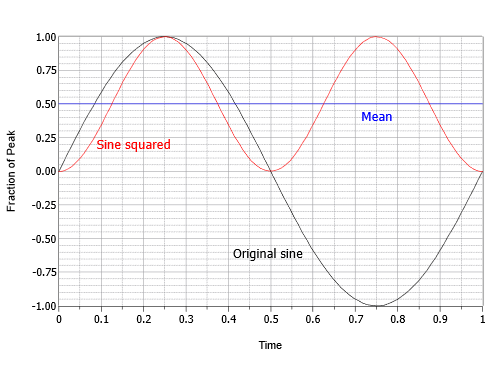
Figure \(\PageIndex{16}\) : Processus pour trouver le facteur RMS pour les sinus.
En résumé, pour les ondes sinusoïdales, RMS est toujours la valeur de crête fois 0,707. Nous pourrions également dire que la valeur efficace de toute onde sinusoïdale est sa crête divisée par environ 1,414. Là encore, ces rapports ne sont pas nécessairement vrais pour les ondes non sinusoïdales. Vous trouverez des détails concernant d’autres formes courantes à l’annexe C. Enfin, le rapport entre la valeur de crête et la valeur efficace est appelé le rapport de crête. Il s’agit d’une valeur fixe pour les ondes sinusoïdales (encore une fois, environ 1,414), mais elle peut dépasser 10:1 pour certains types de signaux audio.
1.2.5 : Longueur d’onde
Un autre élément d’intérêt est la vitesse de propagation de l’onde. Celle-ci varie considérablement. Dans le cas de la lumière dans le vide (ou, pour s’en approcher, d’un courant électrique dans un fil), la vitesse est d’environ 3E8 mètres par seconde (soit 300 000 km/s) ou environ 186 000 miles par seconde.
Donné une vitesse et une période, on peut imaginer à quelle distance se trouvent les pics de l’onde. Cette distance est appelée la longueur d’onde et est désignée par la lettre grecque lambda \(\lambda\). La longueur d’onde est égale à la vitesse divisée par la fréquence, \(\lambda = v/f\). Ainsi, pour un haut-parleur produisant un sinus de 100 Hz, la vitesse du son dans l’air étant de 344 m/s, alors \(\lambda = 344 m/s \, / \, 100\) Hz, soit 3,44 mètres (un peu plus de 11 pieds). Remarquez que plus la fréquence est élevée, plus la longueur d’onde est courte. Notez également que plus la vitesse est élevée, plus la longueur d’onde est grande. Les calculs de longueur d’onde sont particulièrement importants dans les domaines des télécommunications et de l’acoustique.