Résistance des liaisons : Les liaisons covalentes
Les molécules stables existent parce que les liaisons covalentes maintiennent les atomes ensemble. On mesure la force d’une liaison covalente par l’énergie nécessaire pour la rompre, c’est-à-dire l’énergie nécessaire pour séparer les atomes liés. La séparation de toute paire d’atomes liés nécessite de l’énergie ; plus une liaison est forte, plus l’énergie nécessaire pour la rompre est importante. L’énergie nécessaire à la rupture d’une liaison covalente spécifique dans une mole de molécules gazeuses est appelée énergie de liaison ou énergie de dissociation de la liaison. L’énergie de liaison pour une molécule diatomique, \(D_{X-Y}\), est définie comme le changement d’enthalpie standard pour la réaction endothermique :
Par exemple, l’énergie de liaison de la liaison H-H covalente pure, \(\Delta_{H-H}\), est de 436 kJ par mole de liaisons H-H rompues :
Rompre une liaison nécessite toujours d’ajouter de l’énergie à la molécule. Corrélativement, faire une liaison libère toujours de l’énergie.
Les molécules avec trois atomes ou plus ont deux liaisons ou plus. La somme de toutes les énergies de liaison dans une telle molécule est égale à la variation d’enthalpie standard pour la réaction endothermique qui rompt toutes les liaisons de la molécule. Par exemple, la somme des quatre énergies de liaison C-H dans CH4, 1660 kJ, est égale au changement d’enthalpie standard de la réaction:
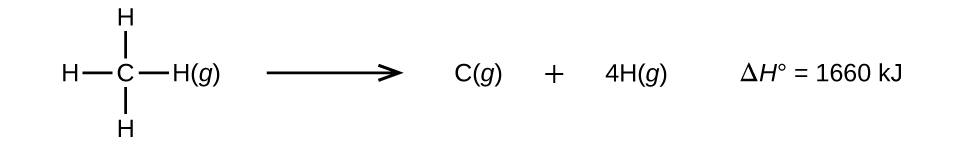
L’énergie moyenne de la liaison C-H, \(D_{C-H}\), est de 1660/4 = 415 kJ/mol parce qu’il y a quatre moles de liaisons C-H brisées par mole de la réaction. Bien que les quatre liaisons C-H soient équivalentes dans la molécule d’origine, elles ne nécessitent pas toutes la même énergie pour être rompues ; une fois la première liaison rompue (qui nécessite 439 kJ/mol), les autres liaisons sont plus faciles à rompre. La valeur de 415 kJ/mol est la moyenne, et non la valeur exacte requise pour rompre une quelconque liaison.
La force d’une liaison entre deux atomes augmente lorsque le nombre de paires d’électrons dans la liaison augmente. En général, lorsque la force de la liaison augmente, la longueur de la liaison diminue. Ainsi, on constate que les liaisons triples sont plus fortes et plus courtes que les liaisons doubles entre les deux mêmes atomes ; de même, les liaisons doubles sont plus fortes et plus courtes que les liaisons simples entre les deux mêmes atomes. Les énergies de liaison moyennes pour certaines liaisons courantes figurent dans le tableau \(\PageIndex{2}\), et une comparaison des longueurs et des forces de liaison pour certaines liaisons courantes figure dans le tableau \(\PageIndex{2}\). Lorsqu’un atome se lie à plusieurs atomes d’un groupe, la force de la liaison diminue généralement à mesure que l’on descend dans le groupe. Par exemple, C-F est de 439 kJ/mol, C-Cl de 330 kJ/mol et C-Br de 275 kJ/mol.
| La liaison | L’énergie de liaison | La liaison | L’énergie de liaison | La liaison | L’énergie de liaison | ||
|---|---|---|---|---|---|---|---|
| H-H | 436 | C-S | 260 | F-Cl | 255 | ||
| H-C | 415 | C-Cl | 330 | F-Br | 235 | ||
| H-N | 390 | C-Br | 275 | Si-Si | 230 | ||
| H-O | 464 | C-I | 240 | Si-P | 215 | ||
| H-F | 569 | N-N | 160 | Si-S | 225 | ||
| H-Si | 395 | \(\mathrm{N=N}\) | 418 | Si-Cl | 359 | ||
| H-P | 320 | \(\mathrm{N≡N}\) | 946 | Si-Br | 290 | ||
| H-S | 340 | N-O | 200 | Si-I | 215 | ||
| H-Cl | 432 | N-F | 270 | P-P | 215 | ||
| H-Br | 370 | N-P | 210 | P-S | 230 | ||
| H-I | 295 | N-Cl | 200 | P-Cl | 330 | ||
| C-C | 345 | N-Br | 245 | P-Br | 270 | ||
| \(\mathrm{C=C}\) | 611 | O-O | 140 | P-I | 215 | ||
| \(\mathrm{C≡C}\) | (\mathrm{O=O}\) | 498 | S-S | 215 | |||
| C-N | 290 | O-F | 160 | S-Cl | 250 | ||
| \(\mathrm{C=N}\) | 615 | O-Si | 370 | S-Br | 215 | ||
| \N(\mathrm{C≡N}\) | 891 | O-P | 350 | Cl-Cl | 243 | ||
| C-O | 350 | O-Cl | 205 | Cl-Br | 220 | ||
| \(\mathrm{C=O}\) | 741 | O-I | 200 | Cl-I | 210 | ||
| \(\mathrm{C≡O}\) | 1080 | F-F | 160 | Br-Br | 190 | ||
| C-F | 439 | F-Si | 540 | Br-I | 180 | ||
| C-Si | 360 | F-P | 489 | I-I | 150 | ||
| C-P | 265 | F-S | 285 |
| La liaison | La longueur de liaison (Å) | L’énergie de liaison (kJ/mol) |
|---|---|---|
| C-C | 1.54 | 345 |
| \(\mathrm{C=C}\) | 1.34 | 611 |
| \(\mathrm{C≡C}\) | 1.20 | 837 |
| C-N | 1.43 | 290 |
| (\mathrm{C=N}\) | 1.38 | 615 |
| \(\mathrm{C≡N}\) | 1.16 | 891 |
| C-O | 1.43 | 350 |
| (\mathrm{C=O}\) | 1.23 | 741 |
| \(\mathrm{C≡O}\) | 1,13 | 1080 |
Nous pouvons utiliser les énergies de liaison pour calculer les changements approximatifs d’enthalpie pour les réactions où les enthalpies de formation ne sont pas disponibles. Les calculs de ce type nous permettront également de savoir si une réaction est exothermique ou endothermique.
- Une réaction exothermique (ΔH négatif, chaleur produite) se produit lorsque les liaisons des produits sont plus fortes que celles des réactifs.
- Une réaction endothermique (ΔH positif, chaleur absorbée) se produit lorsque les liaisons des produits sont plus faibles que celles des réactifs.
Le changement d’enthalpie, ΔH, pour une réaction chimique est approximativement égal à la somme de l’énergie requise pour briser toutes les liaisons dans les réactifs (énergie « in », signe positif) plus l’énergie libérée lorsque toutes les liaisons sont formées dans les produits (énergie « out », signe négatif). On peut l’exprimer mathématiquement de la manière suivante :
\
Dans cette expression, le symbole \(\Sigma\) signifie « la somme de » et D représente l’énergie de liaison en kilojoules par mole, qui est toujours un nombre positif. L’énergie de liaison est obtenue à partir d’un tableau et dépend du fait que la liaison particulière est une liaison simple, double ou triple. Ainsi, en calculant les enthalpies de cette manière, il est important de prendre en compte la liaison dans tous les réactifs et produits. Comme les valeurs de D sont généralement des moyennes pour un type de liaison dans de nombreuses molécules différentes, ce calcul fournit une estimation approximative, et non une valeur exacte, de l’enthalpie de réaction.
Considérez la réaction suivante :
ou
\
Pour former deux moles de HCl, une mole de liaisons H-H et une mole de liaisons Cl-Cl doivent être brisées. L’énergie nécessaire à la rupture de ces liaisons est la somme de l’énergie de liaison de la liaison H-H (436 kJ/mol) et de la liaison Cl-Cl (243 kJ/mol). Au cours de la réaction, deux moles de liaisons H-Cl sont formées (énergie de liaison = 432 kJ/mol), libérant 2 × 432 kJ ; soit 864 kJ. Comme les liaisons des produits sont plus fortes que celles des réactifs, la réaction libère plus d’énergie qu’elle n’en consomme :
\-2D_{H-Cl}}\\\
&=\mathrm{-2(432)=-185\:kJ}
\end {align*}\]
Cet excès d’énergie est libéré sous forme de chaleur, la réaction est donc exothermique. Le tableau T2 donne une valeur pour l’enthalpie molaire standard de formation de HCl(g), \(ΔH^\circ_\ce f\), de -92,307 kJ/mol. Deux fois cette valeur est de -184,6 kJ, ce qui correspond bien à la réponse obtenue précédemment pour la formation de deux moles de HCl.
Exemple \(\PageIndex{1}\) : Utilisation des énergies de liaison pour approcher les changements d’enthalpie
Le méthanol, CH3OH, peut être un excellent carburant alternatif. La réaction à haute température de la vapeur et du carbone produit un mélange de gaz de monoxyde de carbone, CO, et d’hydrogène, H2, à partir duquel le méthanol peut être produit. En utilisant les énergies de liaison du tableau \(\PageIndex{2}\), calculez le changement approximatif d’enthalpie, ΔH, pour la réaction ici:
\
Solution
D’abord, nous devons écrire les structures de Lewis des réactifs et des produits:
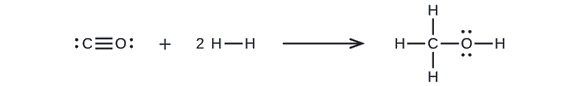
À partir de là, nous voyons que ΔH pour cette réaction implique l’énergie requise pour briser une triple liaison C-O et deux liaisons simples H-H, ainsi que l’énergie produite par la formation de trois liaisons simples C-H, une liaison simple C-O et une liaison simple O-H. Nous pouvons exprimer cela comme suit (via l’équation \ref{EQ3}):
\-}
\end {align*}\]
En utilisant les valeurs d’énergie de liaison dans le tableau \(\PageIndex{2}\), nous obtenons:
\end {align*}\]
Nous pouvons comparer cette valeur à celle calculée sur la base des données \(ΔH^\circ_\ce f\) de l’annexe G:
\end {align*}\]
Notez qu’il existe un écart assez important entre les valeurs calculées par les deux méthodes différentes. Cela se produit parce que les valeurs D sont la moyenne de différentes forces de liaison ; par conséquent, elles ne donnent souvent qu’un accord approximatif avec d’autres données.
Exercice \(\PageIndex{1}\)
L’alcool éthylique, CH3CH2OH, a été l’un des premiers produits chimiques organiques délibérément synthétisés par l’homme. Il a de nombreuses utilisations dans l’industrie, et c’est l’alcool contenu dans les boissons alcoolisées. Il peut être obtenu par la fermentation du sucre ou synthétisé par l’hydratation de l’éthylène dans la réaction suivante :

En utilisant les énergies de liaison du tableau \(\PageIndex{2}\), calculez un changement d’enthalpie approximatif, ΔH, pour cette réaction.
Résumé
Vidéo \(\PageIndex{2}\) : Un examen de la liaison atomique.
Les liaisons covalentes se forment lorsque les électrons sont partagés entre les atomes et sont attirés par les noyaux des deux atomes. Dans les liaisons covalentes pures, les électrons sont partagés de manière égale. Dans les liaisons covalentes polaires, les électrons sont partagés de manière inégale, car un atome exerce une force d’attraction plus forte sur les électrons que l’autre.
La force d’une liaison covalente est mesurée par son énergie de dissociation de la liaison, c’est-à-dire la quantité d’énergie nécessaire pour rompre cette liaison particulière dans une mole de molécules. Les liaisons multiples sont plus fortes que les liaisons simples entre les mêmes atomes. L’enthalpie d’une réaction peut être estimée en fonction de l’apport d’énergie nécessaire à la rupture des liaisons et de l’énergie libérée lorsque de nouvelles liaisons sont formées.
Équations clés
- Énergie de liaison pour une molécule diatomique : \(\ce{XY}(g)⟶\ce{X}(g)+\ce{Y}(g)\hspace{20px}\ce{D_{X–Y}}=ΔH°\)
- Enthalpy change: ΔH = ƩLiens brisés – ƩLiens formés
Notes de bas de page
- Cette question est tirée de l’examen de placement avancé en chimie et est utilisée avec la permission de l’Educational Testing Service.
Glossaire
énergie de liaison (également, énergie de dissociation de la liaison) énergie requise pour rompre une liaison covalente dans une substance gazeuse
Contributeurs
-
Paul Flowers (Université de Caroline du Nord – Pembroke), Klaus Theopold (Université du Delaware) et Richard Langley (Université d’État de Stephen F. Austin State University) avec des auteurs collaborateurs. Le contenu des manuels scolaires produit par OpenStax College est sous licence Creative Commons Attribution License 4.0. Télécharger gratuitement à http://cnx.org/contents/85abf193-2bd…[email protected]).
- Adelaide Clark, Oregon Institute of Technology
- Fuse School, ressource éducative ouverte gratuite, sous une licence Creative Commons : Attribution-NonCommercial CC BY-NC (Voir acte de licence : https://creativecommons.org/licenses/by-nc/4.0/)
- Crash Course Chemistry : Crash Course est une division de Complexly et les vidéos sont libres d’être diffusées en continu à des fins éducatives.
Réaction
Vous avez une réaction à donner sur ce texte ? Cliquez ici.
Vous avez trouvé une coquille et vous voulez un crédit supplémentaire ? Cliquez ici.