Autoencodeurs convolutifs pour la réduction du bruit des images

Dans « Anomaly Detection with Autoencoders Made Easy » j’ai mentionné que les autoencodeurs ont été largement appliqués dans la réduction de dimension et la réduction du bruit des images. Depuis lors, de nombreux lecteurs m’ont demandé si je pouvais couvrir le sujet de la réduction du bruit des images à l’aide d’autoencodeurs. C’est la motivation de ce post.

La modélisation des données d’image nécessite une approche spéciale dans le monde des réseaux neuronaux. Le réseau de neurones le plus connu pour la modélisation des données d’image est le réseau de neurones convolutif (CNN, ou ConvNet) ou appelé autoencodeur convolutif. Dans ce billet, je commencerai par une introduction aux données d’image, car tous les lecteurs ne sont pas spécialisés dans ce domaine (n’hésitez pas à sauter cette section si vous êtes déjà familiarisé avec). Je décrirai ensuite un réseau neuronal standard simple pour les données d’image. Cela me donnera l’occasion de démontrer pourquoi les auto-encodeurs convolutifs sont la méthode préférée pour traiter les données d’image. Surtout, je montrerai comment les auto-encodeurs convolutifs réduisent les bruits dans une image. J’utilise le module Keras et les données MNIST dans ce billet. Le carnet de notes est disponible via ce lien. Keras est une API de réseaux neuronaux de haut niveau, écrite en Python et capable de fonctionner au-dessus de TensorFlow. Ce billet est une extension de mon billet précédent « Qu’est-ce que la reconnaissance d’images ? » que je vous encourage à regarder.

J’ai pensé qu’il est utile de mentionner les trois grandes catégories de données. Les trois catégories de données sont : (1) les données non corrélées (par opposition aux données en série), (2) les données en série (y compris les données de texte et de flux vocal) et (3) les données d’image. L’apprentissage profond comporte trois variantes de base pour traiter chaque catégorie de données : (1) le réseau neuronal feedforward standard, (2) RNN/LSTM, et (3) CNN (Convolutional NN). Les lecteurs qui recherchent des didacticiels pour chaque type sont invités à consulter l’article « Explaining Deep Learning in a Regression-Friendly Way » (1), l’article actuel « A Technical Guide for RNN/LSTM/GRU on Stock Price Prediction » (2), et les articles « Deep Learning with PyTorch Is Not Torturing », « What Is Image Recognition ? », « Anomaly Detection with Autoencoders Made Easy » et « Convolutional Autoencoders for Image Noise Reduction » (3). Vous pouvez mettre en signet l’article récapitulatif « Dataman Learning Paths – Build Your Skills, Drive Your Career ».

Understand Image Data

Une image est constituée de « pixels » comme le montre la figure (A). Dans une image en noir et blanc, chaque pixel est représenté par un nombre allant de 0 à 255. Aujourd’hui, la plupart des images utilisent une couleur de 24 bits ou plus. Une image en couleur RVB signifie que la couleur d’un pixel est la combinaison du rouge, du vert et du bleu, chacune de ces couleurs allant de 0 à 255. Le système de couleurs RVB construit toutes les couleurs à partir de la combinaison des couleurs rouge, verte et bleue, comme le montre ce générateur de couleurs RVB. Ainsi, un pixel contient un ensemble de trois valeurs RVB(102, 255, 102) fait référence à la couleur #66ff66.

Une image de 800 pixels de large, 600 pixels de haut a 800 x 600 = 480 000 pixels = 0,48 mégapixels (« mégapixel » correspond à 1 million de pixels). Une image d’une résolution de 1024×768 est une grille de 1 024 colonnes et 768 lignes, qui contient donc 1 024 × 768 = 0,78 mégapixels.

MNIST

La base de données MNIST (Modified National Institute of Standards and Technology database) est une grande base de données de chiffres manuscrits qui est couramment utilisée pour l’entraînement de divers systèmes de traitement d’images. L’ensemble de données d’entraînement dans Keras a 60 000 enregistrements et l’ensemble de données de test a 10 000 enregistrements. Chaque enregistrement a 28 x 28 pixels.

À quoi ressemblent-ils ? Utilisons matplotlib et sa fonction image imshow() pour afficher les dix premiers enregistrements.

Empile les données d’image pour l’entraînement

Afin d’adapter un cadre de réseau neuronal pour l’entraînement du modèle, nous pouvons empiler toutes les 28 x 28 = 784 valeurs dans une colonne. La colonne empilée pour le premier enregistrement ressemble à ceci : (en utilisant x_train.reshape(1,784)):

Puis nous pouvons entraîner le modèle avec un réseau neuronal standard, comme le montre la figure (B). Chacune des 784 valeurs est un nœud dans la couche d’entrée. Mais attendez, n’avons-nous pas perdu beaucoup d’informations en empilant les données ? Oui. Les relations spatiales et temporelles dans une image ont été écartées. Il s’agit d’une grande perte d’informations. Voyons comment les auto-codeurs convolutifs peuvent conserver les informations spatiales et temporelles.

Pourquoi les auto-codeurs convolutifs conviennent-ils aux données d’image ?

Nous constatons une énorme perte d’informations lorsque nous tranchons et empilons les données. Au lieu d’empiler les données, les auto-codeurs convolutifs gardent les informations spatiales des données d’image d’entrée telles quelles, et extraient les informations en douceur dans ce qu’on appelle la couche de convolution. La figure (D) montre qu’une image 2D plate est extraite en un carré épais (Conv1), puis continue pour devenir un long cube (Conv2) et un autre cube plus long (Conv3). Ce processus est conçu pour conserver les relations spatiales dans les données. C’est le processus d’encodage dans un Autoencodeur. Au milieu, on trouve un auto-codeur entièrement connecté dont la couche cachée est composée de seulement 10 neurones. Vient ensuite le processus de décodage qui aplatit les cubes, puis en une image plane en 2D. L’encodeur et le décodeur sont symétriques dans la figure (D). Ils n’ont pas besoin d’être symétriques, mais la plupart des praticiens adoptent simplement cette règle comme expliqué dans « Anomaly Detection with Autoencoders made easy ».

Comment fonctionnent les autoencodeurs convolutifs ?

L’extraction de données ci-dessus semble magique. Comment cela fonctionne-t-il réellement ? Elle fait intervenir les trois couches suivantes : La couche de convolution, la couche reLu et la couche de mise en commun.

1. La couche de convolution

L’étape de convolution crée de nombreux petits morceaux appelés cartes de caractéristiques ou caractéristiques comme les carrés verts, rouges ou bleu marine de la figure (E). Ces carrés préservent la relation entre les pixels de l’image d’entrée. Laissez chaque caractéristique balayer l’image d’origine comme le montre la figure (F). Ce processus de production des scores est appelé filtrage.

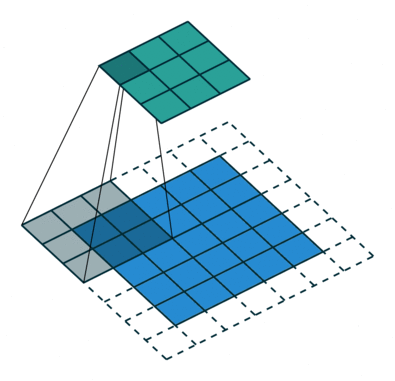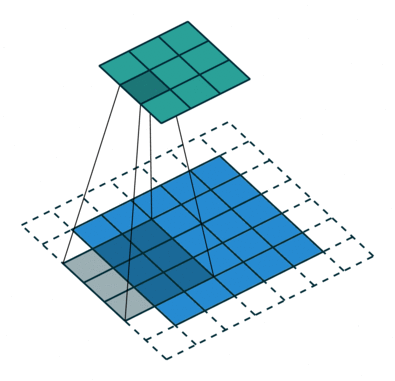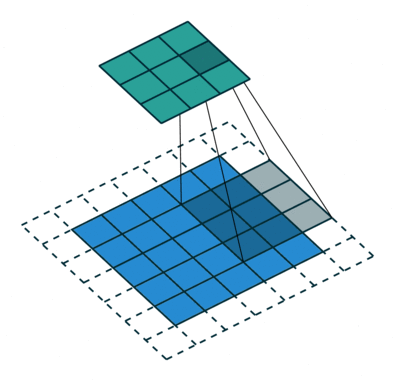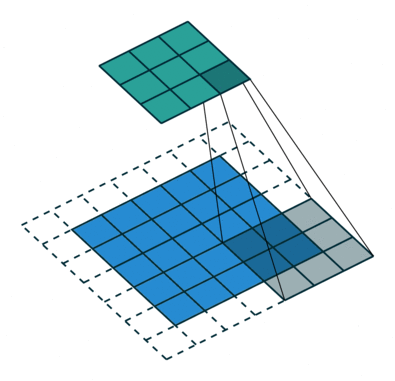
Après avoir balayé l’image originale, chaque caractéristique produit une image filtrée avec des scores élevés et des scores faibles, comme le montre la figure (G). S’il y a une correspondance parfaite, il y a un score élevé dans cette case. S’il y a une faible correspondance ou aucune correspondance, le score est faible ou nul. Par exemple, le carré rouge a trouvé quatre zones dans l’image originale qui montrent une correspondance parfaite avec la caractéristique, donc les scores sont élevés pour ces quatre zones.

Plus de filtres signifient plus de nombre de caractéristiques que le modèle peut extraire. Cependant, plus de caractéristiques signifie un temps de formation plus long. Il est donc conseillé d’utiliser le nombre minimum de filtres pour extraire les caractéristiques.

1.1 Padding

Comment les caractéristiques déterminent-elles la correspondance ? Un hyperparamètre est Padding qui offre deux options : (i) rembourrer l’image originale avec des zéros afin de correspondre à la caractéristique, ou (ii) laisser tomber la partie de l’image originale qui ne correspond pas et garder la partie valide.

1.2 Strides

La couche de convolution comprend un autre paramètre : le Stride. Il s’agit du nombre de pixels se déplaçant sur la matrice d’entrée. Lorsque le stride est égal à 1, les filtres se décalent de 1 pixel à la fois. Nous le verrons dans notre code Keras comme un hyper-paramètre.

2. Étape ReLUs

L’unité linéaire rectifiée (ReLU) est l’étape qui est la même que celle des réseaux neuronaux typiques. Elle rectifie toute valeur négative à zéro afin de garantir que les mathématiques se comportent correctement.

3. Couche de mise en commun maximale

La mise en commun réduit la taille de l’image. Dans la figure (H), une fenêtre 2 x 2, appelée taille du pool, parcourt chacune des images filtrées et attribue la valeur maximale de cette fenêtre 2 x 2 à un carré 1 x 1 dans une nouvelle image. Comme illustré sur la figure (H), la valeur maximale de la première fenêtre 2 x 2 est un score élevé (représenté par le rouge), donc le score élevé est attribué au carré 1 x 1.

En dehors de la prise de la valeur maximale, d’autres méthodes de pooling moins courantes incluent le Average Pooling (prise de la valeur moyenne) ou le Sum Pooling (la somme).

Après le pooling, une nouvelle pile d’images filtrées plus petites est produite. Maintenant, nous divisons les images filtrées plus petites et les empilons dans une liste comme indiqué sur la figure (J).

Modèle dans Keras

Les trois couches ci-dessus sont les blocs de construction dans le réseau neuronal à convolution. Keras offre les deux fonctions suivantes :

Vous pouvez construire de nombreuses couches de convolution dans les autoencodeurs de convolution. Dans la figure (E), il y a trois couches étiquetées Conv1, Conv2 et Conv3 dans la partie encodage. Nous allons donc construire en conséquence.

• Le code ci-dessous input_img = Input(shape=(28,28,1) déclare que l’image 2D d’entrée est 28 par 28.
• Puis il construit les trois couches Conv1, Conv2 et Conv3.
• Notez que Conv1 est à l’intérieur de Conv2 et Conv2 est à l’intérieur de Conv3.
• Le padding spécifie ce qu’il faut faire lorsque le filtre ne s’adapte pas bien à l’image d’entrée. padding='valid' signifie laisser tomber la partie de l’image quand le filtre ne s’adapte pas ; padding='same' tamponne l’image avec des zéros pour s’adapter à l’image.

Puis il continue à ajouter le processus de décodage. Ainsi, la partie decode ci-dessous a tout le codage et le décodage.

L’api Keras requiert la déclaration du modèle et de la méthode d’optimisation:

• Model(inputs= input_img,outputs= decoded) : Le modèle comprendra toutes les couches nécessaires au calcul des sorties decoded étant donné les données d’entrée input_img. compile(optimizer='adadelta',loss='binary_crossentropy') : L’optimiseur effectue une optimisation comme le fait le gradient decent. Les plus courants sont le gradient décent stochastique (SGD), le gradient adapté (Adagrad), et Adadelta qui est une extension d’Adagrad. Consultez la documentation de l’optimiseur Keras pour plus de détails. Les fonctions de perte peuvent être trouvées dans la documentation des pertes de Keras.

Ci-après, je forme le modèle en utilisant x_train comme entrée et sortie. Le batch_size est le nombre d’échantillons et le epoch est le nombre d’itérations. Je spécifie shuffle=True pour exiger le brassage des données d’entraînement avant chaque époque.

Nous pouvons imprimer les dix premières images originales et les prédictions pour ces mêmes dix images.

Comment construire un auto-codeur à convolution de réduction du bruit d’image?

L’idée de la réduction du bruit d’image est d’entraîner un modèle avec des données bruitées comme entrées, et leurs données claires respectives comme sorties. C’est la seule différence avec le modèle ci-dessus. Commençons par ajouter des bruits aux données.

Les dix premières images bruitées ressemblent à ce qui suit :

Puis nous entraînons le modèle avec les données bruitées comme entrées, et les données propres comme sorties.

Enfin, nous imprimons les dix premières images bruitées ainsi que les images débruitées correspondantes.

Le carnet de notes est disponible via ce lien.

Y a-t-il un code de CNN pré-entraînés que je peux utiliser ?

Oui. Si vous êtes intéressé par l’apprentissage du code, Keras dispose de plusieurs CNN pré-entraînés, notamment Xception, VGG16, VGG19, ResNet50, InceptionV3, InceptionResNetV2, MobileNet, DenseNet, NASNet et MobileNetV2. Il convient de mentionner cette grande base de données d’images ImageNet que vous pouvez contribuer ou télécharger à des fins de recherche.