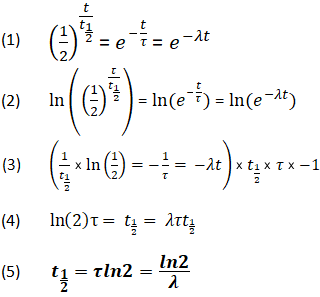Les outils suivants peuvent générer n’importe laquelle des valeurs à partir des trois autres dans la formule de demi-vie pour une substance subissant une désintégration pour diminuer de moitié.

Calculateur de demi-vie
Veuillez fournir l’un des trois éléments suivants pour calculer la quatrième valeur.
Conversion de la demi-vie, de la durée de vie moyenne et de la constante de désintégration
Veuillez fournir l’un des éléments suivants pour obtenir les deux autres.
Définition et formule
La demi-vie est définie comme le temps nécessaire à une quantité donnée pour diminuer de moitié par rapport à sa valeur initiale. Le terme est le plus souvent utilisé en relation avec les atomes subissant une désintégration radioactive, mais il peut être utilisé pour décrire d’autres types de désintégration, exponentielle ou non. L’une des applications les plus connues de la demi-vie est la datation au carbone 14. La demi-vie du carbone 14 est d’environ 5 730 ans et peut être utilisée de manière fiable pour mesurer des dates allant jusqu’à environ 50 000 ans. Le processus de datation au carbone 14 a été mis au point par William Libby et repose sur le fait que le carbone 14 est constamment produit dans l’atmosphère. Il est incorporé aux plantes par la photosynthèse, puis aux animaux lorsqu’ils consomment des plantes. Le carbone-14 subit une désintégration radioactive une fois que la plante ou l’animal meurt, et la mesure de la quantité de carbone-14 dans un échantillon transmet des informations sur le moment où la plante ou l’animal est mort.
Vous trouverez ci-dessous trois formules équivalentes décrivant la décroissance exponentielle :
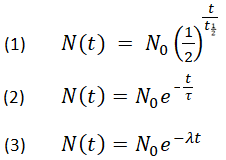
- où
N0 est la quantité initiale
Nt est la quantité restante après le temps, t
t1/2 est la demi-vie
τ est la durée de vie moyenne
λ est la constante de désintégration
Si un archéologue trouve un échantillon fossile qui contient 25% de carbone 14 par rapport à un échantillon vivant, le moment de la mort de l’échantillon fossile pourrait être déterminé en réarrangeant l’équation 1, puisque Nt, N0, et t1/2 sont connus.
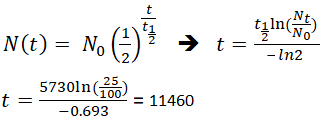
Cela signifie que le fossile a 11 460 ans.
Dérivation de la relation entre les constantes de demi-vie
En utilisant les équations ci-dessus, il est également possible de dériver une relation entre t1/2, τ, et λ. Cette relation permet de déterminer toutes les valeurs, tant qu’au moins une est connue.